Documenti di Didattica
Documenti di Professioni
Documenti di Cultura
2 Calculo Diferencial en Varias Variables
Caricato da
Milena Tvr BustosTitolo originale
Copyright
Formati disponibili
Condividi questo documento
Condividi o incorpora il documento
Hai trovato utile questo documento?
Questo contenuto è inappropriato?
Segnala questo documentoCopyright:
Formati disponibili
2 Calculo Diferencial en Varias Variables
Caricato da
Milena Tvr BustosCopyright:
Formati disponibili
Clculo en Varias Variables
Captulo 2: Clculo Diferencial en
Varias Variables
Instituto de Matemtica
Universidad Austral de Chile
1
2.1 Derivadas Parciales. Diferenciabilidad
2
Derivadas Parciales :
: ,
n
f D D
abierto
( )
( ) ( )
1 2 1 2
1 2
0
, ,..., ,..., , ,...,
, ,..., lim
j n n
n
h
j
f x x x h x f x x x
f
x x x
x h
0
( ) ( )
lim
j
h
f x he f x
h
Si el lmite existe, se llama DERIVADA PARCIAL de
f
respecto de
j
x
.
Instituto de Matemtica
Universidad Austral de Chile
En particular:
-Para
2
2
: f D
( )
( ) ( )
0
, ,
, lim
o o o o
o o
h
f x h y f x y
f
x y
x h
( )
( ) ( )
0
, ,
, lim
o o o o
o o
h
f x y h f x y
f
x y
y h
2.1 Derivadas Parciales. Diferenciabilidad
3
Instituto de Matemtica
Universidad Austral de Chile
-Para
3
3
: f D
( )
( ) ( )
0
, , , ,
, , lim
o o o o o o
o o o
h
f x h y z f x y z
f
x y z
x h
Anlogo para
( )
, ,
o o o
f
x y z
y
,
( )
, ,
o o o
f
x y z
z
Notaciones:
1 x x
f z
f f z
x x
2 y y
f z
f f z
y y
Para :
n m
F A
1 2
( , ,..., )
m
F F F F
Se puede calcular:
, 1,..., ;
i
j
F
i m
x
1,..., . j n
Observaciones:
En general, para calcular
i
f
x
, se deriva
f
respecto de
i
x
considerando constantes las otras variables.
2.1 Derivadas Parciales. Diferenciabilidad
4
Instituto de Matemtica
Universidad Austral de Chile
Interpretacin Geomtrica para n=2:
( , )
o o
f
x y
x
Pendiente de la recta tangente a la traza del grfico de
f
respecto del plano
o
y y
.
( , )
o o
f
x y
y
Pendiente de la recta tangente a la traza del grfico de
f
respecto del plano
o
x x
.
2.1 Derivadas Parciales. Diferenciabilidad
5
Instituto de Matemtica
Universidad Austral de Chile
Observaciones:
-En una variable se tena que:
f
es diferenciable (derivable) en
o
x
si existe derivada de
f
en
o
x
.
( ) ( )
o
f x
- En varias variables no es suficiente la existencia de las derivadas parciales en un
punto
( )
,
o o
x y
para decir que
f
es diferenciable en ese punto, pues no se cumpliran
muchos resultados usuales, como la REGLA DE LA CADENA.
Por ejemplo : Sean
1 1
3 3
( , ) f x y x y
( ) ( , ) g x x x
As:
( ) ( )
1 1 2
3 3 3
( ) ( ) ( , ) f g x f g x f x x x x x
Se cumple :
f
tiene derivadas parciales en
( )
0,0
,pues:
1
3
0 0
( ,0) (0,0) 0 0
(0,0) lim lim 0
h h
f f h f h
x h h
1
3
0 0
(0, ) (0,0) 0 0
(0,0) lim lim 0
h h
f f h f h
y h h
2.1 Derivadas Parciales. Diferenciabilidad
6
Instituto de Matemtica
Universidad Austral de Chile
g
tiene derivada en 0,pues:
( ) (1,1) g x
As:
(0) (1,1) g
Pero:
f g
no tiene derivada en 0, pues:
( )
( ) ( )
0
( ) (0)
(0) lim
h
f g h f g
f g
h
2
3
0
0
lim
h
h
h
1
0
3
1
lim
h
h
NO EXISTE.
2.1 Derivadas Parciales. Diferenciabilidad
7
Instituto de Matemtica
Universidad Austral de Chile
-As la diferenciabilidad de una funcin de varias variables no es equivalente a la existencia de
las derivadas parciales.
-Para
f
funcin de 2 variables, geomtricamente
f
ser DIFERENCIABLE en
( )
,
o o
x y
si
existe PLANO TANGENTE al grfico de
f
en el punto
( )
, , ( , )
o o o o
x y f x y
y esto ocurre si
f
es suave en ese punto, o sea su grfico no tiene vrtices, puntos, aristas, etc., a ll.
-Obtengamos intuitivamente la ecuacin del plano tangente a
( , ) z f x y
en
( , )
o o
x y
.
Sea
z ax by c + +
la ecuacin del plano tangente.
Para las trazas
o
x x ,
o
y y
las pendientes de las rectas tangentes deben ser:
( , ),
o o
f
x y
y
( )
,
o o
f
x y
x
respectivamente.
,
z
a
x
z
b
y
( , ), ( , )
o o o o
f f
a x y b x y
x y
2.1 Derivadas Parciales. Diferenciabilidad
8
Instituto de Matemtica
Universidad Austral de Chile
Adems:
( , ) ( , )
o o o o
z x y f x y
As:
( , )
o o o o
ax by c f x y + +
( , ) ( , ) ( , )
o o o o o o o o
f f
c f x y x y x x y y
x y
As la ecuacin del plano tangente ser:
( , ) ( , ) ( , ) ( , ) ( , )
o o o o o o o o o o o o
f f f f
z x y x x y y f x y x y x x y y
x y x y
+ +
O sea:
( , ) ( , )( ) ( , )( )
o o o o o o o o
f f
z f x y x y x x x y y y
x y
+ +
2.1 Derivadas Parciales. Diferenciabilidad
9
Instituto de Matemtica
Universidad Austral de Chile
Definicin de Diferenciabilidad en 2 Variables :
2
: , f D Dabierto,
( , )
o o
x y D
f
es DIFERENCIABLE en
( , )
o o
x y
si:
( , ),
o o
f
x y
x
( , )
o o
f
x y
y
existen y adems:
( , ) ( , )
( , ) ( , ) ( , )( ) ( , )( )
lim 0
( , ) ( , ) o o
o o o o o o o o
x y x y
o o
f f
f x y f x y x y x x x y y y
x y
x y x y
2.1 Derivadas Parciales. Diferenciabilidad
10
Instituto de Matemtica
Universidad Austral de Chile
: ,
n m
F D Dabierto,
1
( ,..., )
m
F F F
;
F
es DIFERENCIABLE en
o x D si:
1)Existen derivadas parciales
( ), 1,...,
i
o
j
F
x i m
x
1,..., j n
2)
( ) ( ) ( )( )
lim 0
o
o o o
x x
o
F x F x DF x x x
x x
1 1 1
1 2
2 2 2
1 2
1 2
...
...
:
... ... ...
...
n
n
m m m
n
F F F
x x x
F F F
x x x donde DF
F F F
x x x
1
1
1
1
1
1
1
1
1
1
]
Diferenciabilidad para Fde
n
a
m
:
2.1 Derivadas Parciales. Diferenciabilidad
11
Instituto de Matemtica
Universidad Austral de Chile
Se llama MATRIZ JACOBIANA de F
y es la DERIVADA deF.
(
o
x x se considera como matriz columna y
( ) ( ) o o DF x x x
es el producto de una matriz m n por otra 1 n ).
Sea
:
n
f D
, Dabierto,
f
diferenciable.
La Derivada de
f
es una matriz 1 n .
1 2
...
n
f f f
Df
x x x
1
1
]
que puede expresarse como vector de
n
.
1 2
, ,...,
n
f f f
Df
x x x
_
,
se llama VECTOR GRADIENTE de
f
y se anota:
( ) grad f
f
Gradiente:
2.1 Derivadas Parciales. Diferenciabilidad
12
Instituto de Matemtica
Universidad Austral de Chile
Teorema :
:
n m
F D
1) Fdiferenciable en
o x F
continua en
o x
.
2) Existen todas las derivadas parciales de Fy son continuas en
o x
F es diferenciable en
o x .
Observaciones:
1) Los recprocos no son verdaderos.
2) Una funcin que tiene derivadas parciales continuas se dice de clase
1
C .
3) Se cumple la siguiente relacin:
Derivadas
Parciales
Continuas
Diferenciable
Existen
Derivadas
Parciales
Teorema (2)
Definicin
2.1 Derivadas Parciales. Diferenciabilidad
13
Instituto de Matemtica
Universidad Austral de Chile
Ejemplos:
1)
2
: f
1, 0 0
( , )
0, en otro caso
x y
f x y
'
0
( ,0) (0,0)
(0,0) lim 0
h
f f h f
x h
0
(0, ) (0,0)
(0,0) lim 0
h
f f h f
y h
f
no es continua en
( )
0,0
pues:
1.
( )
0,0 1 f
2.
( , ) (0,0)
lim ( , )
x y
f x y
no existe, pues por el eje X y el eje Y los lmites resultan 1, y
por cualquier otra trayectoria da 0.
f
no es diferenciable en
( )
0,0
.
2.1 Derivadas Parciales. Diferenciabilidad
14
Instituto de Matemtica
Universidad Austral de Chile
En este ejemplo se ve que la existencia de las derivadas parciales en un punto no asegura
la diferenciabilidad all.
2) 2 2
,( , ) (0,0)
( , )
0, ( , ) (0,0)
xy
x y
f x y x y
x y
+
'
0 0
( ,0) (0,0) 0 0
(0,0) lim lim 0
h h
f f h f
x h h
0 0
(0, ) (0,0) 0 0
(0,0) lim lim 0
h h
f f h f
y h h
2.1 Derivadas Parciales. Diferenciabilidad
15
Instituto de Matemtica
Universidad Austral de Chile
f
x
no es continua en
( )
0,0
pues:
3
3
2 2
,( , ) (0,0)
( , )
0, ( , ) (0,0)
y
x y
f
x y
x y
x
x y
' +
3
3
( , ) (0,0) ( , ) (0,0)
2 2
lim ( , ) lim
x y x y
f y
x y
x
x y
+
NO EXISTE
2.1 Derivadas Parciales. Diferenciabilidad
16
Instituto de Matemtica
Universidad Austral de Chile
En este ejemplo se ve que la existencia de las derivadas parciales en un punto no asegura
la continuidad de stas.
(Pues para la trayectoria:
0 y
resulta
( )
3
0
2
0
lim 0
x
x
Y para la trayectoria 0 x resulta
3
3
0
lim
y
y
y
, lmite que no existe,
pues por la izquierda vale -1 y por la derecha vale 1. )
2.2 Regla de la Cadena. Derivadas Direccionales
17
Instituto de Matemtica
Universidad Austral de Chile
Regla de la Cadena:
Sean
:
n m
g D
,
:
m p
f D
, DD abiertos
/ ( ) g D D
Se cumple:
g
diferenciable en
o
x
y
f
diferenciable en
( )
o
g x
f g
diferenciable en
o
x .
Adems:
( )( ) ( ( )) ( ) o o o D f g x Df g x Dg x
Casos Particulares :
1)
1, 2. n p m
2
: , g D
2
: f D
( ) ( ( ), ( )) g t x t y t
( , ) z f x y
: f g D
( ( ) ) g D D
As podemos escribir abreviadamente:
z z x z y
t x t y t
+
La relacin entre las variables se puede representar en un diagrama.
(Observar que para hallar la derivada de z respecto de t , se sigui 2 caminos desde z hasta t ).
2.2 Regla de la Cadena. Derivadas Direccionales
18
Instituto de Matemtica
Universidad Austral de Chile
( )( ) ( ( )) ( ( ), ( )) f g t f g t f x t y t
( )( ) ( ( )) ( )
o o o
D f g t Df g t Dg t
( ( ), ( )), ( ( ), ( )) ( ( ), ( ))
o o o o o o
f f
x t y t x t y t x t y t
x y
_
,
( ( ), ( )) ( ) ( ( ), ( )) ( )
o o o o o o
f f
x t y t x t x t y t y t
x y
+
2.2 Regla de la Cadena. Derivadas Direccionales
19
Instituto de Matemtica
Universidad Austral de Chile
2)
2, 3, 1. n m p
2 3
: , g D
3
: f D
( , ) ( , , ) g x y u v w
( , , ) s f u v w
2
: f g D
( )( ) ( ( )) ( ) o
o o
D f g x Df g x Dg x
, ,
u u
x y
f f f v v
u v w x y
w w
x y
1
1
1
1 _
1
,
1
1
1
]
f u f v f w f u f v f w
u x v x w x u y v y w y
1
+ + + +
1
]
s s
x y
1
1
]
2.2 Regla de la Cadena. Derivadas Direccionales
20
Instituto de Matemtica
Universidad Austral de Chile
Diagrama:
s s u s v s w
x u x v x w x
s s u s v s w
y u y v y w y
+ +
+ +
(En este caso, tambin se cumple que para calcular la derivada parcial de s respecto a
una variable
(x
) y
se sigui los 3 caminos que van desde s a la variable
(x
) y
).
Derivadas Direccionales:
:
n
f D
, ,
n
o
x Dv , Dabierto.
La Derivada Direccional de
f
en
o x en la direccin del vector ves:
0
( ) ( )
( ) lim
o o
o
v
h
f x hv f x
D f x
h
2.2 Regla de la Cadena. Derivadas Direccionales
21
Instituto de Matemtica
Universidad Austral de Chile
(Obs.: Generalmente se considera vvector unitario, o sea
1 v
.Si vno es unitario,
se normaliza dividiendo por el mdulo:
v
v
).
Interpretacin Geomtrica para n=2:
-
( , )
o o
v
D f x y
es la pendiente de la recta tangente a la curva que es traza de la
superficie con un plano vertical que pasa por
( , )
o o
x y
en direccin paralela a v.
-
( , )
o o
v
D f x y
es la razn de cambio de los valores de
f
a lo largo de la recta que pasa
por
( , )
o o
x y
y tiene la direccin v
.
2.2 Regla de la Cadena. Derivadas Direccionales
22
Instituto de Matemtica
Universidad Austral de Chile
Derivadas Direccionales y Gradiente:
Segn la definicin tenemos que:
0
( ) ( ) o o
v
t
d
D f x f x tv
dt
+
(Pues de acuerdo a la definicin de una funcin real de una variable,
0
0
( ) ( )
( ) lim
o o
o
h
t
d f x tv f x
f x tv
dt h
+
+
As para n=3
Si
3
: g
,
( ) o g t x tv +
Entonces
( ) ( )( ) o f x tv f g t +
Luego:
0
( ) ( ) o o
v
t
df
Df x x tv
dt
+
( )(0)
d
f g
dt
( (0)) (0) Df g Dg
( ) o f x v
As:
( ) ( ) o o
v
Df x f x v
(Anlogo para n=2)
2.2 Regla de la Cadena. Derivadas Direccionales
23
Instituto de Matemtica
Universidad Austral de Chile
Direccin de Mximo Crecimiento (Para n=2) :
( ) ( ) o o
v
Df x f x v
( ) cos o f x v
, ( ngulo entre
( ) o f x
y v ).
( ) cos o f x
, (Pues
1 v
).
As
( ) o
v
Df x
tendr valor mximo si cos 1 o sea si 0 , es decir si
( ) o f x
y
vtienen la misma direccin.
Luego:
La direccin de mximo crecimiento de una funcin
f
es en la direccin de
( ) o f x
y el valor mximo es
( )
o
f x
.
2.2 Regla de la Cadena. Derivadas Direccionales
24
Instituto de Matemtica
Universidad Austral de Chile
El Gradiente es Normal a las Superficies de Nivel (Para n=3):
3
: f D
, Dabierto,
f
de clase
1
. C
( , , )
o o o
x y z
un punto en una superficie de
nivel : c
{ }
2
( , , ) / ( , , ) S x y z f x y z c
Entonces:
( , , )
o o o
f x y z
es normal a la superficie Sen el siguiente sentido:
Si ves el vector tangente en 0 t de una trayectoria
( ) r t
en S, tal que
(0) ( , , )
o o o
r x y z
.
Entonces:
( , , ) 0
o o o
f x y z v
2.2 Regla de la Cadena. Derivadas Direccionales
25
Instituto de Matemtica
Universidad Austral de Chile
Demostracin:
( ) r t
trayectoria en S ( ( )) f r t c
Sea
(0) v r
0
( ( )) 0
t
d
f r t
dt
(Pues
( ( )) f r t c
constante)
( (0)) (0) 0 f r r
( , , ) 0
o o o
f x y z v
Plano Tangente para Superficie de N ivel:
Sea S la superficie de nivel c, de una funcin de 3 variables
( , , ) f x y z
O sea:
{ }
3
( , , ) / ( , , ) S x y z f x y z c
Sea
( , , )
o o o
x y z S
2.2 Regla de la Cadena. Derivadas Direccionales
26
Instituto de Matemtica
Universidad Austral de Chile
(Observaciones: Antes se haba dado la ecuacin del plano tangente a una superficie que es
grfica de una funcin de 2 variables
( , ) z f x y
).
Y era:
( , ) ( , ) ( , )
o o o o o o
f x y x x y y z f x y
El plano tangente a Sen
( , , )
o o o
x y z
es:
( , , ) ( , , ) 0
o o o o o o
f x y z x x y y z z
(Si
( , , ) 0
o o o
f x y z
)
2.3 Derivadas de Orden Superior. Teorema de Taylor
27
Instituto de Matemtica
Universidad Austral de Chile
Derivadas de Orden Superior:
- Sea
:
n
f D
, Dabierto,
f
de clase
1
, C o sea sus derivadas parciales existen
y son continuas.
- Si las derivadas parciales de las derivadas parciales (funciones) existen y son continuas, se
dice que
f
es de clase
2
C . Anlogamente para
3
,...,
n
C C .
Se dice que
f
es de clase C
si es de clase
n
C , . n
- Derivadas de 2 orden:
2
2
f f
x x x
_
,
,
2
f f
y x y x
_
,
2
f f
x y x y
_
,
,
2
2
f f
y y y
_
,
2.3 Derivadas de Orden Superior. Teorema de Taylor
28
Instituto de Matemtica
Universidad Austral de Chile
(Tambin se anotan:
, , ,
xx xy yx yy
f f f f
2 2 2 2
2 2
, , ,
z z z z
x y x x y y
, , ,
xx xy yx yy
z z z z
respectivamente).
- Derivadas de 3,4,,n orden se definen en forma anloga.
(De 2 orden o superior se llaman DERIVADAS DE ORDEN SUPERIOR).
Teorema:
- Si
f
es de clase
2
C ,entonces:
2 2
f f
x y y x
2.3 Derivadas de Orden Superior. Teorema de Taylor
29
Instituto de Matemtica
Universidad Austral de Chile
Teorema de Taylor:
- Recordemos que para una funcin
f
de una variable con derivadas hasta orden 1 k +
el Teorema de Taylor afirma que:
2
( ) ( )
( ) ( ) ( ) ...
2! !
k
k
o o
o o o k
f x f x
f x h f x f x h h h R
k
+ + + + + +
(
k
R
resto de ordenk )
Frmula de Taylor de 1er Orden:
:
n
f D
, Dabierto,
o
x D ,
f
de clase
1
C en .
o
x
Entonces:
1
1
( ) ( ) ( )
n
o o o
i
i
i
f
f x h f x x h R
x
+ + +
(
1
R
resto de 1er orden, 1
0
lim 0
h
R
h
)
2.3 Derivadas de Orden Superior. Teorema de Taylor
30
Instituto de Matemtica
Universidad Austral de Chile
O sea:
1 2
1 2
de en
Diferencial de en
( ) ( ) ( ) ( ) ... ( )
o
o
o o o o o
n
n
Incremento f x
f x
f f f
f x h f x x h x h x h
x x x
+ + + +
Esta frmula permite aproximar el valor del incremento que experimenta una funcin,
haciendo uso de sus derivadas parciales.
-La diferencial de
f
se anota:
Para n=2:
f f
df dx dy
x y
+
Para n=3:
f f f
df dx dy dz
x y z
+ +
2.3 Derivadas de Orden Superior. Teorema de Taylor
31
Instituto de Matemtica
Universidad Austral de Chile
Frmula de Taylor de 2do Orden:
:
n
f D
, Dabierto,
o
x D ,
f
de clase
2
C en .
o
x
Entonces:
Hessiano de en
2
2
1 , 1
Diferencial de en
1
( ) ( ) ( ) ( )
2
o
o
f x
n n
o o o o
i i j
i i j
i i j
f x
f f
f x h f x x h x hh R
x x x
+ + + +
(
2
R
resto de 2do orden, 2
2
0
lim 0
h
R
h
)
2.4 Extremos de Funciones de Varias Variables
32
Instituto de Matemtica
Universidad Austral de Chile
Extremos de Funciones de Varias Variables :
Extremos Relativos :
:
n
f D
, Dabierto,
o x D
o x Es punto mnimo relativo de
f
si:
( )/ ( ), o o V x x V x
( ) ( ) o f x f x
( ) o f x
Se llama valor mnimo relativo de
. f
o x Es punto mximo relativo de
f
si:
( )/ ( ), o o V x x V x
( ) ( ) o f x f x
( ) o f x
Se llama valor mximo relativo de
. f
o x
Es punto extremo relativo si es punto mnimo relativo o punto mximo relativo.
Observaciones:
-
( ) o V x
es vecindad del punto
o
x
- Tambin se les denomina extremos locales.
O sea:
(0) 0 g
Pero:
( ) ( ) o g t f x tv v +
As:
(0) ( ) 0 o g f x v
Como esta relacin se cumple:
2
, v
Entonces:
( ) 0 o f x
2.4 Extremos de Funciones de Varias Variables
33
Instituto de Matemtica
Universidad Austral de Chile
Teorema 1:
:
n
f D
, Dabierto,
f
diferenciable.
(
o
x D
, es punto extremo relativo de
f
)
( ( ) 0) o f x
Demostracin :(Para n=2)
Supongamos que
o x es punto mximo relativo. Sea vel vector no nulo cualquiera,
o x tv + es la recta que pasa por
o x
con direccin v,
( ) ( ) o g t f x tv +
es una funcin real
de una variable que tiene mximo relativo en 0 t .
2.4 Extremos de Funciones de Varias Variables
34
Instituto de Matemtica
Universidad Austral de Chile
Observaciones:
1) De acuerdo a este teorema tenemos:
o
x es punto extremo relativo de
f ( ) 0 o f x f
no es diferenciable.
2) Puntos Crticos de
f
son los puntos x D tales que:
( ) 0 f x f
no es
diferenciable en . x Estos son los candidatos a puntos extremos relativos.
3) Un punto crtico que no es punto extremo relativo se llama punto silla.
4) Para n=2 tenemos:
( , ) , x y D ( , ) x y
es punto crtico de
. f
Si
( , ) 0 ( , ) 0
f f
x y x y
x y
_
,
(
f
no es diferenciable en
( , ) x y
).
5) Para determinar si un punto critico es punto mnimo relativos, punto mximo relativo o
punto silla, se requiere de otro teorema, que se enunciar solo para n=2.
2.4 Extremos de Funciones de Varias Variables
35
Instituto de Matemtica
Universidad Austral de Chile
Teorema 2:
2
: f D
, Dabierto,
f
de clase
2
C :
( )
,
o o
x y
punto crtico de
f
.
Sea:
2 2
2
2
2 2 2
2 2
2 2
2
( , ) ( , )
( , ) ( , ) ( , )
( , ) ( , )
o o o o
o o o o o o
o o o o
f f
x y x y
x y x
f f f
x y x y x y
x y x y
f f
x y x y
x y y
_
,
Entonces:
1) 0 >
2
2
( , ) 0 ( , )
o o o o
f
x y x y
x
>
Es punto mnimo relativo de
f
.
2) 0 >
2
2
( , ) 0 ( , )
o o o o
f
x y x y
x
<
Es punto mximo relativo de
f
.
3) 0 < ( , )
o o
x y
Es punto silla de
f
.
4) 0: No hay informacin.
2.4 Extremos de Funciones de Varias Variables
36
Instituto de Matemtica
Universidad Austral de Chile
Observaciones
se llama DISCRIMINANTE de
f
en
( , )
o o
x y
, y es el determinante de la matriz Hessiana,
llamado tambin HESSIANO de
f
.
Extremos Condicionados. Multiplicadores de Lagrange:
Teorema 3:
:
n
f D
,
:
n
g D
,
, f g
1
C .
S conjunto de nivel cde
g
.
O sea:
{ }
/ ( ) S x D g x c
Sea
/ ( ) 0.
o o
x S g x
Si
o
x
es un punto extremo relativo de
f
restringido a S, entonces existe un nmero real , tal que:
( ) ( )
o o
f x g x
2.4 Extremos de Funciones de Varias Variables
37
Instituto de Matemtica
Universidad Austral de Chile
Observaciones:
1) Segn el teorema, para hallar puntos extremos relativos de una funcin
f
tales que
cumplen una condicin
( ) g x c
se debe hallar puntos xque cumplan la ecuacin:
( ) ( )
f x g x
El nmero se llama multiplicador de Lagrange.
2) Si se consideran ms de una condicin:
( ) ( ) ( )
1 1 2 2
, ,...,
k k
g x c g x c g x c
el
teorema se generaliza y la ecuacin a resolver ser:
( ) ( ) ( ) ( )
1 1 2 2
... .
k k
f x g x g x g x + + +
siendo
1
,...,
k
multiplicadores de Lagrange.
3) El teorema solo permite hallar puntos crticos de
f
restringidos a la condicin dada, pero no
d mtodo para determinar si son mnimo o mximo. Para ello se pueden usar consideraciones
geomtricas (grficos) o usar el siguiente teorema:
Si f es funcin continua definida en un conjunto compacto (cerrado y
acotado) entonces f tiene mnimo y mximo.
2.4 Extremos de Funciones de Varias Variables
38
Instituto de Matemtica
Universidad Austral de Chile
Extremos Absolutos ( Para n=2)
Sea
2
D conjunto compacto tal que
( ) Fr D
es una curva suave unin de curvas suaves
1 2 3
( ) Fr D C C C
1 2 3
, , V V V
son puntos donde
( ) Fr D
no es suave (Vrtices de D).
Sea
o x D
o x es punto mnimo absoluto de
. f
Si x D ,
( ) ( )
o f x f x
( )
o f x
es el valor mnimo absoluto de
. f
o x Es punto mximo absoluto de
. f
Si x D ,
( ) ( )
o f x f x
( )
o f x
Es el valor mximo absoluto de
. f
2.4 Extremos de Funciones de Varias Variables
39
Instituto de Matemtica
Universidad Austral de Chile
De acuerdo al Teorema antes enunciado si
f
es continua, entonces
f
tiene mnimo y mximo
(absolutos) en
f
. Para hallarlos se procede como sigue:
2) Se halla puntos crticos de
f
restringidos a
( ). Fr D
(En forma separada en cada curva).
3) Se halla puntos donde
( ) Fr D
no es suave. (o sea intersecciones de las curvas que forman
la frontera).
4) Se evala
f
en todos los puntos hallados y se compara para determinar puntos y valores
extremos absolutos.
1) Se halla puntos crticos de
f
en
( ). Int D
2.5 Teorema de la funcin Implcita. Teorema de la funcin Inversa
40
Instituto de Matemtica
Universidad Austral de Chile
Teorema de la Funcin Implcita y de la Funcin Inversa :
Teorema 1: (Caso particular del Teorema de la funcin Implcita)
Sea
1
:
n
F
+
, Fde clase
1
. C
(Denotemos los puntos de
1 n+
por:
( , ) x z
,con ,
n
x z
)
Si
( , )
o
o
x z
satisface:
( , ) 0 ( , ) 0
o o
o o
F
F x z x z
z
Entonces vecindad /
n
o U x U
vecindad
/
o
V z V
y una nica funcin:
: , ( ) g U V z g x
Que satisface:
( ) o
o
g x z
y
( , ( )) 0 F x g x
2.5 Teorema de la funcin Implcita. Teorema de la funcin Inversa
41
Instituto de Matemtica
Universidad Austral de Chile
Ms an:
Si , x U z V satisfacen:
( , ) 0 F x z
entonces
( ) z g x
Adems
g
es de clase
1
C y sus derivadas parciales son:
, 1,...,
i
i
F
g x
i n
F
x
z
2.5 Teorema de la funcin Implcita. Teorema de la funcin Inversa
42
Instituto de Matemtica
Universidad Austral de Chile
Observaciones:
1) Para 2 n , el teorema afirma que una ecuacin de la forma:
( , , ) 0 F x y z
define
una funcin:
( , ) z g x y
en la vecindad de un cierto punto
( , , )
o o o
x y z
Si:
( , , ) 0
o o o
F x y z
( , ) 0
o o
F
x y
z
Y en tal caso:
F
z
x
F
x
z
,
F
z y
F
y
z
2.5 Teorema de la funcin Implcita. Teorema de la funcin Inversa
43
Instituto de Matemtica
Universidad Austral de Chile
2) El Teorema de la Funcin Implcita en forma general dice que:
Si tenemos un sistema:
1 1 1
2 1 1
1 1
( ,..., , ,..., ) 0
( ,..., , ,..., ) 0
...
( ,..., , ,..., ) 0
n m
n m
m n m
F x x z z
F x x z z
F x x z z
1 2
, ,...,
m
F F F
de clase
1
. C
2.5 Teorema de la funcin Implcita. Teorema de la funcin Inversa
44
Instituto de Matemtica
Universidad Austral de Chile
Y en tal caso las derivadas parciales de estas funciones mplicitas son:
1
1
1
1
( ,..., )
( ,..., ,..., )
( ,..., )
( ,..., ,..., )
m
j m
i
j
m
i m
F F
z x z
z
x
F F
z z z
Y se quiere despejar
1
,...,
m
z z
como funciones de
1
,...,
n
x x
, esto se puede hacer en una
vecindad de un punto
( , )o o
x z
si:
( , )
o o
x z
Cumple el sistema.
1
1
Determinante de la matriz Jacobiana
Jacobiano
( ,..., )
( , ) 0
( ,..., )
m
o o
m
F F
x z
z z
2.5 Teorema de la funcin Implcita. Teorema de la funcin Inversa
45
Instituto de Matemtica
Universidad Austral de Chile
3) Casos Particulares:
n=2, m=1:
( , , ) 0 F x y z
( , , ) 0 G x y z
Se puede expresar
, y z
en funcin de x ( O sea:
( ) y f x
,
( ) z g x
) en una
vecindad de
( , , )
o o o
x y z
( , , ) 0 ( , , ) 0
o o o o o o
F x y z G x y z
( , , ) ( , , )
( , )
( , , ) 0
( , )
( , , ) ( , , )
o o o o o o
o o o
o o o o o o
F F
x y z x y z
y z
F G
x y z
G G y z
x y z x y z
y z
2.5 Teorema de la funcin Implcita. Teorema de la funcin Inversa
46
Instituto de Matemtica
Universidad Austral de Chile
y las derivadas de estas funciones implcitas son:
( , )
( , )
,
( , )
( , )
F G
x z dy
dx F G
y z
( , )
( , )
,
( , )
( , )
F G
y x dz
dx F G
y z
4) Una aplicacin del Teorema de la Funcin Implicita es el Teorema de la funcin Inversa.
2.5 Teorema de la funcin Implcita. Teorema de la funcin Inversa
47
Instituto de Matemtica
Universidad Austral de Chile
Teorema 2: (Teorema de la Funcin Inversa)
Sea : ,
n n
F U
( ); y F x
1
( ,..., )
n
F F F
1 2
, ,... :
n
n
F F F U
de clase
1
C
Si
,
o
o
x y
son solucin del sistema:
1 1 1
2 1 2
1
( ,..., )
( ,..., )
...
( ,..., )
n
n
n n n
F x x y
F x x y
F x x y
y
1
1
( ,..., )
( ) 0
( ,..., )
n
o
n
F F
x
x x
2.5 Teorema de la funcin Implcita. Teorema de la funcin Inversa
48
Instituto de Matemtica
Universidad Austral de Chile
Entonces el sistema se puede resolver de manera nica para
1
,...,
n
x x
o sea:
( ) x G y
para
( )
o
x U x
y
( )
o
y V y
(Ges inversa local de F)
Adems Ges de clase
1
C y las derivadas parciales de sus componentes son:
1
1
1
1
( ,..., )
( ,..., ,..., )
( ,..., )
( ,..., ,..., )
n
j n
i
n
j
i n
F F
x y x
x
F F
y
x x x
, donde
1
1 1 1
2
2 1 2
1
( ,..., )
( ,..., )
...
( ,..., )
n
n
n
n n n
F Fx x y
F F x x y
F F x x y
Potrebbero piacerti anche
- Derivadas Parciales, Plano Tangente y Recta NormalDocumento11 pagineDerivadas Parciales, Plano Tangente y Recta NormalMiguel Angel Saravia CuevaNessuna valutazione finora
- Derivadas Parciales 2012-4Documento35 pagineDerivadas Parciales 2012-4Luis Vilchez Cabrera70% (10)
- Fórmulario Cálculo Avanzado PEP2 2.0Documento6 pagineFórmulario Cálculo Avanzado PEP2 2.0Francisco Javier Valenzuela RiquelmeNessuna valutazione finora
- Extremos de Una Función de Varias Variables PDFDocumento14 pagineExtremos de Una Función de Varias Variables PDFMiguel Angel Saravia CuevaNessuna valutazione finora
- Variables Aleatorias Distribuidas en Forma ConjuntaDocumento32 pagineVariables Aleatorias Distribuidas en Forma ConjuntaJimyhms Melgarejo SeguraNessuna valutazione finora
- Trabajo Jacobiana Hessiana.Documento12 pagineTrabajo Jacobiana Hessiana.Clinton Yeferson100% (1)
- Solucionario PC 2 2021-IDocumento4 pagineSolucionario PC 2 2021-Ibleachcs23Nessuna valutazione finora
- AM III Cap1Documento34 pagineAM III Cap1Guillermo Reyes AguilarNessuna valutazione finora
- Unidad N 3 Campos EscalaresDocumento29 pagineUnidad N 3 Campos EscalaresJorge Luis Gonzalez ArroyoNessuna valutazione finora
- Examenes Resueltos 2do Parcial Calculo IIDocumento10 pagineExamenes Resueltos 2do Parcial Calculo IIjn_hcNessuna valutazione finora
- 735 - 16.996.517 - 2024-1 TSP1 - Jose BastardoDocumento12 pagine735 - 16.996.517 - 2024-1 TSP1 - Jose Bastardojose bastardoNessuna valutazione finora
- Linealidad de La DerivadaDocumento22 pagineLinealidad de La DerivadaEuarizaNessuna valutazione finora
- Ayudantia 5 MAT024Documento6 pagineAyudantia 5 MAT024Maca AlbornozNessuna valutazione finora
- CALCULOII LFM NOTAS1AlumnosDocumento14 pagineCALCULOII LFM NOTAS1Alumnosalanmeco456Nessuna valutazione finora
- Funciones Reales de Variable Real. CálculoDocumento59 pagineFunciones Reales de Variable Real. CálculoAmIn20122Nessuna valutazione finora
- Bma01 2021 2 PC4 SolDocumento3 pagineBma01 2021 2 PC4 SolEmilio TapiaNessuna valutazione finora
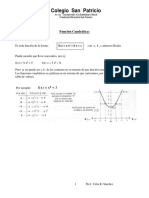
- Funcion CuadraticaDocumento14 pagineFuncion CuadraticaAlanNessuna valutazione finora
- DPEPDocumento9 pagineDPEPAnaMariaTantaleanRamirezNessuna valutazione finora
- Regla de La CadenaDocumento2 pagineRegla de La CadenaEduardo GonzalesNessuna valutazione finora
- M 63 Unidad 04Documento41 pagineM 63 Unidad 04Diego Turner CasablancasNessuna valutazione finora
- Calculo Diferencial en Varias VariablesDocumento48 pagineCalculo Diferencial en Varias VariablesAlberto Lagos100% (1)
- 178 179 1i 2007 2 Modelo de RespuestaDocumento8 pagine178 179 1i 2007 2 Modelo de RespuestaHernán VillarroelNessuna valutazione finora
- Pauta Prueba Parcial 3Documento3 paginePauta Prueba Parcial 3Esteban PantaNessuna valutazione finora
- Funciones de Varias VariableDocumento18 pagineFunciones de Varias VariableMaria RainNessuna valutazione finora
- Integrales Inmediatas. Integral Definida. Cálculo de ÁreasDocumento6 pagineIntegrales Inmediatas. Integral Definida. Cálculo de ÁreasAMYNNXXXX100% (1)
- Aplicaciones DerivadasDocumento8 pagineAplicaciones DerivadasLucas Cifuentes AbacaNessuna valutazione finora
- Calculo I - Límite - 2022Documento15 pagineCalculo I - Límite - 2022Guillermo maitaNessuna valutazione finora
- Taller 10Documento2 pagineTaller 10Luz CaicedoNessuna valutazione finora
- Teoria de Funciones CuadraticasDocumento30 pagineTeoria de Funciones CuadraticasSalvador CatalfamoNessuna valutazione finora
- Resumen de CVV para C3Documento18 pagineResumen de CVV para C3stbm22Nessuna valutazione finora
- TP7 DiferenciabilidadDocumento3 pagineTP7 DiferenciabilidadmarianelaNessuna valutazione finora
- 7 Aproximacion de FuncionesDocumento55 pagine7 Aproximacion de FuncionesWen Fox CordovaNessuna valutazione finora
- Tarea 2 - Literal .C. Jeison David GomezDocumento9 pagineTarea 2 - Literal .C. Jeison David GomezkristianNessuna valutazione finora
- 15 ExamenDocumento11 pagine15 Examenjudithcastrop6Nessuna valutazione finora
- Problemas Resueltos Aplicaciones Lineales 2013-14Documento8 pagineProblemas Resueltos Aplicaciones Lineales 2013-14miriNessuna valutazione finora
- Criterio de La Segunda DerivadaDocumento32 pagineCriterio de La Segunda Derivadahenry chaccaNessuna valutazione finora
- Pauta Ayudantía N°5Documento4 paginePauta Ayudantía N°5Juan David CruzNessuna valutazione finora
- UBA XXI Apunte Polinomio de Taylor PDFDocumento13 pagineUBA XXI Apunte Polinomio de Taylor PDFNathaly PuyaNessuna valutazione finora
- Segundo Trimestre 12-13-2bach CCSSDocumento21 pagineSegundo Trimestre 12-13-2bach CCSSJulioEguizabaAlamañacNessuna valutazione finora
- Multiplicadores de LagrangeDocumento6 pagineMultiplicadores de LagrangeCesar Mamani100% (2)
- Taller Cal Int 2019Documento17 pagineTaller Cal Int 2019Maria Paula Caro DuarteNessuna valutazione finora
- Taller e Scald IfDocumento20 pagineTaller e Scald IfAlejandra Torres GómezNessuna valutazione finora
- Capitulo I (Derivadas)Documento17 pagineCapitulo I (Derivadas)JhorviPizarroQNessuna valutazione finora
- Regla Lopital 2011Documento8 pagineRegla Lopital 2011Cyntii GodoyNessuna valutazione finora
- TP4 Derivadas Parciales - Diferenciabilidad - Plano TangenteDocumento3 pagineTP4 Derivadas Parciales - Diferenciabilidad - Plano TangenteCinthia MolloNessuna valutazione finora
- Algebra PolinomiosDocumento11 pagineAlgebra Polinomioscarlos_ticsNessuna valutazione finora
- Notas C2 1Documento34 pagineNotas C2 1Isaac López LópezNessuna valutazione finora
- Método de LagrangeDocumento4 pagineMétodo de LagrangeMariana hernandezNessuna valutazione finora
- Ejercicios y PR Ctica 2ADocumento11 pagineEjercicios y PR Ctica 2APablo S.ReyeroNessuna valutazione finora
- Teoría de cuerpos y teoría de GaloisDa EverandTeoría de cuerpos y teoría de GaloisValutazione: 5 su 5 stelle5/5 (1)
- Geometric modeling in computer: Aided geometric designDa EverandGeometric modeling in computer: Aided geometric designNessuna valutazione finora
- La ecuación general de segundo grado en dos y tres variablesDa EverandLa ecuación general de segundo grado en dos y tres variablesNessuna valutazione finora
- Geometria - SegmentosDocumento3 pagineGeometria - Segmentosthecesar5xNessuna valutazione finora
- S01 S1-Sistema de UnidadesDocumento30 pagineS01 S1-Sistema de Unidadesthecesar5xNessuna valutazione finora
- S06 s1 Leyes de NewtonDocumento16 pagineS06 s1 Leyes de Newtonthecesar5xNessuna valutazione finora
- Tarea 1 AutocadDocumento3 pagineTarea 1 Autocadthecesar5xNessuna valutazione finora
- S.06.Si - Centro de GravedadDocumento2 pagineS.06.Si - Centro de Gravedadthecesar5xNessuna valutazione finora
- S01 s2-VECTORESDocumento19 pagineS01 s2-VECTORESthecesar5xNessuna valutazione finora
- Raz. Mate Problemas de ConjuntosDocumento4 pagineRaz. Mate Problemas de Conjuntosthecesar5xNessuna valutazione finora
- Trigonometria - Conversión de Sistemas TrigonométricosDocumento8 pagineTrigonometria - Conversión de Sistemas Trigonométricosthecesar5xNessuna valutazione finora
- Raz. Mate - Teoria de Conjuntos - Extension BIDocumento5 pagineRaz. Mate - Teoria de Conjuntos - Extension BIthecesar5xNessuna valutazione finora
- Geometria - Propiedades Del TrianguloDocumento5 pagineGeometria - Propiedades Del Triangulothecesar5x100% (1)
- Algebra - Monomios y PolinomiosDocumento5 pagineAlgebra - Monomios y Polinomiosthecesar5xNessuna valutazione finora
- Problemas de Ley de KirchhoffDocumento1 paginaProblemas de Ley de Kirchhoffthecesar5xNessuna valutazione finora
- Raz. Matematico - Operaciones SucesivasDocumento5 pagineRaz. Matematico - Operaciones Sucesivasthecesar5xNessuna valutazione finora
- Fisica Análisis-Vectorial-II - Vector Suma y Vector DiferenciaDocumento6 pagineFisica Análisis-Vectorial-II - Vector Suma y Vector Diferenciathecesar5xNessuna valutazione finora
- BiofisicaDocumento68 pagineBiofisicathecesar5xNessuna valutazione finora
- Biofisica - Grupo 5 - Radiaciones y Accidente NuclearesDocumento35 pagineBiofisica - Grupo 5 - Radiaciones y Accidente Nuclearesthecesar5xNessuna valutazione finora
- BiofisicaDocumento68 pagineBiofisicathecesar5xNessuna valutazione finora
- Biofisica - Grupo 6 - Ondas ElectromagnéticasDocumento45 pagineBiofisica - Grupo 6 - Ondas Electromagnéticasthecesar5xNessuna valutazione finora
- BiofisicaDocumento30 pagineBiofisicathecesar5xNessuna valutazione finora
- Biofisica - Grupo 3 - Radiologia y TomografiaDocumento73 pagineBiofisica - Grupo 3 - Radiologia y Tomografiathecesar5xNessuna valutazione finora
- BiofisicaDocumento30 pagineBiofisicathecesar5xNessuna valutazione finora
- 1 - Aritmetica 4to - IIIBDocumento10 pagine1 - Aritmetica 4to - IIIBthecesar5xNessuna valutazione finora
- Materiales de ColegioDocumento15 pagineMateriales de ColegioEduardo QuispeNessuna valutazione finora
- Biofisica - Grupo 4 - Sustancias RadioactivasDocumento65 pagineBiofisica - Grupo 4 - Sustancias Radioactivasthecesar5xNessuna valutazione finora
- Biofisica - Grupo 7 - Tratamiento Con ElectricidadDocumento15 pagineBiofisica - Grupo 7 - Tratamiento Con Electricidadthecesar5xNessuna valutazione finora
- Clonaci OnDocumento2 pagineClonaci Onthecesar5xNessuna valutazione finora
- DILATACIÓNDocumento3 pagineDILATACIÓNthecesar5xNessuna valutazione finora
- Autobuses 1Documento2 pagineAutobuses 1thecesar5xNessuna valutazione finora
- Tesis Completa Xavier Fuentes BayneDocumento132 pagineTesis Completa Xavier Fuentes BayneHans Mikel Zapata SilvaNessuna valutazione finora
- 05 - División Algebraica I (Horner y Ruffini)Documento4 pagine05 - División Algebraica I (Horner y Ruffini)thecesar5xNessuna valutazione finora