Documenti di Didattica
Documenti di Professioni
Documenti di Cultura
Fisika Teknik
Caricato da
Bagus BimantaraDescrizione originale:
Copyright
Formati disponibili
Condividi questo documento
Condividi o incorpora il documento
Hai trovato utile questo documento?
Questo contenuto è inappropriato?
Segnala questo documentoCopyright:
Formati disponibili
Fisika Teknik
Caricato da
Bagus BimantaraCopyright:
Formati disponibili
<+++< 2012
Fisika Teknik
Taharuddin
chxtahar@unila.ac.id
Jl. Sumantri Brojonegoro No.1 Gd. Meneng
Jurusan Teknik Kimia Fakultas Teknik
UNIVERSITAS LAMPUNG
2012
<+++< 2012
2/9/16
<+++< 2012
Introduction(1)
As a first step in studying classical mechanics,
we describe motion in terms of space and time
while ignoring the agents that caused that motion.
This portion of classical mechanics is called
kinematics. (The word kinematics has the same root
as cinema. Can you see why?) In this chapter we
consider only motion in one dimension. We first
define displacement, velocity, and acceleration.
Then, using these concepts, we study the motion of
objects traveling in one dimension with a constant
acceleration.
2/9/16
<+++< 2012
Introduction(2)
From everyday experience we recognize that
motion represents a continuous change in the
position of an object. In physics we are concerned
with three types of motion: translational, rotational,
and vibrational. A car moving down a highway is an
example of translational motion, the Earths spin on
its axis is an example of rotational motion, and the
back-and-forth movement of a pendulum is an
example of vibrational motion. In this and the next
few chapters, we are concerned only with
translational motion.
2/9/16
<+++< 2012
Introduction(3)
In our study of translational motion, we describe
the moving object as a particle regardless of its
size. In general, a particle is a point-like mass
having infinitesimal size. For example, if we wish to
describe the motion of the Earth around the Sun, we
can treat the Earth as a particle and obtain
reasonably accurate data about its orbit. This
approximation is justified because the radius of the
Earths orbit is large compared with the dimensions
of the Earth and the Sun.
2/9/16
<+++< 2012
DISPLACEMENT, VELOCITY, AND SPEED
The Meaning of Shape for a p-t Graph
Our study of 1-dimensional kinematics has been
concerned with the multiple means by which the
motion of objects can be represented. Such means
include the use of words, the use of diagrams, the
use of numbers, the use of equations, and the use
of graphs. Lesson 3 focuses on the use of position
vs. time graphs to describe motion. As we will learn,
the specific features of the motion of objects are
demonstrated by the shape and the slope of the
lines on a position vs. time graph. The first part of
this lesson involves a study of the relationship
between the shape of a p-t graph and the motion of
the object.
2/9/16
6
<+++< 2012
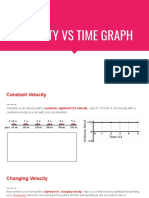
To begin, consider a car moving with a constant,
rightward (+) velocity - say of +10 m/s.
If the position-time data for
such a car were graphed, then
the resulting graph would look
like the graph at the right.
Note that a motion described
as a constant, positive velocity
results in a line of constant
and positive slope when
plotted as a position-time
graph.
2/9/16
<+++< 2012
Now consider a car moving with a rightward (+),
changing velocity - that is, a car that is moving
rightward but speeding up or accelerating.
The position vs. time
graphs for the two types of
motion - constant velocity
and changing velocity (
acceleration) - are depicted
as follows.
2/9/16
<+++< 2012
Resume
2/9/16
<+++< 2012
The Importance of Slope
The shapes of the position versus time graphs for these two
basic types of motion - constant velocity motion and
accelerated motion (i.e., changing velocity) - reveal an
important principle. The principle is that the slope of the line
on a position-time graph reveals useful information about
the velocity of the object. It is often said, "As the slope goes,
so goes the velocity." Whatever characteristics the velocity
has, the slope will exhibit the same (and vice versa). If the
velocity is constant, then the slope is constant (i.e., a
straight line). If the velocity is changing, then the slope is
changing (i.e., a curved line). If the velocity is positive, then
the slope is positive (i.e., moving upwards and to the right).
This very principle can be extended to any motion
conceivable.
2/9/16
10
<+++< 2012
Consider the graphs below as example applications of this principle
concerning the slope of the line on a position versus time graph. The
graph on the left is representative of an object that is moving with a
positive velocity (as denoted by the positive slope), a constant velocity
(as denoted by the constant slope) and a small velocity (as denoted by
the small slope). The graph on the right has similar features - there is a
constant, positive velocity (as denoted by the constant, positive slope).
However, the slope of the graph on the right is larger than that on the
left. This larger slope is indicative of a larger velocity. The object
represented by the graph on the right is traveling faster than the
object represented by the graph on the left. The principle of slope can
be used to extract relevant motion characteristics from a position vs.
time graph. As the slope goes, so goes the velocity.
2/9/16
11
<+++< 2012
Consider the graphs below as another application of this principle of
slope. The graph on the left is representative of an object that is
moving with a negative velocity (as denoted by the negative slope),
a constant velocity (as denoted by the constant slope) and a small
velocity (as denoted by the small slope). The graph on the right has
similar features - there is a constant, negative velocity (as denoted
by the constant, negative slope). However, the slope of the graph on
the right is larger than that on the left. Once more, this larger slope
is indicative of a larger velocity. The object represented by the graph
on the right is traveling faster than the object represented by the
graph on the left.
2/9/16
12
<+++< 2012
As a final application of this principle of slope, consider the two graphs below.
Both graphs show plotted points forming a curved line. Curved lines have
changing slope; they may start with a very small slope and begin curving
sharply (either upwards or downwards) towards a large slope. In either case,
the curved line of changing slope is a sign of accelerated motion (i.e.,
changing velocity). Applying the principle of slope to the graph on the left, one
would conclude that the object depicted by the graph is moving with a
negative velocity (since the slope is negative ). Furthermore, the object is
starting with a small velocity (the slope starts out with a small slope) and
finishes with a large velocity (the slope becomes large). That would mean that
this object is moving in the negative direction and speeding up (the small
velocity turns into a larger velocity). This is an example of
negative acceleration - moving in the negative direction and speeding up. The
graph on the right also depicts an object with negative velocity (since there is
a negative slope). The object begins with a high velocity (the slope is initially
large) and finishes with a small velocity (since the slope becomes smaller). So
this object is moving in the negative direction and slowing down. This is an
example of positive acceleration.
2/9/16
13
<+++< 2012
Now consider a car moving at a constant velocity of +5
m/s for 5 seconds, abruptly stopping, and then remaining
at rest (v = 0 m/s) for 5 seconds.
If the position-time data for such a
car were graphed, then the resulting
graph would look like the graph at
the right. For the first five seconds
the line on the graph slopes up 5
meters for every 1 second along the
horizontal (time) axis. That is, the line
on the position vs. time graph has a
slope of +5 meters/1 second for the
first five seconds. Thus, the slope of
the line on the graph equals the
velocity of the car. During the last 5
seconds (5 to 10 seconds), the line
2/9/16
14
<+++< 2012
Observe the two cars below. The blue car starts ahead of"
the red car. (The red car actually starts off the screen.) Since
the red car is moving faster, it eventually catches up with
and passes the blue car. Observe the position-time graphs
for these two cars. The position-time plot of each car's
motion is depicted by a diagonal line with a constant slope.
This diagonal line is an indicator of a constant velocity. At the
time that the cars are side by side, the lines intersect. That
is, the two cars share the same position at that instant in
time. The lines would not intersect for a
velocity vs. time graph; there is never an instant in time in
which they share the same velocity. The two cars have the
same position at seven seconds; yet they never have the
same velocity at any instant in time
2/9/16
15
<+++< 2012
Let's begin by considering the position versus time graph
below.
The line is sloping upwards to the right. But mathematically, by how
much does it slope upwards for every 1 second along the horizontal
(time) axis? To answer this question we must use the slope equation.
The slope equation says that the slope of a line is found by
determining the amount of rise of the line between any two points
divided by the amount of run of the line between the same two
points.
2/9/16
16
<+++< 2012
In other words:
Pick two points on the line and determine their
coordinates.
Determine the difference in y-coordinates of these two
points (rise).
Determine the difference in x-coordinates for these two
points (run).
Divide the difference in y-coordinates by the difference
in x-coordinates (rise/run or slope).
The diagram below shows this method being applied to
determine the slope of the line. Note that three different
calculations are performed for three different sets of two
points on the line. In each case, the result is the same: the
slope is 10 m/s.
2/9/16
17
<+++< 2012
So that was easy - rise over run is all that is involved.
Now let's attempt a more difficult example. Consider the
graph below. Note that the slope is not positive but
rather negative; that is, the line slopes in the downward
direction. Note also that the line on the graph does not
pass through the origin. Slope calculations are relatively
easy when the line passes through the origin since one
of the points is (0,0). But that is not the case here. Test
your understanding of slope calculations by determining
the slope of the line below. Then click the button to
check your answer.
2/9/16
18
<+++< 2012
2/9/16
19
<+++< 2012
Check Your Understanding
Determine the velocity (i.e., slope) of the object as
portrayed by the graph below. When you believe
you know the answer (and not before), click the
button to check it.
2/9/16
20
<+++< 2012
Consider a car moving with a constant, rightward (+)
velocity - say of +10 m/s. As learned in an earlier lesson,
a car moving with a constant velocity is a car with zero
acceleration.
If the velocity-time data for such a car were graphed, then the
resulting graph would look like the graph at the right. Note
that a motion described as a constant, positive velocity results
in a line of zero slope (a horizontal line has zero slope) when
plotted as a velocity-time graph. Furthermore, only positive
velocity values are plotted, corresponding to a motion with
positive velocity
2/9/16
21
<+++< 2012
Now consider a car moving with a rightward (+),
changing velocity - that is, a car that is moving rightward
but speeding up or accelerating. Since the car is moving
in the positive direction and speeding up, the car is said
to have a positive acceleration.
If the velocity-time data for such a car were graphed, then the
resulting graph would look like the graph at the right. Note
that a motion described as a changing, positive velocity
results in a sloped line when plotted as a velocity-time graph.
The slope of the line is positive, corresponding to the positive
acceleration. Furthermore, only positive velocity values are
plotted, corresponding to a motion with positive velocity.
2/9/16
22
<+++< 2012
The velocity vs. time graphs for the two types of motion constant velocity and changing velocity (acceleration) - can be
summarized as follows.
The shapes of the velocity vs. time graphs for these two basic types
of motion - constant velocity motion and accelerated motion (i.e.,
changing velocity) - reveal an important principle. The principle is
that the slope of the line on a velocity-time graph reveals useful
information about the acceleration of the object. If the acceleration
is zero, then the slope is zero (i.e., a horizontal line). If the
acceleration is positive, then the slope is positive (i.e., an upward
sloping line). If the acceleration is negative, then the slope is
negative (i.e., a downward sloping line). This very principle can be
extended to any conceivable motion.
2/9/16
23
<+++< 2012
The slope of a velocity-time graph reveals information about an
object's acceleration. But how can one tell whether the object is
moving in the positive direction (i.e., positive velocity) or in the
negative direction (i.e., negative velocity)? And how can one tell if the
object is speeding up or slowing down?
The answers to these questions hinge on one's ability to read a graph.
Since the graph is a velocity-time graph, the velocity would be
positive whenever the line lies in the positive region (above the xaxis) of the graph. Similarly, the velocity would be negative whenever
the line lies in the negative region (below the x-axis) of the graph. As
learned in Lesson 1, a positive velocity means the object is moving in
the positive direction; and a negative velocity means the object is
moving in the negative direction. So one knows an object is moving in
the positive direction if the line is located in the positive region of the
graph (whether it is sloping up or sloping down). And one knows that
an object is moving in the negative direction if the line is located in
the negative region of the graph (whether it is sloping up or sloping
down). And finally, if a line crosses over the x-axis from the positive
region to the negative region of the graph (or vice versa), then the
object has changed directions.
2/9/16
24
<+++< 2012
2/9/16
25
<+++< 2012
Now how can one tell if the object is speeding up or slowing
down? Speeding up means that the magnitude (or numerical
value) of the velocity is getting large. For instance, an object
with a velocity changing from +3 m/s to + 9 m/s is speeding
up. Similarly, an object with a velocity changing from -3 m/s to
-9 m/s is also speeding up. In each case, the magnitude of the
velocity (the number itself, not the sign or direction) is
increasing; the speed is getting bigger. Given this fact, one
would believe that an object is speeding up if the line on a
velocity-time graph is changing from near the 0-velocity point
to a location further away from the 0-velocity point. That is, if
the line is getting further away from the x-axis (the 0-velocity
point), then the object is speeding up. And conversely, if the
line is approaching the x-axis, then the object is slowing down.
2/9/16
26
<+++< 2012
Acceleration
Observe the animation of the three cars below. Use the
animation to answer the three questions. (If necessary, review
the definition of acceleration.)
1.Which car or cars (red, green, and/or blue) are undergoing
an acceleration? Study each car individually in order to
determine the answer.
2.Which car (red, green, or blue) experiences the greatest
acceleration?
3.Consider the position-time graph at the right. Each one of
the three lines on the position-time graph corresponds to the
motion of one of the three cars. Match the appropriate line to
the particular color of car.
2/9/16
27
<+++< 2012
2/9/16
28
<+++< 2012
Constant Positive Velocity
Observe that the object below moves with a constant
velocity in the positive direction. The dot diagram shows
that each consecutive dot is the same distance apart
(i.e., a constant velocity). The position-time graph shows
that the slope is both constant (meaning a constant
velocity) and positive (meaning a positive velocity). The
velocity-time graph shows a horizontal line with zero
slope (meaning that there is zero acceleration); the line
is located in the positive region of the graph
(corresponding to a positive velocity). The accelerationtime graph shows a horizontal line at the zero mark
(meaning zero acceleration).
2/9/16
29
<+++< 2012
Constant Negative Velocity
Observe that the object below moves with a constant velocity
in the negative direction. The dot diagram shows that each
consecutive dot is the same distance apart (i.e., a constant
velocity). The position-time graph shows that the slope is both
constant (meaning a constant velocity) and negative (meaning
a negative velocity). The velocity-time graph shows a
horizontal line with zero slope (meaning that there is zero
acceleration); the line is located in the negative region of the
graph (corresponding to a negative velocity). The
acceleration-time graph shows a horizontal line at the zero
mark (meaning zero acceleration).
2/9/16
30
<+++< 2012
Positive Velocity and Positive Acceleration
Observe that the object below moves in the positive direction with
a changing velocity. An object which moves in the positive
direction has a positive velocity. If the object is speeding up, then
its acceleration vector is directed in the same direction as its
motion (in this case, a positive acceleration). The dot diagram
shows that each consecutive dot is not the same distance apart
(i.e., a changing velocity). The position-time graph shows that the
slope is changing (meaning a changing velocity) and positive
(meaning a positive velocity). The velocity-time graph shows a
line with a positive (upward) slope (meaning that there is a
positive acceleration); the line is located in the positive region of
the graph (corresponding to a positive velocity). The accelerationtime graph shows a horizontal line in the positive region of the
graph (meaning a positive acceleration).
2/9/16
31
<+++< 2012
Positive Velocity and Negative Acceleration
Observe that the object below moves in the positive direction
with a changing velocity. An object which moves in the
positive direction has a positive velocity. If the object is
slowing down then its acceleration vector is directed in the
opposite direction as its motion (in this case, a negative
acceleration). The dot diagram shows that each consecutive
dot is not the same distance apart (i.e., a changing velocity).
The position-time graph shows that the slope is changing
(meaning a changing velocity) and positive (meaning a
positive velocity). The velocity-time graph shows a line with a
negative (downward) slope (meaning that there is a negative
acceleration); the line is located in the positive region of the
graph (corresponding to a positive velocity). The accelerationtime graph shows a horizontal line in the negative region of
the graph (meaning a negative acceleration).
2/9/16
32
<+++< 2012
The Passing Lane
Observe the two cars below. The blue car starts ahead of" the
red car. (The red car actually starts off the screen.) Since the
red car is moving faster, it eventually catches up with and
passes the blue car. Observe the position-time graphs for
these two cars. The position-time plot of each car's motion is
depicted by a diagonal line with a constant slope. This
diagonal line is an indicator of a constant velocity. At the time
that the cars are side by side, the lines intersect. That is, the
two cars share the same position at that instant in time. The
lines would not intersect for a velocity vs. time graph; there is
never an instant in time in which they share the same velocity.
The two cars have the same position at seven seconds; yet
they never have the same velocity at any instant in time.
2/9/16
33
<+++< 2012
The Passing Lane
Observe the two cars below. The blue car starts ahead of" the red
car. (The red car actually starts off the screen.) Since the red car
is moving faster, it eventually catches up with and passes the
blue car. Observe the velocity-time graphs for these two cars.
Each car's motion is represented by a horizontal line, indicating a
constant velocity. Observe that even though the cars pass each
other, the lines on the velocity-time graphs do not intersect.
Since the cars never have the same velocity, the lines on the
velocity-time graph never cross. The lines would intersect for a
position vs. time graph; the fact that the red car passes the blue
car means that there is an instant in which they occupy the same
position. The two cars have the same position at seven seconds;
yet they never have the same velocity at any instant in time.
2/9/16
34
<+++< 2012
The Stoplight
A blue car moving at a constant speed of 10 m/s passes a red car that is at rest. This
occurs at a stoplight the moment that the light turns green. The clock is reset to 0
seconds and the velocity-time data for both cars are collected and plotted. The red car
accelerates from rest at 4 m/s/s for three seconds and then maintains a constant speed.
The blue car maintains a constant speed of 10 m/s for the entire 12 seconds. Observe
the motion and make meaning of the accompanying graphs to answer the following
questions:
1. What is the final velocity of a car that accelerates from rest at 4 m/s/s for three
seconds?
2. What is the displacement of each individual car after three seconds? (Consider a
kinematic equation or the area of the velocity-time graph.)
3. What is the slope of the line for the red car for the first three seconds?
4. What is the displacement of each individual car after nine seconds (use the area of
the velocity-time graph)?
5. Does the red car pass the blue car at three seconds? If not, then when does the red
car pass the blue car?
6. When lines on a velocity-time graph intersect, does it mean that the two cars are
passing by each other? If not, what does it mean?
2/9/16
35
<+++< 2012
1. Answers to the questions:
2. 12 m/s
3. Red Car: Area of Triangle = 0.5*b*h = 0.5*(3 s)*(12 m/s) =
18 m
Blue Car: Area of Rectangle = b*h = (3 s)*(10 m/s) = 30 m
4. slope = rise/run = (12 m/s- 0 m/s) / (3 s) = 4 m/s/s
5. Red Car: Area of Triangle + Area of Rectangle = 0.5*b1*h1
+ b2*h2 = 0.5*(3 s)*(12 m/s) +(9 s)*(12 m/s) = 18 m + 72
m = 90 m
Blue Car: Area of Rectangle = b*h = (9 s)*(10 m/s) = 90 m
6. No! The red car passes the blue car at 9 seconds. See
animation and the result of the above question.
7. No! When lines intersect on a velocity-time graph, it
means that the two cars have the same velocity. When
lines intersect on a position-time graph, it means that the
two cars are passing each other.
2/9/16
36
<+++< 2012
DISPLACEMENT, VELOCITY, AND SPEED
The motion of a particle is completely known if the
particles position in space is known at all times.
Consider a car moving back and forth along the x
axis, as shown in Figure 2.1a. When we begin
collecting position data, the car is 30 m to the right
of a road sign. (Let us assume that all data in this
example are known to two significant figures. To
convey this information, we should report the initial
position as 3.0 x 101 m. We have written this value
in this simpler form to make the discussion easier to
follow.) We start our clock and once every 10 s note
the cars location relative to the sign.
2/9/16
37
<+++< 2012
2/9/16
38
<+++< 2012
As you can see from Table 2.1, the car is
moving to the right (which we have defined
as the positive direction) during the first 10 s
of motion, from position A to position B. The
position values now begin to decrease,
however, because the car is backing up from
position B through position F. In fact, at D, 30
s after we start measuring, the car is
alongside the sign we are using as our origin
of coordinates. It continues moving to the left
and is more than 50 m to the left of the sign
when we stop recording information after our
sixth data point. A graph of this information
is presented in Figure 2.1b. Such a plot is
called a positiontime graph.
2/9/16
39
<+++< 2012
If a particle is moving, we can easily determine its
change in position. The displacement of a particle is
defined as its change in position. As it moves from
an initial position xi to a final position xf , its
displacement is given by xf - xi We use the Greek
letter delta () to denote the change in a quantity.
Therefore, we write the displacement, or change in
position, of the particle as:
From this definition we see that x is positive if xf is
greater than xi and negative if xf is less than xi .
2/9/16
40
<+++< 2012
A very easy mistake to make is not to recognize the difference
between displacement and distance traveled (Fig. 2.2). A baseball
player hitting a home run travels a distance of 360 ft in the trip
around the bases. However, the players displacement is zero
because his final and initial positions are identical.
Displacement is an example of a vector quantity. Many other
physical quantities, including velocity and acceleration, also are
vectors. In general, a vector is a physical quantity that requires
the specification of both direction and magnitude. By contrast, a
scalar is a quantity that has magnitude and no direction. In this
chapter, we use plus and minus signs to indicate vector direction.
We can do this because the chapter deals with one-dimensional
motion only; this means that any object we study can be moving
only along a straight line.
2/9/16
41
<+++< 2012
For example, for horizontal motion, let us arbitrarily
specify to the right as being the positive direction. It
follows that any object always moving to the right
undergoes a positive displacement + x, and any object
moving to the left undergoes a negative displacement -
x.
There is one very important point that has not yet been
mentioned. Note that the graph in Figure 2.1b does not
consist of just six data points but is actually a smooth
curve. The graph contains information about the entire
50-s interval during which we watched the car move. It is
much easier to see changes in position from the graph
than from a verbal description or even a table of numbers.
2/9/16
42
<+++< 2012
<+++<
2/9/16
43
Potrebbero piacerti anche
- The Meaning of Shape For A P-T GraphDocumento7 pagineThe Meaning of Shape For A P-T Graphcpverma2811Nessuna valutazione finora
- The Meaning of Shape For A P-T Graph: Position vs. Time GraphsDocumento20 pagineThe Meaning of Shape For A P-T Graph: Position vs. Time GraphsGilthonialzzNessuna valutazione finora
- M2L6 Velocity-Time GraphDocumento40 pagineM2L6 Velocity-Time GraphJoma Guerra ina moNessuna valutazione finora
- Calculate average speed from distance and timeDocumento7 pagineCalculate average speed from distance and timeShihabsirNessuna valutazione finora
- Summary - 02 PDFDocumento4 pagineSummary - 02 PDFImran MirzaNessuna valutazione finora
- 07 Accelerated MotionDocumento17 pagine07 Accelerated Motionapi-27085921Nessuna valutazione finora
- Unit2 Linear MotionDocumento22 pagineUnit2 Linear MotionAli Ahmad AliNessuna valutazione finora
- Velocity - Time GraphsDocumento31 pagineVelocity - Time GraphsCaloykOoy Danday DueñasNessuna valutazione finora
- Understanding Projectile Motion in Two DimensionsDocumento5 pagineUnderstanding Projectile Motion in Two DimensionsCyrus TrayagNessuna valutazione finora
- Motion Graphs: Understanding Speed and Acceleration from GraphsDocumento64 pagineMotion Graphs: Understanding Speed and Acceleration from GraphsKingsley ChengNessuna valutazione finora
- Physics VectorsDocumento24 paginePhysics VectorsNirvaniNessuna valutazione finora
- Acceleration WorksheetDocumento19 pagineAcceleration WorksheetdebbyhooiNessuna valutazione finora
- Using GraphsDocumento9 pagineUsing GraphswolfretonmathsNessuna valutazione finora
- CBSE Class 9 Science Chapter 8 Motion Revision NotesDocumento24 pagineCBSE Class 9 Science Chapter 8 Motion Revision NotesBriti DubeyNessuna valutazione finora
- Understanding motion graphsDocumento46 pagineUnderstanding motion graphsreanizaNessuna valutazione finora
- Uniformly Accelerated MotionDocumento7 pagineUniformly Accelerated MotionKtine TaoataoNessuna valutazione finora
- مذكرة شرح Physics - فيزياء لغات للصف الاول الثانوى لمدارس اللغات-الامتحان التعليمىDocumento20 pagineمذكرة شرح Physics - فيزياء لغات للصف الاول الثانوى لمدارس اللغات-الامتحان التعليمىRania Gamal Fouad100% (1)
- The Meaning of Shape For A P-T GraphDocumento4 pagineThe Meaning of Shape For A P-T GraphShon HanNessuna valutazione finora
- Understanding Constant AccelerationDocumento6 pagineUnderstanding Constant AccelerationSheila Padaoan GarciaNessuna valutazione finora
- ChapterDocumento14 pagineChapterjulietNessuna valutazione finora
- Motion Notes 1Documento6 pagineMotion Notes 1Amaan moyalNessuna valutazione finora
- Discussion of Theories (Experiment 3)Documento5 pagineDiscussion of Theories (Experiment 3)MarizNessuna valutazione finora
- Motion and Its FormulaesDocumento21 pagineMotion and Its Formulaessachin_itachiNessuna valutazione finora
- Motion and Its Description: Motion. in These Examples, Motion Is Easily Visible To Us. But in Some Cases, Motion Is NotDocumento18 pagineMotion and Its Description: Motion. in These Examples, Motion Is Easily Visible To Us. But in Some Cases, Motion Is NotrashidNessuna valutazione finora
- Mechanics Equations and FormulasDocumento12 pagineMechanics Equations and FormulasLiang LuNessuna valutazione finora
- Activity Sheet Week 3-4 3rd QTRDocumento7 pagineActivity Sheet Week 3-4 3rd QTRMarian Anion-GauranoNessuna valutazione finora
- Chapter 8 Motion: Key Concepts and Equations of MotionDocumento8 pagineChapter 8 Motion: Key Concepts and Equations of MotionmohamedNessuna valutazione finora
- Basics of KinematicsDocumento7 pagineBasics of KinematicsMarianne Kristelle FactorNessuna valutazione finora
- General Physics 1 - Motion GraphsDocumento6 pagineGeneral Physics 1 - Motion GraphsCarmina Jane DomantayNessuna valutazione finora
- Edexcel IAL Physics AS-level: Topic 1.3: MechanicsDocumento13 pagineEdexcel IAL Physics AS-level: Topic 1.3: MechanicsDiya FathimaNessuna valutazione finora
- Motion Along A Straight LineDocumento23 pagineMotion Along A Straight LineMina SamNessuna valutazione finora
- Vectors and scalars explainedDocumento83 pagineVectors and scalars explainedBirukNessuna valutazione finora
- PhysicsDocumento299 paginePhysicsAansa AsifNessuna valutazione finora
- KINEMATICS IN ONE DIRECTION: VECTORS REVIEWDocumento12 pagineKINEMATICS IN ONE DIRECTION: VECTORS REVIEWEdgar UbaldeNessuna valutazione finora
- Using A Graph To Get The General Equation For DisplacementDocumento11 pagineUsing A Graph To Get The General Equation For DisplacementAndrea KusickiNessuna valutazione finora
- Graphical Analysis and Vectors: Motion in 2D DimensionsDocumento10 pagineGraphical Analysis and Vectors: Motion in 2D DimensionsThaddeus LewisNessuna valutazione finora
- Motion Diagram1Documento16 pagineMotion Diagram1Shera100% (1)
- Constant Velocity and Acceleration Model SummaryDocumento10 pagineConstant Velocity and Acceleration Model Summaryapi-275962124Nessuna valutazione finora
- 2020 06 18 IX Physics 0Documento18 pagine2020 06 18 IX Physics 0ahanafdoNessuna valutazione finora
- Frames of reference in physics and their usesDocumento6 pagineFrames of reference in physics and their usesPrateek SharmaNessuna valutazione finora
- Distance Vs Time GraphsDocumento4 pagineDistance Vs Time GraphsMercedes DolendoNessuna valutazione finora
- Kinematics in One DimensionDocumento6 pagineKinematics in One DimensionSalahAL-HakimiNessuna valutazione finora
- Edexcel IAL Physics A-Level: Topic 1.3: MechanicsDocumento13 pagineEdexcel IAL Physics A-Level: Topic 1.3: MechanicsIshtiaque AhmedNessuna valutazione finora
- Variable Speed Car LabDocumento1 paginaVariable Speed Car Labapi-276694326Nessuna valutazione finora
- Speed and Motion ExplainedDocumento4 pagineSpeed and Motion Explainedismun nadhifah100% (1)
- Kinematics Equations, Graphs, and Assumptions QuizDocumento2 pagineKinematics Equations, Graphs, and Assumptions QuizDennisNessuna valutazione finora
- Summary - 01 PDFDocumento3 pagineSummary - 01 PDFImran MirzaNessuna valutazione finora
- PHYSICS 1 For StudentsDocumento21 paginePHYSICS 1 For StudentsWamm MadlaNessuna valutazione finora
- Gerak Lurus en-USDocumento9 pagineGerak Lurus en-USAri ChristianNessuna valutazione finora
- Motion - Speed Velocity and AccelerationDocumento51 pagineMotion - Speed Velocity and AccelerationJoric MagusaraNessuna valutazione finora
- A-level Physics Revision: Cheeky Revision ShortcutsDa EverandA-level Physics Revision: Cheeky Revision ShortcutsValutazione: 3 su 5 stelle3/5 (10)
- HW01 SIM KeyDocumento11 pagineHW01 SIM KeyRina MaiNessuna valutazione finora
- Kinema TicsDocumento5 pagineKinema TicsSamuel Muabia PlānetNessuna valutazione finora
- Lecture Notes On Straight-Line Motion and GraphsDocumento7 pagineLecture Notes On Straight-Line Motion and Graphscsharp testNessuna valutazione finora
- PC1431 Assignment 0 AnswersDocumento32 paginePC1431 Assignment 0 AnswersMikael Lee80% (5)
- SPEED & MOTION: UNDERSTANDING MOTION THROUGH GRAPHSDocumento6 pagineSPEED & MOTION: UNDERSTANDING MOTION THROUGH GRAPHSHien DuongNessuna valutazione finora
- Acceleration Due To GravityDocumento9 pagineAcceleration Due To GravityLheana MariNessuna valutazione finora
- Teacher's Notes: Gradients On GraphsDocumento52 pagineTeacher's Notes: Gradients On GraphsItz TeyyNessuna valutazione finora
- A Complete Course in Physics (Graphs) - First EditionDa EverandA Complete Course in Physics (Graphs) - First EditionNessuna valutazione finora
- A Level Physics 13 June2015Documento20 pagineA Level Physics 13 June2015Anthony0% (1)
- OCR Maths M2 Topic Questions From Papers Energy, Work and Power AnswersDocumento9 pagineOCR Maths M2 Topic Questions From Papers Energy, Work and Power Answersjunk filesNessuna valutazione finora
- Exjobb2003 Magnetisering Av GeneratorerDocumento38 pagineExjobb2003 Magnetisering Av GeneratorerhhxmanNessuna valutazione finora
- Composite Box Section PropertiesDocumento2 pagineComposite Box Section PropertiesCIVILNessuna valutazione finora
- FR3 CalculationsDocumento5 pagineFR3 CalculationsJoeco Abay-abayNessuna valutazione finora
- Electricity MarketDocumento27 pagineElectricity MarketcakesandfinancesNessuna valutazione finora
- Conservation of Energy: Physics 20 Unit C: Energy and WorkDocumento10 pagineConservation of Energy: Physics 20 Unit C: Energy and WorkUnzal FatehullahNessuna valutazione finora
- Sharp 21s Fx10v Ga 7s Ixc324wjDocumento9 pagineSharp 21s Fx10v Ga 7s Ixc324wjVăn Út Điện TửNessuna valutazione finora
- Energy Meters: Electronic Energy Meter Trivector Meter - ER300PDocumento12 pagineEnergy Meters: Electronic Energy Meter Trivector Meter - ER300PYashasvi VangalaNessuna valutazione finora
- Certificados Internacionais HPK 1 500Documento11 pagineCertificados Internacionais HPK 1 500JeanMacedoNessuna valutazione finora
- Wave and Oscillation QuestionsDocumento24 pagineWave and Oscillation QuestionsAlok ChaturvediNessuna valutazione finora
- Lecture Notes in Transportation Systems Engineering: Sight DistancesDocumento9 pagineLecture Notes in Transportation Systems Engineering: Sight DistancesAmit TahkurNessuna valutazione finora
- Double Cage Rotor Motor StructureDocumento2 pagineDouble Cage Rotor Motor Structuresalma100% (1)
- Hydro Electricity and Hydro Power Plant: By-Rajkumar Parihar (B11074)Documento34 pagineHydro Electricity and Hydro Power Plant: By-Rajkumar Parihar (B11074)AninVincelyNessuna valutazione finora
- Lecture # 05Documento14 pagineLecture # 05Rahil BalochNessuna valutazione finora
- A Presentation On 'Maxwell's Demon'Documento27 pagineA Presentation On 'Maxwell's Demon'luciferlightNessuna valutazione finora
- Engine MountDocumento8 pagineEngine MountAkash WaitageNessuna valutazione finora
- A Bidirectional LLC Resonant Converter With Automatic Forward and Backward Mode TransitiDocumento14 pagineA Bidirectional LLC Resonant Converter With Automatic Forward and Backward Mode TransitiMuhammad Saqib AliNessuna valutazione finora
- ViscosityDocumento4 pagineViscosityJan SetiawanNessuna valutazione finora
- Doepke-Specifying RCD Protection PDFDocumento3 pagineDoepke-Specifying RCD Protection PDFAN.ADAMMSNessuna valutazione finora
- Network Theorems LabDocumento7 pagineNetwork Theorems LabUmer FarooqNessuna valutazione finora
- 3PBO-M: Oil-Lubricated Rotary Vane Vacuum PumpDocumento2 pagine3PBO-M: Oil-Lubricated Rotary Vane Vacuum PumpAir-center CompresoresNessuna valutazione finora
- ASME SEC V Article 7 - 2001Documento15 pagineASME SEC V Article 7 - 2001Lhagva DalaibatNessuna valutazione finora
- Starting induction motors efficientlyDocumento25 pagineStarting induction motors efficientlyMonika VaitulionytėNessuna valutazione finora
- Virtual Laboratory: Circuit Construction Kit - DC: InstructionsDocumento6 pagineVirtual Laboratory: Circuit Construction Kit - DC: InstructionsSharon Gracia LigutanNessuna valutazione finora
- Unit Ii Multi-Stage Amplifiers: Types of CouplingDocumento58 pagineUnit Ii Multi-Stage Amplifiers: Types of Couplingcinthu chizhian22Nessuna valutazione finora
- Properties Therminol SPDocumento4 pagineProperties Therminol SPsanipoulouNessuna valutazione finora
- Commissioning Checklist 2Documento5 pagineCommissioning Checklist 2Gaurav TaydeNessuna valutazione finora
- 8 - Unit 4-PP Economics-Prob IDocumento10 pagine8 - Unit 4-PP Economics-Prob IMohammad Ibrahim KhaleelNessuna valutazione finora
- ELIVAC SMART VACUUM SYSTEM SAVES 80% ENERGYDocumento8 pagineELIVAC SMART VACUUM SYSTEM SAVES 80% ENERGYseimarfelipeNessuna valutazione finora