KINEMATICS OF PARTICLES

Kinematics of particles
Road Map
Rectilinear motion Curvilinear motion
x-y coord. n-t coord. r-u coord.
Engineering Dynamics
APPLICATIONS
The path of motion of each plane in
this formation can be tracked with
radar and their x, y, and z coordinates
(relative to a point on earth) recorded
as a function of time.
How can we determine the velocity
or acceleration of each plane at any
instant?

Engineering Dynamics
APPLICATIONS (continued)
A roller coaster car travels down
a fixed, helical path at a constant
speed.
How can we determine its
position or acceleration at any
instant?
Engineering Dynamics
General Curvilinear Motion
POSITION AND DISPLACEMENT
A particle moving along a curved path undergoes curvilinear motion.
Since the motion is often three-dimensional, vectors are used to
describe the motion.
A particle moves along a curve
defined by the path function, s.
The position of the particle at any instant is designated by the vector
r = r(t). Both the magnitude and direction of r may vary with time.
If the particle moves a distance As along the
curve during time interval At, the
displacement is determined by vector
subtraction: A r = r - r
Engineering Dynamics
General Curvilinear Motion
VELOCITY
Velocity represents the rate of change in the position of a
particle.
The average velocity of the particle
during the time increment At is
v
avg
= Ar/At .
The instantaneous velocity is the
time-derivative of position
v = dr/dt .
The velocity vector, v, is always
tangent to the path of motion.
The magnitude of v is called the
speed. As t0, the speed can be
obtained by differentiating the path
function (v = ds/dt). Note that this
is not a vector! Engineering Dynamics
General Curvilinear Motion
ACCELERATION
Acceleration represents the rate of change in the
velocity of a particle.
If a particles velocity changes from v to v over a
time increment At, the average acceleration during
that increment is:
a
avg
= Av/At = (v - v)/At
The instantaneous acceleration is the time-
derivative of velocity:
a = dv/dt = d
2
r/dt
2
Engineering Dynamics
Given: A particle travels along the curve from A to B in 2s. It takes 4s for it
to go from B to C and then 3s to go from C to D.
Find: Determine its average speed when it goes from A to D.
r
1
=10m, d=15m, r
2
=5m.
Solution:
56 . 38 ) 5 )( 2 (
4
1
15 ) 10 )( 2 (
4
1
= + + = t t
t
s
s m
t
s
v
t
t
sp
28 . 4
3 4 2
56 . 38
=
+ +
= =
Engineering Dynamics
Given: A car travelling along the straight portion of the road has the
velocities indicated in the figure when it arrives at a points A,B and
C. If it takes 3s to go from A to B and 5s from B to C.
Find: Determine the average acceleration between points A-B and A-C.
t
AB
=3s. t
BC
=5s. v
A
=20m/s, v
B
=30m/s v
C
=40m/s, =45 deg.
i v
A
20 =
j i v
B
21 . 21 21 . 21 + =
i v
C
40 =
3
20 21 . 21 21 . 21 i j i
t
v
a
AB
+
=
A
A
=
2
} 07 . 7 404 . 0 { s m j i a
AB
+ =
i
i i
t
v
a
AC
50 . 2
8
20 40
=

=
A
A
=
Solution:
Engineering Dynamics
KINEMATICS OF PARTICLES
Kinematics of particles
Road Map
Rectilinear motion Curvilinear motion
x-y coord. n-t coord. r-u coord.
Engineering Dynamics
Used to solve problems for
which the motion can be
convinently expressed in
terms of its x,y & z compts
Engineering Dynamics
When position vector
of particle P is given
by its rectangular
components
Engineering Dynamics
Representation of a
trajectory through
equations
Engineering Dynamics
Engineering Dynamics
Given: The flight path of the helicopter as it takes off from A is defined by
the parametric equations x=2t
2
and y=0.04t
3
, where t is the time in
seconds after takeoff.
Find: Determine the distance the helicopter is from point A and the
magnitude of its velocity and acceleration when t= 10s.
2
2t x =
3
04 . 0 t y =
At t =10s. x = 200m y =40m
. 204 ) 40 ( ) 200 (
2 2
m d = + =
Solution:
t
dt
dx
v
x
4 = =
4 = =
dt
dv
a
x
x
2
12 . 0 t
dt
dy
v
y
= =
t
dt
dv
a
y
y
24 . 0 = =
At t =10s.
s m v 8 . 41 ) 12 ( ) 40 (
2 2
= + =
2 2 2
66 . 4 ) 4 . 2 ( ) 4 ( s m a = + =
Engineering Dynamics
Engineering Dynamics
Engineering Dynamics
Engineering Dynamics
Engineering Dynamics
Projectile motion is a form of motion in which an object or
particle (called a projectile) is thrown obliquely near the
earth's surface, and it moves along a curved path under the
action of gravity.
Projectile motion only occurs when there is one force applied
at the beginning of the trajectory, after which there is no force
in operation apart from gravity
The path followed by a projectile is called its trajectory which
is directly influenced by gravity
Free flight motions are studied in terms of rectangular
component since projectiles acceleration always acts vertically
Motion of a Projectile
(Rectangular Components of Velocity & Acceleration)
A projectile is any object propelled through space by the exertion of a
force which ceases after launch
Motion of a Projectile
APPLICATIONS
(Rectangular Components of Velocity & Acceleration)
Motion of a Projectile
APPLICATIONS
(Rectangular Components of Velocity & Acceleration)
A kicker should know at what angle, u, and initial velocity, v
o,
he
must kick the ball to make a field goal.
For a given kick strength, at what angle should the ball be
kicked to get the maximum distance?
Engineering Dynamics
APPLICATIONS (continued)
A fireman wishes to know the maximum height on the wall he can
project water from the hose. At what angle, u, should he hold the
hose?
Engineering Dynamics
CONCEPT OF PROJECTILE MOTION
Projectile motion can be treated as two rectilinear motions, one in
the horizontal direction experiencing zero acceleration and the other
in the vertical direction experiencing constant acceleration (i.e.,
gravity).
For illustration, consider the two balls on the
left. The red ball falls from rest, whereas the
yellow ball is given a horizontal velocity. Each
picture in this sequence is taken after the same
time interval. Notice both balls are subjected to
the same downward acceleration since they
remain at the same elevation at any instant.
Also, note that the horizontal distance between
successive photos of the yellow ball is constant
since the velocity in the horizontal direction is
constant.
Engineering Dynamics
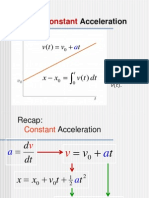
KINEMATIC EQUATIONS: HORIZONTAL MOTION
Since a
x
= 0, the velocity in the horizontal direction remains
constant (v
x
= v
ox
) and the position in the x direction can be
determined by:
x = x
o
+ (v
ox
)(t)
s = s
o
+ v
o
t + (1/2) a
c
t
2
v = v
o
+ a
c
t v
2
= (v
o
)
2
+ 2a
c
(s - s
o
)
Consider a projectile launched at (x
o
, y
o
)
Only force acting on the projectile is its weight, resulting in
constant downward acceleration
Air resistance is neglected
KINEMATIC EQUATIONS: VERTICAL MOTION
Since the positive y-axis is directed upward, a
y
= -g. Application of
the constant acceleration equations yields:
For any given problem, only two
of these three equations can be
used.
v
y
= v
oy
g(t)

y = y
o
+ (v
oy
)(t) g(t)
2

v
y
2
= v
oy
2
2g(y y
o
)
v = v
o
+ a
c
t s = s
o
+ v
o
t + (1/2) a
c
t
2
v
2
= (v
o
)
2
+ 2a
c
(s - s
o
)

Horizontal motion: Velocity in x direction is const v
x
=v
o
)
x

Verticle Motion,
Example 2
Solving the two equations together (two unknowns) yields
R = 19.0 m t
AB
= 2.48 s
Solution:
First, place the coordinate system at point A. Then write the
equation for horizontal motion.
+ x
B
= x
A
+ v
Ax
t
AB
and v
Ax
= 15 cos 40 m/s
Now write a vertical motion equation. Use the distance equation.
+ y
B
= y
A
+ v
Ay
t
AB
0.5g
c
t
AB
2
v
Ay
= 15 sin 40 m/s
Note that x
B
= R, x
A
= 0, y
B
= -(3/4)R, and y
A
= 0.
Given: Snowmobile is going 15
m/s at point A.
Find: The horizontal distance it
travels (R) and the time in
the air.
Engineering Dynamics
GROUP PROBLEM SOLVING
Given: Skier leaves the ramp at
u
A
= 25
o
and hits the
slope at B.
Find: The skiers initial speed v
A
.
Engineering Dynamics
GROUP PROBLEM SOLVING (continued)
Motion in x-direction:
Using x
B
= x
A
+ v
ox
(t
AB
)

=
t
AB
=
(4/5)100
v
A
(cos 25)
88.27
v
A
v
A
= 19.42 m/s
-64 = 0 + v
A
(sin 45)
88.27
v
A

(9.81)
88.27
v
A
2
Motion in y-direction:
Using y
B
= y
A
+ v
oy
(t
AB
) g(t
AB
)
2
Solution:
Engineering Dynamics
Example 1
Given: v
o
and
Find: The equation that defines
y as a function of x.
Solution: Using v
x
= v
o
cos
y = (v
o
sin )
x g x
v
o
cos 2 v
o
cos

2
( ) ( ) ( )
By substituting for t:
v
y
= v
o
sin and
We can write: x = (v
o
cos )t
and
y = (v
o
sin )t g(t)
2

Engineering Dynamics
Example 1 (continued):
The above equation is called the path equation which describes the
path of a particle in projectile motion.
Simplifying the last equation, we get:
y = (x tanu)
g x
2

2v
o
2
(1 + tan
2
u)
( )
Engineering Dynamics
Given: The fireman standing on the ladder directs the flow of water from his
hose to the fire at B.
Find: Determine the velocity of water at A if it is observed that the hose is
held at =20
o
.
Solution:
t v s s
o o
+ =
t v
o
A
) 20 cos ( 0 20 + =
A
v
t
28 . 21
=
2
2
1
t a t v s s
c o o
+ + =
) (
+
) ( | +
2
28 . 21
) 81 . 9 (
2
1 28 . 21
20 sin 0 10
|
|
.
|

\
|

|
|
.
|

\
|
=
A A
o
A
v v
v
1 . 2221 ) 20 (sin 28 . 21 10
2 2
=
A A
v v

s m v
A
57 . 28 =
10
20
Engineering Dynamics
Problem Sheet 3
Chapter 12
Problems 12-42 to 12-56