Chapter 5

Section 5.3
Medians and Altitudes
E
H
F
G
A B
C
M
A
B
C
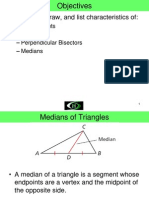
USING MEDIANS OF A TRIANGLE
A median of a triangle is a
segment whose endpoints are
a vertex of the triangle and the
midpoint of the opposite side.
D
USING MEDIANS OF A TRIANGLE
The three medians of a triangle are concurrent. The point
of concurrency is called the centroid of the triangle. The
centroid is always inside the triangle.
acute triangle right triangle obtuse triangle
centroid centroid centroid
The medians of a triangle have a special concurrency property.
THEOREM
THEOREM 5.7 Concurrency of Medians of a Triangle
USING MEDIANS OF A TRIANGLE
The medians of a triangle intersect at a point that is two-thirds
of the distance from each vertex to the midpoint of the
opposite side.
If P is the centroid of AABC, then
BP = BF
2
3
P
AP = AD
2
3
CP = CE
2
3
USING MEDIANS OF A TRIANGLE
The centroid of a triangle
can be used as its
balancing point.
A triangular model of uniform
thickness and density will
balance at the centroid of the triangle.
Using the Centroid of a Triangle
P is the centroid of AQRS shown below and PT = 5.
Find RT and RP.
SOLUTION
So, RP = 10 and RT = 15.
Then RP = RT = (15) = 10.
2
3
2
3
Because P is the centroid,
RP = RT.
2
3
Substituting 5 for PT, 5 = RT, so RT = 15.
1
3
Then PT = RT RP = RT
1
3
Finding the Centroid of a Triangle
Find the coordinates of the centroid of A JKL.
SOLUTION
The centroid is two thirds of the
distance from each vertex to the
midpoint of the opposite side.
(5, 8)
Choose the median KN. Find
the coordinates of N, the midpoint
of JL.
(7, 10)
(3, 6)
(5, 2)
3 + 7
2
,
6 + 10
2
=
10
2
,
16
2
= (5, 8)
The coordinates of N are
J
K
L
N
P
Find the coordinates of the centroid of A JKL.
SOLUTION
J
K
L
N
(5, 8)
(7, 10)
(3, 6)
(5, 2)
P
M
Find the distance from vertex K
to midpoint N. The distance from
K (5,2) to N(5,8) is 8 2, or 6 units.
[Yellow coordinates appear.]
Determine the coordinates of
the centroid, which is 6, or
4 units up from vertex K along
the median KN.
2
3
Finding the Centroid of a Triangle
The coordinates of the centroid P are (5, 2 + 4), or (5, 6)
(5, 6)
An altitude of a triangle is the perpendicular segment
from a vertex to the opposite side or to the line that contains
the opposite side. An altitude can lie inside, on, or outside
the triangle.
Every triangle has three altitudes. The lines containing the
altitudes are concurrent and intersect at a point called
the ortho center of the triangle.
USING ALTITUDES OF A TRIANGLE
Drawing Altitudes and Orthocenters
Where is the ortho center of an acute triangle?
SOLUTION
Draw an example.
The three altitudes intersect at G,
a point inside the triangle.
Drawing Altitudes and Orthocenters
The two legs, LM and KM,
are also altitudes. They intersect
at the triangles right angle.
This implies that the orthocenter is on the triangle
at M, the vertex of the right angle of the triangle.
Where is the orthocenter of a right triangle?
SOLUTION
Drawing Altitudes and Orthocenters
The three lines that contain the
altitudes intersect at W,
a point outside the triangle.
Where is the orthocenter of an obtuse triangle?
SOLUTION
THEOREM
USING ALTITUDES OF A TRIANGLE
THEOREM 5.8 Concurrency of Altitudes of a Triangle
The lines containing the altitudes of a triangle
are concurrent.
If AE, BF, and CD are the altitudes
of AABC, then the lines AE, BF, and
CD intersect at some point H.
Median
Angle Bisector
Perpendicular Bisector
Altitude
All Four
PO = 11
2
3
ML MP
| |
=
|
\ .
2
10
3
MP
| |
=
|
\ .
15 MP =
NQ NL LQ = +
2
3
NL NQ
| |
=
|
\ .
2
8
3
NQ
| |
=
|
\ .
12 NQ =
12 8 LQ = +
4 LQ =
HW #56
Pg 282-283 8-26 Even