Student: Sitan Chen Username: Math Geek ID#: 10636

USA Mathematical Talent Search

Year 22

Round 1

Problem 1

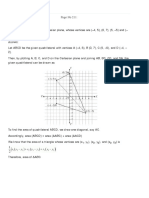
a). For convenience, label the bottom-left point with coordinates (0,0) and the top-right point with coordinates (8,2). Two vertically or horizontally adjacent points will dier in their y-coordinate or x-coordinate by 1, respectively. Note that each happy line that is not horizontal or vertical must pass through one point of the grid in each 1x9 row in the grid. If not, the happy line will pass through at most two rows and contain three points, and by the Pigeonhole Principle, two of these three points will lie in the same row, meaning the slope is 0, a contradiction. The slope of a non-horizontal, non-vertical line passing through a point in the bottom-most row and a point in the top-most row must have a rise of 2 and a run of a b where a = b and a, b [0, 8], meaning that a b can be any nonzero integer from -8 to 8, inclusive. However, note that if a b is odd, then the line will have an equation of the form, for some integers n and k, y0= 2 (x n). 2k + 1

Then for the middle row, where y = 1, we have that 2k+1 = x n x = 2k+1 + n. In this case, 2 2 the line will not pass through a lattice point in the middle row. On the other hand, an even value for a b will give a line with an equation of the form, for some integer k, y0= 2 (x n). 2k

Then for the middle row, where y = 1, we have that k = x n, in which case x is clearly an integer, meaning the line is happy. Thus, the slope of a non-vertical and non-horizontal happy line can only 1 be 4 , 1 , 1 , 1. 3 2 Now we split the problem into counting lines with certain slopes. First, there are 3 strictly horizontal lines and 9 strictly vertical lines. Next, for lines of slope -1, we start with the line that passes through (0,2) and (2,0) and count lines up to the one that passes through (6,2) and (8,0). There are 7 lines with slope -1. By symmetry, there are 7 lines with slope 1, from the line passing through (0,0) and (2,2) up to the line passing through (6,0) and (8,2). For lines of slope -1/2, we start with the line that passes through (0,2) and (4,0) and count lines up to the one that passes through (4,2) and (8,0). There are thus 5 lines with slope -1/2. By symmetry, we count 5 lines with slope 1/2.

Page 1 of Problem 1

Student: Sitan Chen Username: Math Geek ID#: 10636

USA Mathematical Talent Search

Year 22

Round 1

Problem 1

For lines of slope -1/3, we start with the line that passes through (0,2) and (6,0) and count lines up to the one that passes through (2,2) and (8,0). There are thus 3 lines with slope -1/3. By symmetry, we count 3 lines with slope 1/3. For lines of slope -1/4, we start with the line that passes through (0,2) and (8,0) and realize this is the only line with such a slope. Similarly, we realize there is only one line with slope 1/4. Thus, we have 3+9+7+7+5+5+3+3+1+1=3+9+2(1+3+5+7)= 44 .

b). We claim that the above set of 27 points has exactly 49 happy lines. We proceed with the same logic as the previous question. Label the bottom-left point (1,0) and the top-right point (9,2), with the same distance between adjacent points as in our solution to part a. Note again that any non-horizontal, non-vertical happy line must pass through a point of the set S in each row of the grid, or its slope by the Pigeonhole Principle is 0. A non-horizontal line passing through a point from the bottom row and a point in the top-row must must have a rise of 2 and a run of any value a b, where a [0, 9] and where b [1, 10]. By the same reasoning as in the previous question, a b must be even, so a b can be -10, -8, -6, -4, -2, 2, 4, 6, 8. Hence, a 1 1 non-horizontal, non-vertical happy line must have a slope of 5 , 1 , 3 , 1 , or 1. 4 2 First, there are 3 horizontal happy lines and 7 vertical happy lines. For lines of slope 1, we count starting from the line containing (1,0) and (3,2) up to the line containing (7,0) and (9,2). There are thus 7 lines of slope 1. For lines of slope -1, we count starting from the line containing (1,2) and (3,0) up to the line containing (7,2) and (9,0). There are 7 lines of slope -1. For lines of slope 1/2, we count starting from the line containing (1,0) and (5,2) up to the line containing (5,0) and (9,2). There are thus 5 lines of slope 1/2. For lines of slope -1/2, we count starting from the line containing (0,2) and (4,0) up to the line with (6,2) and (10,0), giving 7 lines of slope -1/2. For lines of slope 1/3, we count starting from the line containing (1,0) and (7,2) up to the line containing (3,0) and (9,2). There are thus 3 lines of slope 1/2. For lines of slope -1/3, we count starting from the line containing (0,2) and (6,0) up to the line with (4,2) and (10,0), giving 5 lines of slope -1/2. For lines of slope 1/4, we count starting from the line containing (1,0) and (9,2) and notice this is the only happy line of slope 1/4. There is thus 1 line of slope 1/4. For lines of slope -1/4, we count starting from the line containing (0,2) and (8,0) up to the line with (2,2) and (10,0), giving 3 lines of slope -1/2. Page 2 of Problem 1

Student: Sitan Chen Username: Math Geek ID#: 10636

USA Mathematical Talent Search

Year 22

Round 1

Problem 1

Finally, for lines of slope -1/5, we count starting from the line containing (0,2) and (10,0) and notice this is the only happy line of slope -1/5. there is thus 1 line of slope -1/5. Thus, having counted all happy lines, we nd there to be 1+1+3+3+5+5+7+7+7+3+7=49 happy lines, as desired.

Page 3 of Problem 1

Student: Sitan Chen Username: Math Geek ID#: 10636

USA Mathematical Talent Search

Year 22

Round 1

Problem 2

Note that we can track the movements of the beam by reecting the triangle through the side that the laser beam hits each time, as shown in the diagram. If the beam can return to A within a certain number of reections, then, obviously, we can draw a segment connecting A and its image under multiple reections so that the segment lies completely within the original triangle and all of its images under reection involved. Without loss of generality, say that the angle that AB and the beam make is less than 25 degrees, that is, the beam is rst red to the left of A. Indeed, this will give us the smallest angle between AB and the initial beam that makes the beam reach A . Clearly, the beam will rst hit BC, so we reect ABC, triangle One, through line BC to get A BC, triangle Two. It is Page 1 of Problem 2

Student: Sitan Chen Username: Math Geek ID#: 10636

USA Mathematical Talent Search

Year 22

Round 1

Problem 2

not hard to see that the next side the beam hits can only be BA , so we reect Two through BA to get A BC , triangle Three. Because ABC = 65 + 65 + 65 = 195 > 180, the only side that the beam can next hit is A C , so reect triangle Three through this line to get A B C , triangle Four. Notice that ABB = ABC + A BC + A BB = 130 + A BB . Triangle A BB is isosceles, and BA B = 50 + 50 = 100, so A BB = 40. Thus, AB B = 170 < 180, so the beam can now hit either C B or A B . We reect triangle Four through both to get triangles Five1 and Five2, respectively. Note in this case that the reex angle ABA is equal to the sum of reex angle ABC and the acute angle A BC , so, and reex ABC is already greater than 180 degrees, so so the beam will never hit A C. We know ABB < 180, so the beam can hit side A B , so we reect triangle Five1 through that line to get triangle Six1. Similarly, we know that because ABB < 180, the beam can hit side B C of triangle Five2, but because AA C = AA B + BA C + C A B + B A C = 25 + 50 + 50 + 50 = 175 < 180, the beam can also hit side A C . We reect through these two sides to get triangles Six2 and Six3, respectively. Note that among triangles labeled Five or below, besides A , no images of A exist other than A and A . A can only be reached if we initially re the beam at the midpoint of BC, while A cannot be reached because ABA > 180). However, notice in triangle Six2 the point A . Because ABA = ABB B BA < 180, the beam can reach A . In the triangles Six1 and Six2, no such image of A exists. To get to A , the beam needed 5 reections. Thus, the minimum number of reections is 5 reections . Finally, to nd the angle BAA , notice that, collectively, the image of the triangles One, Two, and Three reected about the line A C is the collection of triangles Four, Five2, and Six2. Thus, if we call the intersection of AA and BC the point D and the intersection of AA and B C the point D , then the two are actually images under reection through A C , as are B D and BD. We can conclude that BAD = B A D . We know that A B B = 65 + 65 + 40 = 170 and that ABB = 170. Thus, BAD + B A D + A B B + ABB = 360 2BAD = 360 170 170 = 20. Therefore, BAD = 10 degrees .

Page 2 of Problem 2

Student: Sitan Chen Username: Math Geek ID#: 10636

USA Mathematical Talent Search

Year 22

Round 1

Problem 3

We rst establish some values. Note that r2 + s2 + t2 = (r + s + t)2 2(rs + rt + st), so by Vietas formulas, the sum of the squares of the roots of f (x) is 42 2(6) = 4. Next, note that r2 s2 + r2 t2 + s2 t2 = (rs + rt + st)2 2rst(r + s + t), so by Vietas formulas, it is equal to 62 2(c)(4) = 36 + 8c. Finally, note that r2 s2 t2 = (rst)2 , which by Vietas formulas is equal to (c)2 = c2 . Now, change the left-hand side of the given relation between the roots to 1 1 1 + + . 2 2 4r 4s 4 t2 Because the given relation has r2 + s2 and similar terms in the denominator, we know they are not equal to zero, so we can multiply both sides by (4 r2 )(4 s2 )(4 t2 ) to get (4 r2 )(4 s2 )(4 t2 ) = (4 r2 )(4 s2 ) + (4 r2 )(4 t2 ) + (4 s2 )(4 t2 ). Expand to get 64 16(r2 + s2 + t2 ) + 4(r2 s2 + r2 t2 + s2 t2 ) r2 s2 t2 = 3(16) 8(r2 + s2 + t2 ) + r2 s2 + r2 t2 + s2 t2 . Substitute our known values in to get 64 16(4) + 4(36 + 8c) c2 = 48 8(4) + (36 + 8c). Combining like terms and rearranging yields 0 = c2 24c 92. Solving this quadratic gives c= 24 2 944 24 4 59 = = 12 2 59. 2

However, the question calls for c > 0, so the only possible value of c is 12 + 2 59, because 12 = 144 < 236 = 2 59. Plugging this value of c into the equation for f (x) and nding its complex roots using the cubic formula and plugging these roots into the given relation veries that the relation is indeed satised, so c = 12 + 2 59 (we can also note that no irreversible steps were taken rather than verify in such a foolish way). Page 1 of Problem 3

Student: Sitan Chen Username: Math Geek ID#: 10636

USA Mathematical Talent Search

Year 22

Round 1

Problem 4

Without loss of generality, we will say that Charlie chooses the tangent AB shown in the below diagrams (note that this preserves generality because reecting the entire diagram through O1 O2 gives us the case for the other common tangent). Given this, we split the problem into two cases: C is the intersection point between the two circles that is closer to AB, and C is the one farther from AB. Case 1: C is the intersection point of Sashas circle and Rebeccas circle that is closer to AB. Call the center of Sashas circle center O1 and the center of Rebeccas circle center O2 . Draw the perpendicular bisector of AC and the perpendicular bisector of BC, and label their intersection point O3 , which is also the circumcenter of triangle ABC. Denote the midpoint of AC to be M1 and the midpoint of BC to be M2 .

Note that because AM1 = CM1 , the arc that AO1 M1 intercepts is equal to half of the measure of circle O1 s minor arc AC. However, because AB is tangent to circle O1 , BAC is one half the measure of minor arc AC as well, so AO1 O3 = AO1 M1 = BAC. Similarly, because BM2 = CM2 , the arc that BO2 M2 intercepts is equal to half of the measure of circle O2 s minor arc BC. Because AB is tangent to circle O2 , ABC is one half of the measure of minor arc BC as well, so BO2 O3 = BO2 M2 = ABC. Note that because AM1 = CM1 , AO3 M1 intercepts an arc on circle O3 with a measure of half of circle O3 s minor arc AC, while ABC is the inscribed angle of that minor arc, so ABC = AO3 O1 . Similarly, we can prove that because BM2 = CM2 , BO3 M2 intercepts an arc on O3 with a measure of half of circle O3 s minor arc BC, and because BAC is an inscribed angle of minor arc BC, BAC = BO3 O2 .

Page 1 of Problem 4

Student: Sitan Chen Username: Math Geek ID#: 10636 Thus, O3 AO1

USA Mathematical Talent Search

O2 BO3 , so O3 A O1 A = . O2 B O3 B

Year 22

Round 1

Problem 4

Substituting in known values of the radii of Sashas and Rebeccas circles and cross-multiplying, we get (O3 A)(O3 B) = rs. However, O3 A and O3 B are both equal to the radius of O3 , which we will call t. Then t2 = rs t = rs. Therefore, the radius of Charlies circle is constant, because r and s are constant in this case. Case 2: C is the intersection point of Sashas circle and Rebeccas circle that is farther from AB. Note that the above proof of case 1 applies word for word to this choice of intersection point as well, but for the readers interest and convenience, we will include it below as well. Again, call the center of Sashas circle center O1 and the center of Rebeccas circle center O2 . Draw the perpendicular bisector of AC and the perpendicular bisector of BC, and label their intersection point O3 , which is also the circumcenter of triangle ABC. Denote the midpoint of AC to be M1 and the midpoint of BC to be M2 .

Note that because AM1 = CM1 , the arc that AO1 M1 intercepts is equal to half of the measure of circle O1 s minor arc AC. However, because AB is tangent to circle O1 , BAC is one half the measure of minor arc AC as well, so AO1 O3 = AO1 M1 = BAC. Similarly, because BM2 = CM2 , the arc that BO2 M2 intercepts is equal to half of the measure of circle O2 s minor arc BC. Because AB is tangent to circle O2 , ABC is one half of the measure of minor arc BC as well, so BO2 O3 = BO2 M2 = ABC. Note that because AM1 = CM1 , AO3 M1 intercepts an arc on circle O3 with a measure of half of circle O3 s minor arc AC, while ABC is the inscribed angle of that minor arc, so ABC = AO3 O1 . Similarly, we can prove that because BM2 = CM2 , BO3 M2 intercepts an arc on O3 with a measure of half of circle O3 s minor arc BC, and because BAC is an inscribed angle of minor arc BC, BAC = BO3 O2 .

Page 2 of Problem 4

Student: Sitan Chen Username: Math Geek ID#: 10636 Thus, O3 AO1

USA Mathematical Talent Search

O2 BO3 , so O3 A O1 A = . O2 B O3 B

Year 22

Round 1

Problem 4

Substituting in known values of the radii of Sashas and Rebeccas circles and cross-multiplying, we get (O3 A)(O3 B) = rs. However, O3 A and O3 B are both equal to the radius of O3 , which we will call t. Then t2 = rs t = rs. Therefore, the radius of Charlies circle is constant, because r and s are constant in this case. Thus, the radius of Charlies circle is independent of the location of Sashas and Rebeccas circles and of Charlies choice of tangent and is always equal to the geometric mean of the radius of Sashas circle and the radius of Rebeccas circle.

Page 3 of Problem 4

Student: Sitan Chen Username: Math Geek ID#: 10636

USA Mathematical Talent Search

Year 22

Round 1

Problem 5

Without loss of generality, label the polygon P s vertices, clockwise, as P1 , P2 , ..., Pn . Note that on a regular n-sided polygon, for AOB to equal 2k , the chord AB must intercept n an arc that contains, not including A and B, k 1 other vertices of the regular polygon. Next, note that if a peculiar polygons vertices are a subset of a regular polygon with an even 2( n ) 2 number of sides, then the quantity n = will be the measure of exactly one AOB. However, in this case vertices A and B must be diametrically opposite on the circumcircle of the regular polygon whose vertices include those of P , in which case the center O will lie in P or on its perimeter, violating condition b. Therefore, a peculiar polygons vertices must be a subset of the vertices of a polygon with an odd number 2m + 1 of sides. Finally, note that if we draw a chord connecting any two vertices of a regular polygon, then it will split the polygon into two polygons: one whose circumcenter lies outside of itself and one whose circumcenter lies inside of itself. Obviously, any polygon whose vertices are a subset of the formers will not contain the center O of the regular polygon. The largest such polygon that is formed by dissecting the regular 2m + 1-gon into two with a chord and that does not contain O, is congruent to the one with vertices, in clockwise order, of P1 , P2 , ..., Pm+1 . Now consider condition c. For a 2m + 1-gon to contain a peculiar polygon, there must exist an angle AOB for 0 < k = m < 2m+1 equal to 2m , which by an earlier conclusion is equivalent to the 2 n angle between two vertices separated by m 1 vertices in between on the original regular polygon. Indeed, there must exist an angle separated by any number of vertices from 0 to m 1, inclusive. In other words, two vertices Pi and Pi+k must exist for all values of k from 1 to m, inclusive. For simplicity, we will identify all polygons by the clockwise sequence of indices of their vertices Pi . Consider the sequence of indices 1, 2, 3,..., m + 1. Note that the maximum possible dierence j is m, so if peculiar polygon P has exactly j vertices, then 2 must equal m. This is necessary and sucient for each possible positive dierence from 1 to m to be represented by exactly one positive j dierence between two vertices indices, because if 2 < m, there are fewer than m values that a j positive dierence between two indices can take on, and if 2 > m, there must exist at least one value from 1 to m represented by more than one positive dierence between two indices. j Thus, the sequence of indices is equivalent to 1, 2, 3,..., 2 + 1. Now we begin testing values of j, where, because P is a polygon, j 3. For each j, we want to choose j terms from the sequence j j 1, 2, 3,..., 2 + 1 so that each dierence from 1 to 2 , inclusive, is represented by exactly one pair j of terms from the sequence. Note that in each case, 1 and 2 + 1 must be terms, because they form j the only pair of terms whose positive dierence is 2 . Furthermore, note that if two sequences of terms/indices denoting a peculiar polgyon are such that if you placeone in ascending order and the other in descending order, corresponding terms add up to m + 2, then they are merely reections of each other and are thus congruent. For j = 3, m + 1 = 3 + 1 = 4, and we must choose 1 and 4, accounting for the dierence 2 of 3. Next, we can choose 2 or 3, but the sequences (1, 2, 4) and (1, 3, 4) are equivalent because corresponding terms in sequences (1, 2, 4) and (4, 3, 1) add up to 5 = m + 2, and it is not hard to see that the polygons these two sequences denote are reections of each other. Thus, there is only one 3-sided peculiar polygon. For j = 4, m + 1 = 4 + 1 = 7, and we must choose 1 and 7, accounting for the dierence of 2 6. We can only achieve a dierence of 5 with 6-1 or 7-2, so we can either pick 2 or 6. Without Page 1 of Problem 5

Student: Sitan Chen Username: Math Geek ID#: 10636

USA Mathematical Talent Search

Year 22

Round 1

Problem 5

loss of generality, pick 2 because the polygon resulting from picking 6 is merely the reection of the polygon resulting from picking 2. Because 2 also gives us the dierence 2-1=1, we cannot pick 6 or 3, or we have another 1=7-6=3-2, so we can only choose from 4 or 5. We want a dierence of 4, and the only term that gives us that is 5, where 5-1=4. It is not hard to see that all terms are represented (2-1=1, 7-5=2, 5-2=3, 5-1=4, 7-2=5, 7-1=6). Thus, there is only one 4-sided peculiar polygon, from the sequence of (1, 2, 5, 7). For j 5, consider the sequence 1, 2, 3, 4, 5, 6,..., m 4, m 3, m 2, m 1, m, m + 1 (note that because j 5, m + 1 5 + 1 = 11, so m 4 6). By the same logic as in the 2 last case, 1, 2, and m + 1 must be chosen, giving us the dierences of 1, m, and m 1 and thus eliminating the possibility of choosing 3 or m. To get dierence m 2, we must choose m 1 so that (m 1) 1 = m 2, eliminating 4, m 2, and m 3. This term also gives us dierence m 3 = (m 1) 2 and dierence 2 = (m + 1) (m 1). To get the dierence m 4, we know 1 + (m 4) = m 3, 2 + (m 4) = m 2 and (m 1) (m 4) = 3 have been eliminated as possible terms, but (m + 1) (m 4) = 5 has not been, so we have to choose this term. This also gives dierence 3 = 5 2, so we can eliminate m 4 = (m 1) 3 along with 6 = 5 + 1 (as dierence 1 has already been covered). These two terms happen to be the same term for j = 5, where m = 10. At this point, among the terms 1, 2, 3, 4, 5, 6, m 4, m 3, m 2, m 1, m + 1, for j 5, we know for certain that 1, 2, 5, m 1, and m + 1 are the only terms that we can choose, while 3, 4, m 4, m 3, m 2, and m have been eliminated as possible choices. The only pairs of terms with positive dierence m 5 are (1,m 4), (2,m 3), (3,m 2), (4,m 1), (5,m), and (6,m + 1). However, notice that in each of these ordered pairs, there exists at least one term that we have eliminated as a possible term to choose, so the dierence of m 5 cannot exist. Thus, for j 5, no such sequences of indices dening a peculiar polygon exist. Thus, there are only 2 non-congruent peculiar polygons.

Page 2 of Problem 5

Student: Sitan Chen Username: Math Geek ID#: 10636

USA Mathematical Talent Search

Year 22

Round 1

Problem 6

In general, call such a game involving n people and n dierent presents a n-game. a) We claim that the ideal strategy is that for a general n-game, for each k from 1 to n, inclusive, if and only if there is a present that has not been revealed that is less than the maximum dollar amount among the available gifts that have been opened, player k should swap with the person holding an open present with that maximum dollar amount. Induct backwards starting with Pn . Obviously, after players from 1 to n 1 have revealed all of their presents contents in some way, he knows what dollar amount is inside the gift that he holds, so he will swap his present with the person with the maximum available open present if he knows his present is less than that. However, he will open his present if he knows his present is greater than the maximum available open present. In this case, Pn has followed the stated strategy because if and only if there exists a dollar amount that has not been revealed that is less than the maximum open available present does he swap with the person with that maximum present. Now assume that we know that person Pk+1 follows this strategy. We have to prove both parts of the strategy are ideal for Pk . We rst prove that if there exists an unopened present with less money than the maximum open available present, then the best strategy for Pk is to swap with the holder of that present. Note that in all cases, if Pk chooses to swap with the person with an open present of x dollars, he leaves the game with x dollars. If his initial present contains an amount y less than x and he chooses to open his present, then based on our induction hypothesis, no player that goes after him that wishes to switch will switch with him. Thus, Pk is stuck with y < x dollars, so the proposed strategy gives the maximum amount of money. If his initial present, on the other hand, contains an amount y greater than x, then if he opens his present, he will give later players a new maximum open present amount to swap with and keep. By our induction hypothesis, Pk+1 will then swap with Pk , giving Pk a new present less than x. If this new present amount is less than x, he ends ups with less than x dollars, as later players will switch with other players with higher open present amounts. However, if this new present amount is greater than x, than players after Pk+1 will continue to swap there own unopened presents with Pk until Pk ends up with a present less than x. Indeed, such an unopened present necessarily exists among Pk+1 to Pn based on our initial condition that Pk swaps if and only if such an unopened present exists that has an amount less than the maximum among the opened presents. Thus, in all cases, if Pk chooses to keep his present even though such an unopened present exists, he will end up with less money than he would if he swapped with the holder of x dollars and left the game. Next, we prove that if there does not exist an unopened present with less money than the maximum open present x, then the best strategy for Pk is to open his own present. In other words, if the unopened presents are known to all be greater than the maximum open present amount, then Pk s best strategy is to open his present. Note that if he follows this strategy, he will open a present with more than x dollars, and by our induction hypothesis, subsequent players will follow the proposed strategy and swap with his present. Among the presents that the players from Pk to Pn inclusive begin with, the lowest possible value is still greater than x in this case, so Pk , after any number of swaps with later players, will still end up with a present amount of more than x if he merely opens his own present during his turn. On the other hand, if he swaps with the player with x dollars and leaves the game, he ends up with only x dollars, so the strategy of opening his

Page 1 of Problem 6

Student: Sitan Chen Username: Math Geek ID#: 10636

USA Mathematical Talent Search

Year 22

Round 1

Problem 6

own present on his turn, in the case that there does not exist an unopened present with less money than the maximum open present x, is the ideal strategy. Therefore, if Pk+1 follows the proposed strategy, Pk must also follow the strategy, and because Pn follows the strategy, it is indeed followed by every player in the game. Thus, we have proved the strategy to be optimal for all such games with n people and n presents. b) To nd the expected number of swaps, we induct on the number n of people and presents involved in the game. We claim that the expected number Nn of swaps is equal to
n i=1

i1 . i

For base case n = 1, obviously, player 1 has no choice but to open his present, as he has no one to swap with, contributing an expected value of 0 swaps, as desired. Assume that for a game with k people and k presents, that the expected value of swaps is
n i=1

i1 . i

Then consider a game with k + 1 people and k + 1 presents. Obviously, P1 has no say in the matter, opens his present, and contributes 0 swaps in all cases. However, if P1 s present is 1 dollar, the subsequent presents consist of all presents from 2 dollars to k + 1 dollars, inclusive but not necessarily in that order. We already know that later players will follow an ideal strategy, so player 2 will open his present, and subsequent players, if they swap, will not swap with P1 . Thus, we can ignore P1 and each present from 2 dollars to k + 1 dollars, inclusive, by its index in relation to the other presents, that is, 2 dollars becomes 1 because it is the least present amount, 3 dollars becomes 2 because it is the second-least present amount, 4 dollars becomes 3 because it is the third-least present amount, and so on. Ignoring 1 leaves us with k people and k presents, and because we know that later players will not swap with 1, the present 1 indices represent dollar amounts in a k-game. This case occurs with k+1 probability and consists of Nk swaps. Thus, this case contributes Nk k+1 swaps. In the same k + 1-game, if P1 s present is more than 1 dollar, P1 must switch with P2 based on the ideal strategy. Then P2 leaves the game after contributing 1 swap, and we are left with k players. P1 s forced exchange with P2 leaves him with a new value that is equivalent to P1 s opening his own present at the start of a k-game to get that value. Let this new value be u dollars. Now assign the remaining unopened presents values based on their indices as we did in the previous case, except in this case, these indices span from 1 to k + 1, inclusive, with the exception of u. Note again that these indices represent dollar amounts in a k-game, so after P2 leaves, we are again left with a k-game scenario. Because this case, that P1 s present is more than 1 dollar, occurs with k probability k+1 , and because P2 contributes an additional 1 swap, this case contributes k (1 + Nk ) k+1 Page 2 of Problem 6

Student: Sitan Chen Username: Math Geek ID#: 10636 .

USA Mathematical Talent Search

Year 22

Round 1

Problem 6

Thus, overall, the expected number of swaps in a k + 1 game is Nk+1 = Nk k 1 k k k + (1 + Nk ) = Nk ( + )+ = Nk + = k+1 k+1 k+1 k+1 k+1 k+1
k+1 i=1

i1 . i

This completes our induction. The expected number of swaps for a 50-game is thus N50 = 1 2 3 49 + + + + . 2 3 4 50

For the readers interest, this number happens to be 141008987635075780359241 45.501. 3099044504245996706400

Page 3 of Problem 6