CHAPTER 3: NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS

I.

EULERS METHOD

For the general initial value problem:

dy = f ( x, y ); when x = xo, y = yo, dx

The sequence of approximations are expressed in terms of the recurrence relations

x k +1 = x k + h

y k +1 = y k + hf ( x k , y k ) , y

for k = 0, 1, 2, . Where h = x .

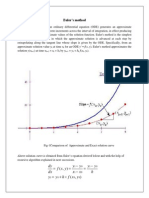
(x,y) dx = x

y dy

The above figure shows the geometrical significance of the differential dy and of y , the actual change in y, as induced by an increment dx ( or x ) applied to x. Example 3.1: Obtain the solution of the differential equation y = y2 x2 for which y =1 when x = 0. Approximate the solution y = f(x) in the interval 0 < x < . Exercise 3.1: Apply Eulers Method to approximate the solution of the initial value problem in the given interval. y = x + y; when x = 0, y = 1; x = 0.1 and 0 < x < 1.

II. A Method of Successive Approximation This method is based on the following theorem. Existence Theorem : If f(x,y) is sufficiently well behaved near the point (x0,y0), the differential equation has a solution that passes through the point (x0,y0) and that solution is unique near (x0,y0). The solution is in the form of a sequence of functions which has a limit and that the limiting function is the desired solution. The sequence is defined as follows:

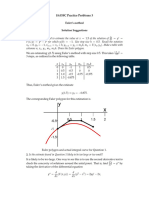
Example 3.2 :

Apply the method to the problem, with y desired in the interval . and the

Solution: The desired solution is sequence of functions is given by

where and for n > 1,

Then, can be obtained in a similar manner. See excel notes for the comparison of values of .

An improvement on the Method of Successive Approximation The method alters the initial approximation by choosing to have the correct slope at the initial conditions of x and y. In the previous problem at x = 0, the slope is y = 1. Hence we choose and proceed to compute , as before. The successive stages of approximation to y(x) now become

Values of

are shown in the table .

Exercise 3.2: Apply the method of this section to the problem, Obtain y3(x) and y4(x). III. Taylors Theorem Initial Value Problem: y = F(x,y); x = x0, y = y0.

Approximation Formula: Estimated Error: .

Example 3.3: Use Taylors Theorem to approximate the value of y in Example 3.1. Exercise 3.3: Use Taylors Theorem to approximate the the values of y accurately to two decimal places on the given interval using the the prescribed increment in x. Retain powers of x x0 sufficiently large. x = 0.1 and 0 < x < 0.5.

IV. The Runge-Kutta Method

The method requires the computation of a single function at several points rather than the computation of several different functions at a single point. Initial Value Problem: Notation: Fn = F (xn, yn ) Equation: The value of at x = xn + h is Where y = F(x,y); x = xn, y = yn,

Example 3.4 Solve Example 3.1 by Runge-Kutta Method. Use x = 0.1 and x = 0.2. Exercise 3.4: Continue the computation of Example 3.4 to obtain the approximate values of y for x = 0.3, 0.4 and 0.5.