Documenti di Didattica
Documenti di Professioni
Documenti di Cultura
Chapter 4
Caricato da
jpatrickmaguireDescrizione originale:
Copyright
Formati disponibili
Condividi questo documento
Condividi o incorpora il documento
Hai trovato utile questo documento?
Questo contenuto è inappropriato?
Segnala questo documentoCopyright:
Formati disponibili
Chapter 4
Caricato da
jpatrickmaguireCopyright:
Formati disponibili
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
March 3, 2007
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Function
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Lemma 4.1
Lemma 4.1 Given relatively prime integers a and m, there exists an integer b, unique modulo m, such that a b 1 (mod m).
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Lemma 4.1
Lemma 4.1 Given relatively prime integers a and m, there exists an integer b, unique modulo m, such that a b 1 (mod m). Denition If a b 1 (mod m), then we say that b is the inverse of a modulo m.
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Proof of Lemma 4.1
Proof of Lemma 4.1 By the Euclidean algorithm (Algorithm 1.8) we can nd integers b and c such that a b + m c = 1. This means that a b is congruent to 1 modulo m. Let e be any other integer satisfying a e 1 (mod m).
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Proof of Lemma 4.1 - Cont.
Proof of Lemma 4.1 - Cont. Then, e e (a b) (mod m) (a e) b (mod m) b (mod m)
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Function
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Chinese Remainder Theorem
We need to prove that if p and q are distinct primes, then (p q) = (p 1) (q 1).
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Chinese Remainder Theorem
We need to prove that if p and q are distinct primes, then (p q) = (p 1) (q 1).
We will prove more. The starting point is an algorithm that appeared in the rst century A.D. simultaneously in China, in the writings of Sun-Tsu, and in Judea, in a book by Nichomachus of Gerasa.
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Chinese Remainder Theorem
Theorem 4.4 Let m1 , m2 , . . . , mr be positive integers that are pairwise relatively prime (i.e., no two share a common factor larger than one). Let a1 , a2 , . . . , ar be arbitrary integers. Then there exists an integer a such that a a1 (mod m1 ) a2 (mod m2 ) . . . ar (mod mr ). Furthermore, a is unique modulo M = m1 m2 mr .
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Proof of Theorem 4.4
Proof of Theorem 4.4 We will actually nd an algorithm for constructing a. For each i from 1 up to r , dene Mi by Mi = (M/mi )(mi ) . Since M/mi is relatively prime to mi and divisible by mj for every j not equal to i, we have that Mi Mj for every j not equal to i. 1 (mod mi ) 0 (mod mi )
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Proof of Theorem 4.4 - Cont.
Proof of Theorem 4.4 - Cont. Dene a by a = a1 M1 + a2 M2 + + ar Mr .
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Proof of Theorem 4.4 - Cont.
Proof of Theorem 4.4 - Cont. Dene a by a = a1 M1 + a2 M2 + + ar Mr . To see that a is unique modulo M, let b be any other integer satisfying the r congruences. Then for each mi , a and b are congruent modulo mi . In other words, mi divides b a. Since this is true for every i, M divides b a which means that ab (mod M).
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Proof of Theorem 4.4 - Cont.
Proof of Theorem 4.4 - Cont. Dene a by a = a1 M1 + a2 M2 + + ar Mr . To see that a is unique modulo M, let b be any other integer satisfying the r congruences. Then for each mi , a and b are congruent modulo mi . In other words, mi divides b a. Since this is true for every i, M divides b a which means that ab (mod M).
Of course, one need only compute the values of Mi modulo M, which keeps the computations a little more reasonable.
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Function
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Question
What if two or more of the moduli are divisible by the same prime? The Chinese Remainder Theorem does not work in this case.
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Question
What if two or more of the moduli are divisible by the same prime? The Chinese Remainder Theorem does not work in this case. We rst observe that if we have a congruence with a modulus which is divisible by more than one prime, then we can split our single congruence into several congruences as long as the new moduli are relatively prime and their product is the original modulus.
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Example
Example x 3 (mod 45)
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Example
Example x 3 (mod 45) is equivalent to x 3 (mod 5) and x 3 (mod 9).
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Example
Example x 3 (mod 45) is equivalent to x 3 (mod 5) and x 3 (mod 9).
The equivalence is a consequence of the Chinese Remainder Theorem.
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Procedure and Example
Procedure Let us assume that in our system of congruences we have two moduli say m1 and m2 that are both divisible by the same prime p.
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Procedure and Example
Procedure Let us assume that in our system of congruences we have two moduli say m1 and m2 that are both divisible by the same prime p. We split each of our congruences into two congruences as explained above where one of the new moduli is the highest power of p dividing m1 or m2 , respectively.
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Procedure and Example
Procedure Let us assume that in our system of congruences we have two moduli say m1 and m2 that are both divisible by the same prime p. We split each of our congruences into two congruences as explained above where one of the new moduli is the highest power of p dividing m1 or m2 , respectively. Example As an example, the two congruences x x 3 (mod 45) 7 (mod 756)
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Example - Cont.
Example - Cont. are split into four congruences: x x x x 3 (mod 9) 7 (mod 27) 3 (mod 5) 7 (mod 28).
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Example - Cont.
Example - Cont. are split into four congruences: x x x x 3 (mod 9) 7 (mod 27) 3 (mod 5) 7 (mod 28).
We now have two congruences that both involve powers of p. One of two things has to happen:
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Two Things
Two Things 1. The congruences are contradictory and so there are no solutions. This is the case with the example given above. If x 3 (mod 9), then x 3, 12, or 21 (mod 27). or
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Two Things
Two Things 1. The congruences are contradictory and so there are no solutions. This is the case with the example given above. If x 3 (mod 9), then x 3, 12, or 21 (mod 27). or 2. Both of the congruences for powers of p are implied by the congruence with the higher power. This means we can get rid of one of our equations, leaving us with three congruences with relatively prime moduli for which we can use the Chinese Remainder Theorem.
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Example
Example Consider the system of congruences, x x 7 (mod 200) 82 (mod 375).
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Example
Example Consider the system of congruences, x x 7 (mod 200) 82 (mod 375).
This splits into four congruences: x x x x 7 (mod 25) 82 (mod 125) 7 (mod 8) 82 (mod 3).
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Example - Cont.
Example - Cont. The congruence modulo 25 is a special case of the congruence modulo 125, so we really have three congruences to relatively prime moduli:
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Example - Cont.
Example - Cont. The congruence modulo 25 is a special case of the congruence modulo 125, so we really have three congruences to relatively prime moduli: x x x 82 (mod 125) 7 (mod 8) 82 1 (mod 3),
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Example - Cont.
Example - Cont. The congruence modulo 25 is a special case of the congruence modulo 125, so we really have three congruences to relatively prime moduli: x x x 82 (mod 125) 7 (mod 8) 82 1 (mod 3),
which has as a solution x 1207 (mod 3000).
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Function
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Lemma 4.6
Lemma 4.6 If gcd(m, n) = 1, then (m n) = (m) (n).
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Lemma 4.6
Lemma 4.6 If gcd(m, n) = 1, then (m n) = (m) (n). Proof Let a be a positive integer less than and relatively prime to m n. In other words, a is one of the integers counted by (m n).
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Lemma 4.6
Lemma 4.6 If gcd(m, n) = 1, then (m n) = (m) (n). Proof Let a be a positive integer less than and relatively prime to m n. In other words, a is one of the integers counted by (m n). We consider the correspondence a (a mod m, a mod n).
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Proof of Lemma 4.6 - Cont.
Proof of Lemma 4.6 - Cont. The integer a is relatively prime to m and relatively prime to n, so a mod m and a mod n are relatively prime to m and n, respectively.
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Proof of Lemma 4.6 - Cont.
Proof of Lemma 4.6 - Cont. The integer a is relatively prime to m and relatively prime to n, so a mod m and a mod n are relatively prime to m and n, respectively. This means that each integer counted by (m n) corresponds to a pair of integers, the rst counted by (m) and the second counted by (n).
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Proof of Lemma 4.6 - Cont.
Proof of Lemma 4.6 - Cont. By the second part of Theorem 4.4, distinct integers counted by (m n) correspond to distinct pairs. Therefore, (m n) is at most the number of such pairs: (m n) (m) (n).
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Proof of Lemma 4.6 - Cont.
Proof of Lemma 4.6 - Cont. By the second part of Theorem 4.4, distinct integers counted by (m n) correspond to distinct pairs. Therefore, (m n) is at most the number of such pairs: (m n) (m) (n). In the other direction, we take a pair of integers, one counted by (m) and the other counted by (n). Since m and n are relatively prime, we can use the rst part of Theorem 4.4 to construct a unique positive integer a less than and relatively prime to m n.
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Proof of Lemma 4.6 - Cont.
Proof of Lemma 4.6 - Cont. By the Chinese Remainder Theorem (b, c) a b (mod m) and c (mod n).
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Proof of Lemma 4.6 - Cont.
Proof of Lemma 4.6 - Cont. By the Chinese Remainder Theorem (b, c) a b (mod m) and c (mod n).
So the number of such pairs is at most (m n): (m n) (m) (n).
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Proof of Lemma 4.6 - Cont.
Proof of Lemma 4.6 - Cont. By the Chinese Remainder Theorem (b, c) a b (mod m) and c (mod n).
So the number of such pairs is at most (m n): (m n) (m) (n). In Exercise 4.17 you are asked to prove that if p is a prime, then (pa ) = pa1 (p 1).
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Theorem 4.7
With this equality and Lemma 4.6, we can calculate (n) for n that we can factor.
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Solving Linear Congruences Chinese Remainder Theorem Moduli are not Relatively Prime Properties of Eulers Functio
Theorem 4.7
With this equality and Lemma 4.6, we can calculate (n) for n that we can factor. Theorem 4.7 Let
a a a n = p11 p22 pr r
be the unique factorization of n. Then (n) = n 1 1 p1 1 1 p2 1 1 pr .
Chapter 4 - Solving Linear Congruences, Chinese Remainder Theorem, and Eulers Function
Potrebbero piacerti anche
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeDa EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeValutazione: 4 su 5 stelle4/5 (5795)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreDa EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreValutazione: 4 su 5 stelle4/5 (1091)
- Never Split the Difference: Negotiating As If Your Life Depended On ItDa EverandNever Split the Difference: Negotiating As If Your Life Depended On ItValutazione: 4.5 su 5 stelle4.5/5 (838)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceDa EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceValutazione: 4 su 5 stelle4/5 (895)
- Grit: The Power of Passion and PerseveranceDa EverandGrit: The Power of Passion and PerseveranceValutazione: 4 su 5 stelle4/5 (588)
- Shoe Dog: A Memoir by the Creator of NikeDa EverandShoe Dog: A Memoir by the Creator of NikeValutazione: 4.5 su 5 stelle4.5/5 (537)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersDa EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersValutazione: 4.5 su 5 stelle4.5/5 (345)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureDa EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureValutazione: 4.5 su 5 stelle4.5/5 (474)
- Her Body and Other Parties: StoriesDa EverandHer Body and Other Parties: StoriesValutazione: 4 su 5 stelle4/5 (821)
- The Emperor of All Maladies: A Biography of CancerDa EverandThe Emperor of All Maladies: A Biography of CancerValutazione: 4.5 su 5 stelle4.5/5 (271)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)Da EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Valutazione: 4.5 su 5 stelle4.5/5 (121)
- The Little Book of Hygge: Danish Secrets to Happy LivingDa EverandThe Little Book of Hygge: Danish Secrets to Happy LivingValutazione: 3.5 su 5 stelle3.5/5 (400)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyDa EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyValutazione: 3.5 su 5 stelle3.5/5 (2259)
- The Yellow House: A Memoir (2019 National Book Award Winner)Da EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Valutazione: 4 su 5 stelle4/5 (98)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaDa EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaValutazione: 4.5 su 5 stelle4.5/5 (266)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryDa EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryValutazione: 3.5 su 5 stelle3.5/5 (231)
- Team of Rivals: The Political Genius of Abraham LincolnDa EverandTeam of Rivals: The Political Genius of Abraham LincolnValutazione: 4.5 su 5 stelle4.5/5 (234)
- On Fire: The (Burning) Case for a Green New DealDa EverandOn Fire: The (Burning) Case for a Green New DealValutazione: 4 su 5 stelle4/5 (74)
- The Unwinding: An Inner History of the New AmericaDa EverandThe Unwinding: An Inner History of the New AmericaValutazione: 4 su 5 stelle4/5 (45)
- Euclidean Distance MatrixDocumento8 pagineEuclidean Distance MatrixManahil ShaikhNessuna valutazione finora
- mpm2d1 Course Overview 2017Documento2 paginempm2d1 Course Overview 2017api-235072058Nessuna valutazione finora
- 2 Sampling and Sampling TechniquesDocumento73 pagine2 Sampling and Sampling TechniquesJozen RyanNessuna valutazione finora
- SME3013 History of Mathematical Sciences: SEMESTER 1 SESSION 2019/2020Documento2 pagineSME3013 History of Mathematical Sciences: SEMESTER 1 SESSION 2019/2020Nur Hana SyamsulNessuna valutazione finora
- 'Work in Progress' - Analysing Nono's 'Il Canto Sospeso'Documento57 pagine'Work in Progress' - Analysing Nono's 'Il Canto Sospeso'iuhalsdjvauhNessuna valutazione finora
- Tips For PhiLSAT TakersDocumento3 pagineTips For PhiLSAT TakersChristian VenusNessuna valutazione finora
- Unit 2Documento44 pagineUnit 2nagpal3Nessuna valutazione finora
- Various A-Level Economics NotesDocumento7 pagineVarious A-Level Economics NotesYasheelNessuna valutazione finora
- Markov Interest Rate Models - Hagan and WoodwardDocumento28 pagineMarkov Interest Rate Models - Hagan and WoodwardlucaliberaceNessuna valutazione finora
- The Neural StrategyDocumento102 pagineThe Neural StrategyGoran Stevanovic50% (2)
- Engineering Mathematics IIDocumento102 pagineEngineering Mathematics IIIsaac P PlanNessuna valutazione finora
- 1 ToleranceDocumento42 pagine1 ToleranceDesalegn DgaNessuna valutazione finora
- Solving Accelerated Motion ProblemsDocumento23 pagineSolving Accelerated Motion ProblemsrhazoorNessuna valutazione finora
- Numericals SolutionDocumento6 pagineNumericals SolutionMenaka SrinivasanNessuna valutazione finora
- Statistics For Managers Using Microsoft Excel: 6 Global EditionDocumento53 pagineStatistics For Managers Using Microsoft Excel: 6 Global Edition015Devina UlimaNessuna valutazione finora
- ProbStat Lec05Documento21 pagineProbStat Lec05Nam KhanhNessuna valutazione finora
- WK 4 Intuitive Thinking and Strategic AnalysisDocumento10 pagineWK 4 Intuitive Thinking and Strategic AnalysisMARY LORD GERALDINE VELASCONessuna valutazione finora
- FX3 Programming ManualDocumento986 pagineFX3 Programming ManualPaulo Alexandra SilvaNessuna valutazione finora
- Go Math Homework 1st GradeDocumento7 pagineGo Math Homework 1st Gradeafnaewonaoejmm100% (1)
- All Subj 2 - Q3 - W4 - D2Documento9 pagineAll Subj 2 - Q3 - W4 - D2Salvacion DelfinNessuna valutazione finora
- Commutators in Quantum Mechanics PDFDocumento2 pagineCommutators in Quantum Mechanics PDFIsraelNessuna valutazione finora
- ParameterDocumento342 pagineParameterirving lopezNessuna valutazione finora
- Statics Module5Documento42 pagineStatics Module5Glenn Paul TalhaNessuna valutazione finora
- Human Errors Analysis and Safety Management SystemsDocumento48 pagineHuman Errors Analysis and Safety Management SystemsBambang ApriyantoNessuna valutazione finora
- PolygonsDocumento3 paginePolygonsHAMSKULLNessuna valutazione finora
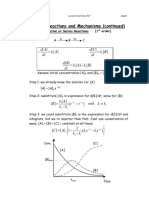
- Consecutive, Series, and Reversible ReactionsDocumento6 pagineConsecutive, Series, and Reversible ReactionsRojo JohnNessuna valutazione finora
- 3.5 Inverse Trig FunctionsDocumento6 pagine3.5 Inverse Trig FunctionsZazliana Izatti100% (1)
- 873p In003 - en PDocumento4 pagine873p In003 - en PdanielcelNessuna valutazione finora
- Chapter 4 Decision Support System (Dr. Mahmoud Mostafa)Documento32 pagineChapter 4 Decision Support System (Dr. Mahmoud Mostafa)JonathanHindiNessuna valutazione finora
- Gretl Ref A4 PDFDocumento226 pagineGretl Ref A4 PDFDianaNessuna valutazione finora