SELANGOR 2011

PAPER 2
1. Solve the simultaneous equations 3x y =
2 and x
2
+ 2y
2
xy = 4. Give the answers
correct to 3 decimal places.
[x = 1.159, y = 1.478, x = 0.216, y = 1.353]
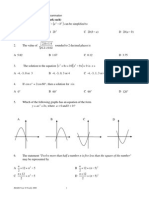
2. The diagram shows the graph of the
quadratic function y = f(x).

(a) Express the equation of f(x) in general
form.
(b) Find
(i) the minimum point of the function
by using the method of completing
the square,
(ii) the range of values of p such that
f(x) = p does not have real roots.
[(a) x
2
5x + 4 (b)(i)
5 9
,
2 4
| |

|
\ .

(ii) p <
9
4
]
3. The curve y = px
3
+ qx
2
+ r, where p, q are
r are constants, has a gradient function
6x(x 1) and passes through the point
(2, 9).
Find
(a) the value of p, q and r,
(b) the turning points of the curve.
[(a) p = 2, q = 3, r = 5 (b) (0, 5), (1, 4)]
4. (a) Sketch the graph of y = sin
3
2
x for
0 x 2t.
(b) Hence, using the same axes, sketch a
suitable straight line to find the
number of solutions for the equation
4tsin
3
2
x + 3x = 0 for 0 x 2t.
State the number of solutions.


5. The diagram shows a triangle OAB. The
straight line OM intersects the straight line
BL at N.

It is given OA = 3OL, AB = 2AM,
12 OA x =

and 8 OB y =

.
(a) Express in term of x

and/or y

(i) BL

(ii) OM

(b) It is given that ON hOM =

and
ON OL k LB = +

, where h and k are
constants. Find the value of h and of k.
[(a) (i) 4 8 x y

(ii) 6 4 x y +

(b) h =
1
2
, k =
1
4
]
6. The diagram shows the arrangement of the
first three of an infinite series of circles.
The first circle has a circumference of 50
cm. The circumference of each subsequent
circle is half of the circumference of the
pervious circle.

3 solutions
(a) Show the areas of the circle form a
geometric progression and state the
common ratio.
(b) Find the sum to infinity of the areas, in
cm
2
of all the circles, in terms of t.
[(a)
1
4
(b)
2500
3
]

SECTION B
7. The diagram shows the straight line PQ and
the straight line y = 2 intersecting the curve
y
2
= x 2 at point Q.

It is given that the area of the shaded region
is 12
2
3
unit
2
.
(a) Find the value of k.
(b) The region enclosed by the curve, the
straight line y = 2, the x-axis and the y-
axis is revolved through 360
o
about the
y-axis. Find the volume of revolution,
in terms of t.
[(a) 4 (b)
376
15
unit
3
]
8. The table shows the values of two viable, x
and y, obtained from an experiment. The
variables x and y are related by the equation
y = hk
x
, where h and k are constants.
x 1 2 4 6 8 10
y 6.92 9.8 19.4 37.4 74.0 144.4
(a) Plot log
10
y against x, using a scale of 1
cm to 1 unit on the x-axis and 10 cm to
1 unit on the log
10
y-axis. Hence, draw
the line of best fit.
(b) Use the graph in 8(a) to find the value
of
(i) h
(ii) k
(iii) x, when y = 50.
[(b) (i) 5.012 (ii) 1.4 (iii) 6.8]
9. The diagram shows a trapezium ABCD.
The line AB is perpendicular to the line AD.
It is given that the equation of AB is 3y x
6 = 0.

(a) Find
(i) the value of k,
(ii) the equation of the straight line
CD.
(b) The straight line CD is extended to a
point E such that CD : DE = 3 : 2.
Find
(i) the coordinates of E,
(ii) the area of triangle ODE.
(c) A point P(x, y) moves such that PB =
PD. Find the equation of the locus of P.
[(a) (i) 13 (ii) y =
1 13
3 3
x ]
10. The diagram shows a circle ABC with
centre O. BM and AMC are straight lines.

It is given that ZABC =
1
4
radians, BM =
10.24 cm and area of sector OAC is 9t cm
2
.
Calculate
[Use t = 3.142]
(a) the radius, in cm, of the circle,
(b) the perimeter, in cm, of sector OAC,
(c) the area, in cm
2
, of the shaded region.
[(a) 6 cm (b) 21.426 cm (c) 144.208
cm
2
]
11. (a) In a survey carried out in a school, 2
out of 5 teachers own laptops.
(i) If 6 teachers are selected at
random from the school, calculate
the probability that at most 2
teachers do not own a laptop.
(ii) There are 120 teachers in the
school. Calculate the mean and
standard deviation of the number
of teachers that own laptops.
(b) The time taken by a worker to travel
from his house to the workplace has a
normal distribution with a mean of 30
minutes and a variance of 81 minute
2
.
(i) Find the probability that a worker
chosen at random travels more
than 50 minutes.
(ii) If 70% of the time taken is less
than t minutes, find the value of t.
[(a) (i) 0.1792 (ii) = 48, = 28
(b) (i) 0.01321 (ii) 34.716]
SECTION C
12. The diagram shows a trapezium ABCD.
AB is parallel to DC.

Find
(a) ZADB,
(b) the length, in cm, of AC,
(c) the length, in cm, of BD,
(d) the area, in cm
2
, of triangle BCD.
[(a) 22
o
29' (b) 10.43 cm (c) 13.23 cm
(d) 45.53 cm
2
]

13. The table shows the price indices and
percentages of four items, P, Q, R and S,
used in the production of a type of popia.
Item Price
(RM)
in the
year
Price
(RM)
in the
year
Price
index
in the
year
2010
based
on
Percent
-age
(%)
2008 2010
2008
P 168 x 125 25
Q 150 125 120 m
R 105 100 105 n
S 90 99 y 40
(a) Find the value of x and of y.
(b) The composite index of the popia in
the year 2010 based on the year 2008 is
115. Find the value of m and of n.
(c) The composite index for the production
cost of the popia is expected to
increase by 20% from the year 2010 to
2012.
Calculate the composite index for the
production cost of popia in the year
2012 based on the year 2008.
[(a) x = 210, y = 110 (b) m = 20, n = 15
(c) 138]

14. A bakery plans to bake x number of
chocolate cakes and y number of layer
cakes in a day. The production of the cakes
is based on the following constraints:
I: The number of chocolate cakes is at
least 200 but does not exceed 500.
II: The total number of both cakes does
not exceed 700.
III: The number of chocolate cakes
exceeds 2 times the number of layer
cakes for at mot 200.
(a) Write three inequalities, other than x
0 and y 0 which satisfy all the above
constraints.
(b) Using a scale of 2 cm to 100 cakes on
both axes, construct and shade the
region R which satisfies all the above
constraints.
(c) Using the graph constructed in 14(b),
find
(i) the maximum number of layer
cakes that can be baked if the
bakery wants to bake 250
chocolate cakes.
(ii) the maximum profit per day if the
profit for each chocolate cake is
RM0.80 and the profit for each
layer cake is RM0.60.
[(a) 200 x 500, x + y 700, 2y x 200
(c) (i) 450 (ii) RM520 when x = 500, y =
200]
15. A particle moves in a straight line and
passes through a fixed point O. The
velocity of the particle, v cm s
-1
, is given by
v = 2t
2
t 6, where t is the time, in
seconds, after leaving O.
[Assume motion to the right as positive]
Find
(a) the initial velocity, in cm s
-1
, of the
particle,
(b) the minimum velocity, in cm s
-1
, of the
particle,
(c) the range of values of t during which
the particle moves to the right.
(d) the total distance, in cm, travelled by
the particle in the first 4 seconds.
[(a) 6 cm s
-1
(b)
49
8
cm s
-1
(c) t > 2
(d) 28 cm]