Documenti di Didattica
Documenti di Professioni
Documenti di Cultura
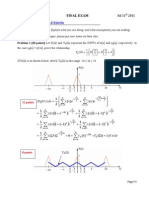
One Mark For Each Intercept Down Ward.: A A X y
Caricato da
Karabo MailulaTitolo originale
Copyright
Formati disponibili
Condividi questo documento
Condividi o incorpora il documento
Hai trovato utile questo documento?
Questo contenuto è inappropriato?
Segnala questo documentoCopyright:
Formati disponibili
One Mark For Each Intercept Down Ward.: A A X y
Caricato da
Karabo MailulaCopyright:
Formati disponibili
MAT171T Re-exam 2010A
1
Question 1
1.1 If
3
1
= a sketch the labeled graph of the function . 1 a x y + = Clearly
indicates all intercepts with axes. [3]
One mark for each , x intercept
|
.
|
\
|
|
.
|
\
|
0 ,
3
2
, 0 ;
3
4
, the last mark for shifting one unit
down ward.
1.2 Solve the following trigonometric equation: 0 tan sin 2 = + u u where | | t u ; 0 e
give your answer to 3 decimal places (radians). [6]
0
cos
sin
sin 2 = +
u
u
u
0 ) 1 cos 2 ( sin = + u u
2
1
cos = u or 0 sin = u
t t u
3
2
, , 0 =
MAT171T Re-exam 2010A
2
Question 2
2.1 Solve the following exponential equation for : x
[6]
( ) . 0 4 2 17 2
2 2
= +
+ x x
( ) . 0 4 2 17 2 2
2 2
= +
x x
Let
k
x
= 2
0 4 17 4
2
= + k k
( )( ) 0 4 1 4 = k k
4
1
= k
or
. 4 = k
2
2 2
=
x
or
2
2 2 =
x
2 = x
or
. 2 = x
2.2 Solve the following logarithmic equation for : x
( ) ( ) 3 3 log 1 log
2
= x x
x x
or
2
2
1 3 3
3 2 0
x x
x x
=
+ =
[5]
( )
( )
0
3 3
1
log
2
=
x
x
x
( )
( )
0
2
3 3
1
x
x
x
=
0 2 3
2
= + x x
( )( ) 0 1 2 = x x
2 = x or . 1 = x
MAT171T Re-exam 2010A
3
2.3 Given
1
1
2
2
+
=
x
x
e
e
y show that,
y
y
x
+
=
1
1
ln
2
1
[4]
( ) 1 1
2 2
= +
x x
e e y
x x
ye e y
2 2
1 = +
y
y
e
x
+
=
1
1
2
y
y
x
+
=
1
1
ln 2
y
y
x
+
=
1
1
ln
2
1
Question 3
3.1 Determine the first four terms using the Binomial expansion of the function
3
2
3
|
.
|
\
|
+
y
x . [5]
( ) ( )
( )( )
( )
( )( )( )
( )
3
0
2
2
2
2
2
3
2
3 ! 3
1 2 3
3 ! 2
2 3
3
3 |
.
|
\
|
+ |
.
|
\
|
+ |
.
|
\
|
+ =
y
x
y
x
y
x x
(one mark for each term)
3 2 2 4 6
27
1
3
1
y y x y x x + + + =
3.2 Give the exponential definition of ( ) x y 2 tanh = [1]
( )
( )
x x
x x
e e
e e
y
2 2
2 2
=
MAT171T Re-exam 2010A
4
Question 4
4.1 The velocity , v and the acceleration , a of a particle are given by k j i v + = 2 2
and . 2 3 5 k j i a + =
Calculate the angle between v and u
in degrees to 3 decimal places. [4]
( ) ( ) ( )
2 2 2
2 2 1
9 3
v = + +
= =
( ) ( ) ( )
38
2 3 5
2 2 2
=
+ + = a
( ) . 2 2 6 10 = = - a v
2
arccos
3 38
u
| |
=
|
\ .
83.791. u =
4.2 Show that the vector ( ) 1 ; 2 ; 2 = v and the vector ( ) 2 ; 4 ; 4 = u are parallel by
obtaining the vector product u v [3]
2 4 4
1 2 2
=
k j i
u v
4 4
2 2
2 4
1 2
2 4
1 2
k j i +
0 0 0 0 i j k = + + =
MAT171T Re-exam 2010A
5
Question 5
5. Given the matrix
(
(
(
=
1 3
5 2
4 1
D
Determine the following if possible, if not possible motivate your answer.
5.1 Calculate .
T
D D [3]
(
=
(
(
(
42 17
17 14
1 3
5 2
4 1
1 5 4
3 2 1
(one mark per row, one mark for the transpose)
5.2
( )
det
T
D D [1]
( )
det 14 42 17 17
299
T
D D =
=
5.3
T
D D
[2]
Impossible, they have different dimension
MAT171T Re-exam 2010A
6
5.4 Use matrix inversion to solve for y x, and z if:
1 3 3 2
0
1 2 2
= + +
=
= + +
x y z
z x y
z y x
[8]
(
(
(
=
(
(
(
(
(
(
1
0
1
2 3 3
1 1 1
2 2 1
z
y
x
(
(
(
=
2 3 3
1 1 1
2 2 1
A
( )
3 3
1 1
2
2 3
1 1
2
2 3
1 1
1 det
+
= A
12 2 5 =
9 =
Cofactor matrix
(
(
(
3 1 4
3 4 2
6 1 5
(one mark per row)
(
(
(
3 3 6
1 4 1
4 2 5
9
1
1
A
(
(
(
(
(
(
=
(
(
(
1
0
1
3 3 6
1 4 1
4 2 5
9
1
z
y
x
(
(
(
=
(
(
(
1
0
1
z
y
x
MAT171T Re-exam 2010A
7
5.5 Solve for y only using Cramers rule if:
5 3
0 3 2
3 2
= +
= +
= + +
z y x
z y x
z y x
[3]
1 3
3 2
2
1 3
1 2
1
1 1
1 3
1
1 1 3
1 3 2
2 1 1
+
=
. 29 = A
1 5 3
1 0 2
2 3 1
= A
y
5 3
3 1
1
1 3
2 1
0
1 5
2 3
2
=
. 0 =
. 0 =
A
A
=
y
y
Question 6
Determine
dx
dy
for the following functions and simplify where possible:
6.1 ( ) ( ) ( )
2 2 2
1 tan 1 sin 1 cos x x x y + + = [6]
( ) ( ) ( ) ( ) ( ) ( )( ) x x x x x x
dx
dy
2 1 sec 1 2 1 cos 1 sin 1 cos 2
2 2 2
+ + =
MAT171T Re-exam 2010A
8
6.2
( ) x x
x
y
+
=
1
1
3
[6]
3
1
ln ln
1
x
y
x x
=
+
1
2
1
ln ln 1 ln ln 1
3
y x x x = +
( ) ( )
'
1 1 1
3 1 2 1
y
y x x x
| |
=
|
|
+
\ .
( ) ( )
1 1 1
3 1 2 1
dy
y
dx x x x
| |
=
|
|
+
\ .
6.3
2 2
cot cosec x y y x = [6]
2 2 ' '
2 cot cosec 2 cosec cot x y x yy yy x x =
( )
' 2 2
cosec 2 cosec cot 2 cot y x y y x x x y =
'
2 2
cosec cot 2 cot
cosec 2
x x x y
y
x y y
+
=
+
MAT171T Re-exam 2010A
9
6.4 Determine all the critical (stationary) values of the function ( )
2
1 + = x x y [7]
( ) ( ) ( )
2 '
1 1 2 + + + = x x x y
( ) ( ) ( ) 0 1 1 2
2
= + + + x x x
( ) 0 1 = + x
0 1 3 = + x
1 = x
.
3
1
; = x
.
27
4
1
3
1
3
1
2
=
|
.
|
\
|
+ = y
( )
. 0
1 1 1
2
=
+ = y
The critical values are
|
.
|
\
|
27
4
;
3
1
and ( ) 0 ; 1
Alternatively we obtain:
( )
x x x
x x x y
+ + =
+ + =
2
1 2
3
2
1 4 3
2 '
+ + = x x y
( )( ) 0 1 1 3 = + + x x
1 = x
.
3
1
; = x
0 = y
.
27
4
; = y
The critical values are |
.
|
\
|
27
4
;
3
1
and ( ) 0 ; 1
MAT171T Re-exam 2010A
10
6.5 Investigate their nature (show all your calculations) [3]
4 6
2
2
+ = x
dx
y d
0 2
1
' '
< =
= x
y
0 2
3
1
' '
> =
= x
y
This implies that
|
.
|
\
|
27
4
;
3
1
is the minimum turning points and ( ) 0 ; 1 is the
maximum turning points.
6.6 Determine the coordinates of the point of inflection [3]
0 4 6 = + x
3
2
= x
.
27
2
1
3
2
3
2
2
=
|
.
|
\
|
+ = y
MAT171T Re-exam 2010A
11
Question 7 (Complex numbers)
7.1 Evaluate the following function (leave your answer in polar form to 2 decimal
places.)
7.1.1
( ) ( ) j j
cis
+ 1 2
30 2
2
[4]
( )( ) j j j 4 3 2 2 + = + +
( )( ) j j j + = + 7 1 4 3
7 50 8.13 j cis + =
( ) ( )
13 . 8 50
30 2
1 2
30 2
2
cis
cis
j j
cis
=
+
0.28 21.87 cis =
MAT171T Re-exam 2010A
12
7.2 Given the complex function
( )
2
1
1
j
z
+
= determine
z
z
(leave your answer in
rectangular form ( ) jy x + ) [5]
( )
j
j
z
2
1
1
1
2
=
+
=
j z
2
1
=
j z
2
1
=
|
.
|
\
|
|
.
|
\
|
|
.
|
\
|
|
.
|
\
|
=
j j
j j
z
z
2
1
2
1
2
1
2
1
Unnecessary step
4
1
4
1
=
. 0 1 j + =
7.3 Solve for x and y if
( ) y x
j x
jy
jx
3
4 3
1 +
+
=
+
[6]
( ) ( )( ) jy j x y x jx + + = + 1 4 3 3
2 2
4 4 3 3 3 yj j xjy x xyj jx + + + = +
( ) 1 0 4 3 = y x
( ) 2 4 3 3
2
+ = + xy xy x
From equation 2 we obtain
2 = x
Substitute x into ( ) 1 we obtain that .
2
3
= y
MAT171T Re-exam 2010A
13
Question 8 (Mensuration and Statistics)
8.1 Calculate the total exposed surface area of the figure accurately rounded to 2
decimal places. [5]
T cyl column sq
A A A A = +
2 2
2 2 4 2 ) r rh lh l t t = + +
( )
2
2 (20 ) 2 (20)(70) 4(10) 70 200 t t = + +
(r=20)
=2513.274+8796.459+2800-200
2
13909.73cm =
8.2 The area of a sector is 96 cm
2
. The angle at the centre is 170 u = , determine the
length of the radius of the circle accurately rounded to 3 decimal places. [5]
2
1
2
A r u =
96 A=
2
1
96 (2.967)
2
r =
2
64.71 r =
8.044 cm r =
MAT171T Re-exam 2010A
14
8.3 The table shows the distance travelled (in km) and the time taken (in days) of
eight construction trucks at the Gautrain project.
d 309 444 1912 687 895 1472 2160 220
t 3.5 1.0 4.5 1.0 2.5 3.0 4.5 1.0
8.3.1 Determine the equation of the linear regression line accurately rounded to 3
decimal places. [3]
4.575 387.409 d t
.
= +
8.3.2 Calculate the correlation coefficient to 3 decimal places. [2]
0.781 r =
Potrebbero piacerti anche
- Ath em Ati CS: L.K .SH Arm ADocumento10 pagineAth em Ati CS: L.K .SH Arm APremNessuna valutazione finora
- Seafield 2013 M1 (Q&A)Documento8 pagineSeafield 2013 M1 (Q&A)STPMmathsNessuna valutazione finora
- Advanced Inequations Exercise - 3Documento19 pagineAdvanced Inequations Exercise - 3Atul KumarNessuna valutazione finora
- NJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsDocumento10 pagineNJC JC 2 H2 Maths 2011 Mid Year Exam SolutionsjimmytanlimlongNessuna valutazione finora
- Ath em Ati CS: L.K .SH Arm ADocumento8 pagineAth em Ati CS: L.K .SH Arm APremNessuna valutazione finora
- 3472 MT - Skema Kertas 2Documento10 pagine3472 MT - Skema Kertas 2Yeow Pow Choo100% (1)
- Practicse Test 2 CalcDocumento2 paginePracticse Test 2 CalcPrasanth PillaiNessuna valutazione finora
- C4 January 2006 Mark SchemeDocumento6 pagineC4 January 2006 Mark Schemeshariz500Nessuna valutazione finora
- MA2211 NotesDocumento145 pagineMA2211 NotesBala SubramanianNessuna valutazione finora
- Sajc 2010 Prelim Math p1 SolnDocumento10 pagineSajc 2010 Prelim Math p1 SolnAh XiuNessuna valutazione finora
- RT Solutions-09!10!2011 XIII VXY Paper II Code BDocumento18 pagineRT Solutions-09!10!2011 XIII VXY Paper II Code Bvishal27042233Nessuna valutazione finora
- Ath em Ati CS: L.K .SH Arm ADocumento5 pagineAth em Ati CS: L.K .SH Arm APremNessuna valutazione finora
- Inequation & Equation Solutions FinalDocumento67 pagineInequation & Equation Solutions FinalAkshay PatelNessuna valutazione finora
- 102 2013 1 BDocumento20 pagine102 2013 1 BmatshonaNessuna valutazione finora
- RT Solutions-09!10!2011 XIII VXY Paper II Code ADocumento18 pagineRT Solutions-09!10!2011 XIII VXY Paper II Code Avishal27042233Nessuna valutazione finora
- 2013 - 2014 H2 Maths JJC Promo SolnsDocumento11 pagine2013 - 2014 H2 Maths JJC Promo SolnsLionel Torres LeeNessuna valutazione finora
- 3NA SA1 (AM Solution)Documento8 pagine3NA SA1 (AM Solution)johnlim199Nessuna valutazione finora
- Resenja Zadataka 30.6.2009 inDocumento9 pagineResenja Zadataka 30.6.2009 inVanja MaricNessuna valutazione finora
- Section G: Integer Answer Type: X FX F XDocumento10 pagineSection G: Integer Answer Type: X FX F XsatwiksmNessuna valutazione finora
- c4 Jan 2008 MsDocumento21 paginec4 Jan 2008 MsMk D. AssassinoNessuna valutazione finora
- Answers Are You Ready For CalculusDocumento6 pagineAnswers Are You Ready For CalculusKevin HsiehNessuna valutazione finora
- Mid IDocumento11 pagineMid IpassmefoolNessuna valutazione finora
- Solutions To Home Practice Test-5/Mathematics: Differential Calculus - 2 HWT - 1Documento12 pagineSolutions To Home Practice Test-5/Mathematics: Differential Calculus - 2 HWT - 1varunkohliinNessuna valutazione finora
- PJC h2 Math p1 SolutionsDocumento13 paginePJC h2 Math p1 SolutionsjimmytanlimlongNessuna valutazione finora
- Precalculus Review: For Problems 1 Through 3, Let P (1, 3) and Q (5, - 3)Documento7 paginePrecalculus Review: For Problems 1 Through 3, Let P (1, 3) and Q (5, - 3)shannonhu519Nessuna valutazione finora
- Solutions To Home Practice Test/Mathematics: Integral Calculus-2 HWT - 1Documento12 pagineSolutions To Home Practice Test/Mathematics: Integral Calculus-2 HWT - 1varunkohliinNessuna valutazione finora
- IIT 2012 12 13 p1 p2 Mat UN4 SADocumento66 pagineIIT 2012 12 13 p1 p2 Mat UN4 SAAnkit RaiNessuna valutazione finora
- Rvhs h2 Math p1 SolutionsDocumento13 pagineRvhs h2 Math p1 SolutionsjimmytanlimlongNessuna valutazione finora
- RT Solutions-22!01!2012 XIII VXY Paper I Code A SolDocumento16 pagineRT Solutions-22!01!2012 XIII VXY Paper I Code A Solvishal110085Nessuna valutazione finora
- Eamcet 2014 Engineering Key SolutionsDocumento42 pagineEamcet 2014 Engineering Key Solutionsandhracolleges100% (1)
- 2006 AJC H2 MY SolnDocumento9 pagine2006 AJC H2 MY Solnjunie9201Nessuna valutazione finora
- 2007 YJC Paper 1solDocumento12 pagine2007 YJC Paper 1solYudi KhoNessuna valutazione finora
- Dhs h2 Math p1 SolutionDocumento11 pagineDhs h2 Math p1 SolutionjimmytanlimlongNessuna valutazione finora
- Mathematics Alternative A AnswersDocumento5 pagineMathematics Alternative A Answersmoggadavid480Nessuna valutazione finora
- 2012 ACJC Prelim H2 Math SolnDocumento15 pagine2012 ACJC Prelim H2 Math Solnckhowh_23284524667% (3)
- RT Solutions-Practice Test Papers XIII VXY 1 To 6 SolDocumento40 pagineRT Solutions-Practice Test Papers XIII VXY 1 To 6 Solvishal110085Nessuna valutazione finora
- Penang JitSin MathsT P1 2015 QADocumento13 paginePenang JitSin MathsT P1 2015 QAlingbooNessuna valutazione finora
- HCI H2 Maths 2012 Prelim P1 SolutionsDocumento12 pagineHCI H2 Maths 2012 Prelim P1 Solutionsnej200695Nessuna valutazione finora
- AJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1Documento12 pagineAJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1jimmytanlimlongNessuna valutazione finora
- Misrimal Navajee Munoth Jain Engineering College, Chennai - 97Documento22 pagineMisrimal Navajee Munoth Jain Engineering College, Chennai - 97Vishnu Krishna KumarNessuna valutazione finora
- 2 Overview of Numerical AnalysisDocumento59 pagine2 Overview of Numerical AnalysisVashish RamrechaNessuna valutazione finora
- MJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1Documento22 pagineMJC JC 2 H2 Maths 2011 Mid Year Exam Solutions Paper 1jimmytanlimlongNessuna valutazione finora
- Misrimal Navajee Munoth Jain Engineering College, Chennai - 97Documento26 pagineMisrimal Navajee Munoth Jain Engineering College, Chennai - 97bhagyagr8Nessuna valutazione finora
- MCP-06-02-2011 Paper-1 11th (PQRS & JK) Code ADocumento16 pagineMCP-06-02-2011 Paper-1 11th (PQRS & JK) Code AYash SharmaNessuna valutazione finora
- 2009 SRJC Paper2 SolutionsDocumento24 pagine2009 SRJC Paper2 SolutionsFang Wen LimNessuna valutazione finora
- 2008 h2 Math Prelim p1 (Solns)Documento19 pagine2008 h2 Math Prelim p1 (Solns)Utsav NiroulaNessuna valutazione finora
- 2014 2 SARAWAK SMKStJoseph Kuching MATHS QADocumento11 pagine2014 2 SARAWAK SMKStJoseph Kuching MATHS QASK100% (3)
- Suggested Answer Scheme MAT 565/480 (Advanced Differential Equation) JANUARY 2012Documento4 pagineSuggested Answer Scheme MAT 565/480 (Advanced Differential Equation) JANUARY 2012Fakhrur RaziNessuna valutazione finora
- Student Version Solutions 2 SEMESTER 2 1Documento4 pagineStudent Version Solutions 2 SEMESTER 2 1Lovingmore LavasNessuna valutazione finora
- Edexcel C3 June 2005 To June 2011 All Questions Mark SchemeDocumento44 pagineEdexcel C3 June 2005 To June 2011 All Questions Mark SchemeOrhan AtestemurNessuna valutazione finora
- EE341 FinalDocumento4 pagineEE341 FinalLe HuyNessuna valutazione finora
- 2011 Set B Mock Paper 1 SolutionsDocumento15 pagine2011 Set B Mock Paper 1 SolutionsJordan TiongNessuna valutazione finora
- IIT JEE Maths SolutionsDocumento7 pagineIIT JEE Maths SolutionsVishal GaudNessuna valutazione finora
- Pure Mathematics: For CAPEDocumento11 paginePure Mathematics: For CAPERonaldoNessuna valutazione finora
- Analytic Geometry: Graphic Solutions Using Matlab LanguageDa EverandAnalytic Geometry: Graphic Solutions Using Matlab LanguageNessuna valutazione finora
- Test Bank for Precalculus: Functions & GraphsDa EverandTest Bank for Precalculus: Functions & GraphsValutazione: 5 su 5 stelle5/5 (1)
- Ten-Decimal Tables of the Logarithms of Complex Numbers and for the Transformation from Cartesian to Polar Coordinates: Volume 33 in Mathematical Tables SeriesDa EverandTen-Decimal Tables of the Logarithms of Complex Numbers and for the Transformation from Cartesian to Polar Coordinates: Volume 33 in Mathematical Tables SeriesNessuna valutazione finora
- Trigonometric Ratios to Transformations (Trigonometry) Mathematics E-Book For Public ExamsDa EverandTrigonometric Ratios to Transformations (Trigonometry) Mathematics E-Book For Public ExamsValutazione: 5 su 5 stelle5/5 (1)
- SKHTSKSS 2013-2014 F4 1st Term M1 SolutionDocumento8 pagineSKHTSKSS 2013-2014 F4 1st Term M1 SolutionIam Alvin ChristopherNessuna valutazione finora
- Indices, Surds and LogarithmDocumento13 pagineIndices, Surds and LogarithmTutor World Online86% (22)
- Slides 2022 Week 6Documento165 pagineSlides 2022 Week 6mNessuna valutazione finora
- Quarter 1 - Week 8: Learning Activity Sheet 1 Representing Real-Life Situations Using Logarithmic FunctionsDocumento16 pagineQuarter 1 - Week 8: Learning Activity Sheet 1 Representing Real-Life Situations Using Logarithmic FunctionsJiwon ParkNessuna valutazione finora
- Introduction To Matlab: School of Mathematics and Statistics University of South Australia February, 2005Documento59 pagineIntroduction To Matlab: School of Mathematics and Statistics University of South Australia February, 2005elecbNessuna valutazione finora
- Add Maths Year 9Documento12 pagineAdd Maths Year 9Yenny TigaNessuna valutazione finora
- Calculus II by Paul DawkinsDocumento379 pagineCalculus II by Paul Dawkinsdandalf02100% (1)
- Common Derivatives IntegralsDocumento4 pagineCommon Derivatives IntegralsMayank Raj100% (1)
- Mathematical Methods: PHY250 Physics Core For Level 2Documento48 pagineMathematical Methods: PHY250 Physics Core For Level 2DododNessuna valutazione finora
- Chapter 1: Number SystemDocumento9 pagineChapter 1: Number Systemzan2812Nessuna valutazione finora
- Self-Learning Module For Senior High School LearnersDocumento14 pagineSelf-Learning Module For Senior High School LearnersMykhaela Louize GumbanNessuna valutazione finora
- Symbolic Manipulations Unit 2 KEYDocumento2 pagineSymbolic Manipulations Unit 2 KEYDestiny SumaniNessuna valutazione finora
- L11 Exponential and Logarthmic FunctionsDocumento25 pagineL11 Exponential and Logarthmic FunctionsRamona RodriguezNessuna valutazione finora
- Geomathematics: Lab Manual For Geology 351Documento165 pagineGeomathematics: Lab Manual For Geology 351Anca SesermanNessuna valutazione finora
- 4stt121 Study GuideDocumento109 pagine4stt121 Study Guidenonoandiswa96Nessuna valutazione finora
- Lec 9.1 IntegralsDocumento30 pagineLec 9.1 Integralserlangga1017Nessuna valutazione finora
- AAMS1613 Chapter 1 NumberDocumento12 pagineAAMS1613 Chapter 1 Number木木聪Nessuna valutazione finora
- Essential MATLAB For Engineers and Scientists (YTU, IT Group)Documento520 pagineEssential MATLAB For Engineers and Scientists (YTU, IT Group)Hein Htet Ko100% (2)
- Additional Derivative Topics: Section 1 The Constant e and Continuous Compound InterestDocumento48 pagineAdditional Derivative Topics: Section 1 The Constant e and Continuous Compound InterestArun GhatanNessuna valutazione finora
- Algebra 2 and 3-Take Home ProblemsDocumento8 pagineAlgebra 2 and 3-Take Home ProblemsYden C SilvestreNessuna valutazione finora
- 3 - 3 - 4 Properties of Logs PDFDocumento24 pagine3 - 3 - 4 Properties of Logs PDFLazar MihaiNessuna valutazione finora
- 1.6 Inverse Trigonometric and Inverse Hyperbolic Functions of Complex NumbersDocumento5 pagine1.6 Inverse Trigonometric and Inverse Hyperbolic Functions of Complex NumbersTyrone PaulinoNessuna valutazione finora
- Malek - The Kinetic Analysis of Non-Isothermal Data, 1992Documento13 pagineMalek - The Kinetic Analysis of Non-Isothermal Data, 1992oreamigNessuna valutazione finora
- Gmath Continuation Module 1Documento30 pagineGmath Continuation Module 1あい アリソンNessuna valutazione finora
- 2.03.asymptotic AnalysisDocumento55 pagine2.03.asymptotic AnalysisRubab AnamNessuna valutazione finora
- MAC1105 College Algebra All Formulas List Academic SystemsDocumento5 pagineMAC1105 College Algebra All Formulas List Academic SystemsYadwinder SinghNessuna valutazione finora
- Log LinearizationDocumento18 pagineLog LinearizationZuzana MacovaNessuna valutazione finora
- Elementary Calculus With Applications (Elena Devdariani)Documento135 pagineElementary Calculus With Applications (Elena Devdariani)Omar “XlordBayder” BaderNessuna valutazione finora
- Indeterminate FormsDocumento6 pagineIndeterminate FormsGabriel Dave AlamoNessuna valutazione finora
- API 111 Solutions 2Documento12 pagineAPI 111 Solutions 2Anonymous L7XrxpeI1zNessuna valutazione finora