A tensile structure is a construction of elements carrying only tension and

no compression or bending. The term tensile should not be confused with tensegrity,
which is a structural form with both tension and compression elements.
Most tensile structures are supported by some form of compression or bending
elements, such as masts (as in The O
2
, formerly the Millennium Dome), compression
rings or beams.
Tensile membrane structures are most often used as roofs as they can economically
and attractively span large distances.
This form of construction has only become
more rigorously analyzed and widespread in large structures in the latter part of the
twentieth century. Tensile structures have long been used intents, where the guy
ropes provide pre-tension to the fabric and allow it to withstand loads.
Russian engineer Vladimir Shukhov was one of the first to develop practical
calculations of stresses and deformations of tensile structures, shells and
membranes. Shukhov designed eight tensile structures and thin-shell
structures exhibition pavilions for the Nizhny Novgorod Fair of 1896, covering the
area of 27,000 square meters. A more recent large-scale use of a membrane-
covered tensile structure is the Sidney Myer Music Bowl, constructed in 1958.
Antonio Gaudi used the concept in reverse to create a compression-only structure
for the Colonia Guell Church. He created a hanging tensile model of the church to
calculate the compression forces and to experimentally determine the column and
vault geometries.
The concept was later championed by German architect and engineer Frei Otto,
whose first use of the idea was in the construction of the German pavilion at Expo
67 in Montreal. Otto next used the idea for the roof of the Olympic Stadium for
the 1972 Summer Olympics in Munich.
Since the 1960s, tensile structures have been promoted
by designers and engineers such as Ove Arup, Buro Happold, Walter Bird of Birdair,
Inc., Frei Otto, Eero Saarinen, Horst Berger,Matthew Nowicki, Jorg Schlaich, the duo
of Nicholas Goldsmith & Todd Dalland at FTL Design & Engineering
Studio and David Geiger.
Steady technological progress has increased the popularity of fabric-roofed
structures. The low weight of the materials makes construction easier and cheaper
than standard designs, especially when vast open spaces have to be covered.
The horizontal and vertical reactions :


By geometry:
The length of the cable:

The tension in the cable:

By substitution:

The tension is also equal to:
T = wR
The extension of the cable upon being loaded is (from Hooke's
Law, where the axial stiffness, k, is equal to ):

where E is the Young's modulus of the cable and A is its
cross-sectional area.
If an initial pretension, T
0
is added to the cable, the
extension becomes:

Combining the above equations gives:

By plotting the left hand side of this equation
against T, and plotting the right hand side on the
same axes, also against T, the intersection will give
the actual equilibrium tension in the cable for a
given loading w and a given pretension T
0
.
[edit]Cable with central point load


A similar solution to that above can be derived
where:
By equilibrium:


By geometry:

This gives the following relationship:

As before, plotting the left hand side and right hand side of the equation against the
tension, T, will give the equilibrium tension for a given pretension, T
0
and load, W.
Tensioned cable oscillations
The fundamental natural frequency, f
1
of tensioned cables is given by:
where: T = tension in newtons, m = mass in kilograms and L =
span length.



Torsion Theory



Shear Strain: c
s
= r u / L
Shear Stress: o
s
= T r /J
Angle of Twist: u = TL/(JG)
c
s
= Shear strain (radians)
o
s
= Shear Stress (MPa)
u= Angle of twist (radians)
L = Gauge length (mm)
r = Radius (mm)
G = Shear Modulus (MPa)
T = Torque (Nm)
J = Polar Moment of Inertia (mm
4
)

Where J is the Polar Second Moment of Area, which is used when under
torsion. For a cylinder...



For a pipe, calculate J for the outside diameter, then SUBTRACT the J for
the inside diameter (the hole).
We do not have torsion equations for square shapes - these equations only work for circular
shapes (round rods and pipes). Anything else will deform under torsion and will not obey
these formulas. Open shapes like a slit pipe can be almost as strong in bending as a closed
pipe, but hundreds of times weaker in torsion.







General Background
If a beam is supported at two points, and a load is applied anywhere on the beam,
deformation will occur. When these loads are applied either longitudinally outside or inside
of the supports, this elastic bending can be mathematically predicted based on material
properties and geometry.
Determination of Curvature
Curvature at any point on the beam is calculated from the moment of loading (M), the
stiffness of the material (E), and the first moment of inertia (I.) The following expression
defines the curvature in these parameters as 1/, where is the radius of curvature.
I E
M

1

Equation 1
Equation 1 does not account for shearing stresses.
Curvature can also be found using calculus. Defining y as the deflection and x as the position
along the longitudinal axis, the expression becomes
2
3
2
2
2
1
1
(
(

|
.
|

\
|
+
=
dx
dy
dx
y d

Equation 2
Central Loading
Central loading on a beam can be thought of as a simple beam with two supports as shown
below.

Figure 1
Applying equilibrium to the free body equivalent of Figure 1, several expressions can be
derived to mathematically explain central loading.
2
0
2 2
0
0
P
R R P R F
P
R L R
L P
M
R F
ay c ay y
C C A
ax x
= + = = | +
= + = =
= = +

Equation 3, 4, and 5
Figure 2 and 3 act as free body diagrams for the section between AB and BC respectively.

Figure 2

Figure 3
Solving the reactions between AB and BC, equation 1 can be expressed as
L x
L L P x P
dx
y d
I E
L
x
x P
dx
y d
I E
s s + =
s s =
2 2 2
2
0
2
2
2
2
2

Equation 6, 7
Integrating twice, Equation 6 becomes
L x
L
C x C
x L P x P
y I E
L
x C x C
x P
y I E
s s + + + =
s s + + =
2 4 12
2
0
12
4 3
2 3
2 1
3

Equation 8, 9
To determine the constants, conditions at certain positions on the beam can be applied.
Knowing the deflection at each of the supports, as well as the slope at the top of the curve is
zero, the constants can be derived to
48 16
3
0
16
3
4
2
3 2
2
1
L P
C L P C C
L P
C = = = =
Equation 10, 11, 12, and 13
Combining Equations 8 and 9 with 10 through 13, the expressions for deflection can be
expressed as
L x
L L P x L P x L P x P
y I E
L
x
x L P x P
y I E
s s + + =
s s =
2 48 16
3
4 12
2
0
16 12
3 2 2 3
2 3

Equation 14, 15
Overhanging Loads
Overhanging loading on a beam is similar to that of central loading. In overhanging loading,
a simple beam is supported with two supports and two loads as shown below.

Figure 4
Using similar methods used previously for central loading, the equation for determination of
deflection as a function of position, load, length, stiffness, and geometry can be derived as
( ) ( ) L x x b a
L P x a P
b a
L
x P
y I E s s + + = 0 2
6 2 6
2 3

Equation 16






DIRECT SHEAR TEST
Purpose:
This test is performed to determine the consolidated-drained shear strength
of a sandy to silty soil. The shear strength is one of the most important engineering
properties of a soil, because it is required whenever a structure is dependent on the
Analysis:


1) Calculate the density of the soil sample from the mass of soil and volume of the shear
box.

2) Convert the dial readings to the appropriate length and load units and enter
the values on the data sheet in the correct locations. Compute the sample area A, and the
vertical (Normal) stress, sv.

sv=Nv /A

Where: Nv = normal vertical force, and sv = normal vertical stress

3) Calculate shear stress (t) using t =Fh/A

Where Fh= shear stress (measured with shear load gage)

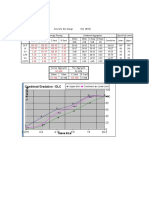
4) Plot the horizontal shear stress (t) versus horizontal (lateral) displacement
?H.

(5) Calculate the maximum shear stress for each test.

6) Plot the value of the maximum shear stress versus the corresponding
vertical stress for each test, and determine the angle of internal friction (f)
from the slope of the approximated Mohr-Coulomb failure envelope.





















POLITEKNIK SULTAN AZLAN SHAH
NAMA : MOHAMAD ZULHIFNI BIN MOHD FAUZI 15DKM10F1080
MUHAMMAD ARIFF BIN AB WAHAB 15DKM10F1062

NAMA PENSYARAH : EN AMIRUDDIN