Documenti di Didattica
Documenti di Professioni
Documenti di Cultura
Examples On Sampling and Aliasing Phenomena: Example 1
Caricato da
Hiren MewadaDescrizione originale:
Titolo originale
Copyright
Formati disponibili
Condividi questo documento
Condividi o incorpora il documento
Hai trovato utile questo documento?
Questo contenuto è inappropriato?
Segnala questo documentoCopyright:
Formati disponibili
Examples On Sampling and Aliasing Phenomena: Example 1
Caricato da
Hiren MewadaCopyright:
Formati disponibili
MEEN 364 Lecture 4
Parasuram April 2, 2003
EXAMPLES ON SAMPLING AND ALIASING PHENOMENA
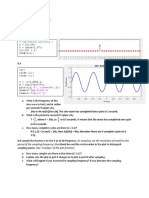
Example 1: Consider the following two analog signals
x1 (t ) = cos 2 (10)t , x 2 (t ) = cos 2 (50)t ,
which are sampled at a rate of Fs = 40 Hz. The corresponding discrete time signals are
x1 (n) = cos 2 (
10 )n = cos n, 40 2 50 5 x 2 (n) = cos 2 ( )n = cos n. 2 40
However, cos
n 5 n = cos(2 n + ) = cos n. 2 2 2
Hence x1 (n) = x 2 (n) . Thus the signals are identical and consequently indistinguishable. If we are given the sampled values generated by cos
n , there is some ambiguity as to 2 whether these sampled values correspond to x1(t) or x2(t). Since x2(t) yields exactly the same values as x1(t) when the two are sampled at Fs = 40 samples per second, we say that the frequency F2 = 50 Hz is an alias of the frequency F1 = 10 Hz at the sampling rate of 40 samples per second.
Example 2:
Consider the analog signal
x a (t ) = 3 cos100 t. a) Determine the minimum sampling rate required to avoid aliasing. b) Suppose that the signal is sampled at the rate of Fs = 200 Hz, what is the discretetime signal obtained after sampling? c) Suppose that the signal is sampled at the rate of Fs = 75 Hz, what is the discretetime signal obtained after sampling? d) What is the frequency of a sinusoid that yields samples identical to those obtained in part (c)?
MEEN 364 Lecture 4 a) The frequency of the analog signal can be calculated as 2 F1 = 100 , F1 = 50. Hence the minimum sampling rate required to avoid aliasing is Fs = 100 Hz. b) If the signal is sampled at Fs = 200 Hz, then the discrete-time signal is
Parasuram April 2, 2003
100 x(n) = 3 cos( )n = 3 cos( )n. 200 2
c) If the signal is sampled at Fs = 75 Hz, then the discrete-time signal is 100 4 x(n) = 3 cos( )n = 3 cos( )n 75 3 2 = 3 cos(2 )n 3 2 = 3 cos( )n. 3 d) For the sampling rate of Fs = 75 Hz, we have F2 = fFs = 75 f 1 The frequency of the sinusoid in part (c) is f = . Hence 3 75 F2 = 75 f = = 25. 3 Clearly, the sinusoidal signal
y (t ) = 3 cos 2 F2 t = 3 cos 50 t
sampled at Fs = 75 samples per second yields identical samples. Hence F1 = 50 Hz is an alias of F2 = 25 Hz for the sampling rate Fs = 75 Hz.
MEEN 364 Lecture 4
Example 3:
Parasuram April 2, 2003
Consider the analog signal x a (t ) = 3 cos 50 t + 10 sin 300 t cos100 t. What is the Nyquist rate for this signal? The frequencies present in the signal above are F1 = 25, F2 = 150, F3 = 50. Thus Fmax = 150 Hz and according to the sampling theorem Fs > 2 Fmax = 300 Hz . The Nyquist rate is FN = 2Fmax. Hence FN = 300 Hz.
Discussion
It should be observed that the signal component 10 sin 300 t , sampled at the Nyquist rate FN = 300 Hz, results in samples 10 sin n , which are identically zero. In other words, we are sampling the analog signal at its zero-crossing points, and hence we miss the signal component completely. This situation would not occur if the sinusoid is offset in phase by some amount . In such a case we have 10 sin(300 t + ) sampled at the Nyquist rate FN = 300 samples per second, which yields the samples 10 sin( n + ) = 10(sin n cos + cos n sin )
= 10 sin cos n = (1) n 10 sin .
Thus if 0 or , the samples of the sinusoid taken at Nyquist rate are not all zero. However, we still cannot obtain the correct amplitude from the samples when the phase is unknown. A simple remedy that avoids this potentially troublesome situation is to sample the analog signal at a rate higher than the Nyquist rate.
MEEN 364 Lecture 4
Example 4:
Parasuram April 2, 2003
Consider the analog signal x a (t ) = 3 cos 2000 t + 5 sin 6000 t + 10 cos12000 t. a) What is the Nyquist rate for this signal? b) Suppose that the signal is sampled at the rate of Fs = 5000 samples per second, what is the discrete-time signal obtained after sampling? c) What is the analog signal we can reconstruct from the samples? a) The frequencies existing in the above signal are
F1 = 1000 Hz, F2 = 3000 Hz, F3 = 6000 Hz. Thus Fmax = 6000 Hz and according to the sampling theorem, Fs > 2 Fmax = 12000 Hz . The Nyquist rate is FN = 2Fmax = 12000 Hz. b) The discrete-time signal of the signal sampled at 5000 samples per second is
2000 6000 12000 )n + 5 sin( )n + 10 cos( )n 5000 5000 5000 1 3 6 = 3 cos 2 ( )n + 5 sin 2 ( )n + 10 cos 2 ( )n 5 5 5 1 2 1 = 3 cos 2 ( )n + 5 sin 2 (1 )n + 10 cos 2 (1 + )n 5 5 5 1 2 1 = 3 cos 2 ( )n + 5 sin 2 ( )n + 10 cos 2 ( )n 5 5 5 x(n) = 3 cos(
Finally, we obtain 1 2 x(n) = 13 cos 2 ( )n 5 sin 2 ( )n . 5 5 Since Fs = 5000 Hz, the folding frequency is Fs/2 = 2500 Hz. This is the maximum frequency that can be represented uniquely by the sampled signal.
MEEN 364 Lecture 4
Parasuram April 2, 2003
c) Since only the frequency components at 1000 Hz and 2000 Hz are present in the sampled signal, the analog signal that can be recovered is y (t ) = 13 cos 2 (1000)t 5 sin 2 (2000)t which is obviously different from the original signal x(t). This distortion of the original analog signal was caused by the aliasing effect, due to the low sampling rate used.
Assignment
1) Consider the analog signal x(t ) = 3 cos 600 t + 2 cos1800 t . a) Determine the minimum sampling rate required to avoid aliasing. b) What is the Nyquist rate for the signal x(t)? c) Suppose that the signal is sampled at Fs = 2000 Hz, what is the discrete-time signal obtained after the sampling? What are the frequencies in the resulting discrete-time signal? d) If the sampling rate is Fs = 600 Hz, then what is the maximum frequency that can be recovered from the discrete-time signal? 2) An analog signal contains frequencies up to 10 kHz. a) What range of sampling frequencies allows exact reconstruction of the signal from its samples? b) What is the Nyquist rate for the signal? c) If the sampling rate Fs is chosen as 10 kHz, then what is the maximum frequency that can be represented uniquely by the sampled signal?
Potrebbero piacerti anche
- Hyrdoacoustic Ocean Exploration: Theories and Experimental ApplicationDa EverandHyrdoacoustic Ocean Exploration: Theories and Experimental ApplicationNessuna valutazione finora
- Interactions between Electromagnetic Fields and Matter: Vieweg Tracts in Pure and Applied PhysicsDa EverandInteractions between Electromagnetic Fields and Matter: Vieweg Tracts in Pure and Applied PhysicsNessuna valutazione finora
- Signals and SystemsDocumento3 pagineSignals and SystemsJefrilAmboyNessuna valutazione finora
- Lab 4 MatlabDocumento3 pagineLab 4 MatlabArif AmiruddinNessuna valutazione finora
- Matlab Assignment-02 SEM-II-2016-2017 PDFDocumento6 pagineMatlab Assignment-02 SEM-II-2016-2017 PDFfarhanfendiNessuna valutazione finora
- DSM2 1102 Week 2Documento4 pagineDSM2 1102 Week 2Hugo LeiteNessuna valutazione finora
- Sampling Theorem and Pulse ModulationDocumento27 pagineSampling Theorem and Pulse ModulationPavan PrakashNessuna valutazione finora
- Pulse Amplitude ModulationDocumento86 paginePulse Amplitude ModulationPraful Jagtap100% (1)
- Slide-5 Discrete Fourier Transfor-1Documento36 pagineSlide-5 Discrete Fourier Transfor-1musaNessuna valutazione finora
- Ch03Sampling and AliasDocumento8 pagineCh03Sampling and AliasImran MehmoodNessuna valutazione finora
- Lab I12Documento8 pagineLab I12Lulzim LumiNessuna valutazione finora
- Sampling and ReconstructionDocumento40 pagineSampling and ReconstructionHuynh BachNessuna valutazione finora
- 183 EEE311Lesson2 PDFDocumento35 pagine183 EEE311Lesson2 PDFMasud SarkerNessuna valutazione finora
- ECE411 - Problem Set 1 - IntroductionDocumento7 pagineECE411 - Problem Set 1 - IntroductionMartine JimenezNessuna valutazione finora
- Continous Time Signal Vs Discrete Time SignalDocumento9 pagineContinous Time Signal Vs Discrete Time SignalFairoz UsuNessuna valutazione finora
- Digital Signal Processing - 1Documento77 pagineDigital Signal Processing - 1Sakib_SL100% (1)
- 6.1 Sampling and Reconstruction of Analog Signals: Piyush Kumar 20104148901 G.E.C, KaimurDocumento9 pagine6.1 Sampling and Reconstruction of Analog Signals: Piyush Kumar 20104148901 G.E.C, KaimurEr VishuuuNessuna valutazione finora
- Lecture #5, Fall 2003: ECE 6602 Digital CommunicationsDocumento12 pagineLecture #5, Fall 2003: ECE 6602 Digital Communicationsshakr123Nessuna valutazione finora
- DSP Assignments 1 Solution Spring 2020 PDFDocumento3 pagineDSP Assignments 1 Solution Spring 2020 PDFruss90Nessuna valutazione finora
- DSP-Chapter1 Student 28062015Documento45 pagineDSP-Chapter1 Student 28062015NguyenThaoNessuna valutazione finora
- Examples Fourier - PsDocumento3 pagineExamples Fourier - PsAntonio MartinezNessuna valutazione finora
- Digital Signal Processing: b, where (a, b) can be (t t x πDocumento5 pagineDigital Signal Processing: b, where (a, b) can be (t t x πSugan MohanNessuna valutazione finora
- DSP Unit-I Part 2 Updated 20.7.2020Documento57 pagineDSP Unit-I Part 2 Updated 20.7.2020sivaNessuna valutazione finora
- DSP Assignment 1 AshwinDocumento6 pagineDSP Assignment 1 AshwinAkshaySudhirNessuna valutazione finora
- Fall Semester 2019-20 ECE4001 Digital Communication Systems Digital Assignment 1 Due Date: 09/09/2019Documento4 pagineFall Semester 2019-20 ECE4001 Digital Communication Systems Digital Assignment 1 Due Date: 09/09/2019Grace ARORANessuna valutazione finora
- Fall Semester 2019-20 ECE4001 Digital Communication Systems Digital Assignment 1 Due Date: 09/09/2019Documento4 pagineFall Semester 2019-20 ECE4001 Digital Communication Systems Digital Assignment 1 Due Date: 09/09/2019PRANAV KUMAR 17BEC0473Nessuna valutazione finora
- Signals and Systems (Practice Questions - Sampling)Documento8 pagineSignals and Systems (Practice Questions - Sampling)madivala nagarajaNessuna valutazione finora
- Fourier MathcadDocumento11 pagineFourier MathcadAlberto OlveraNessuna valutazione finora
- FM ExercisesDocumento5 pagineFM ExercisesanililhanNessuna valutazione finora
- Fourier Transform 3Documento8 pagineFourier Transform 3May Thet TunNessuna valutazione finora
- Comm AssntIIDocumento6 pagineComm AssntIIkalNessuna valutazione finora
- Sampling 1Documento1 paginaSampling 1Debdutta ChatterjeeNessuna valutazione finora
- Digital Signal Processing: Lecture 3 - 4Documento35 pagineDigital Signal Processing: Lecture 3 - 4ekmemonNessuna valutazione finora
- Assignment1 SolutionDocumento6 pagineAssignment1 SolutionninjaministerNessuna valutazione finora
- CTFT DTFT DFTDocumento6 pagineCTFT DTFT DFTZülal İlayda ÖzcanNessuna valutazione finora
- Act 4 DSPDocumento15 pagineAct 4 DSPChristian GomezNessuna valutazione finora
- ME 360, Fall 2021 Problem Set 5 Due at 3PM Monday, Oct 4Documento2 pagineME 360, Fall 2021 Problem Set 5 Due at 3PM Monday, Oct 4Rounak ChowdhuryNessuna valutazione finora
- DSP-1 (Intro) (S)Documento77 pagineDSP-1 (Intro) (S)karthik0433Nessuna valutazione finora
- Laboratory Activity 2Documento3 pagineLaboratory Activity 2Rey navaNessuna valutazione finora
- CH 17Documento8 pagineCH 17Arthur Traferi NassifNessuna valutazione finora
- Problemas Parte I Comunicaciones DigitalesDocumento17 pagineProblemas Parte I Comunicaciones DigitalesNano GomeshNessuna valutazione finora
- ECE515FL - Activity4 (Audio Synthesis)Documento7 pagineECE515FL - Activity4 (Audio Synthesis)Mikhail OdulioNessuna valutazione finora
- TP TDS 2 PDFDocumento8 pagineTP TDS 2 PDFLam NovoxNessuna valutazione finora
- Lab 1Documento3 pagineLab 1sunshine heavenNessuna valutazione finora
- Unit-1 EeeDocumento65 pagineUnit-1 EeeVinoth MuruganNessuna valutazione finora
- 4 Audio SynthesisDocumento10 pagine4 Audio SynthesisCaye LalimarmoNessuna valutazione finora
- Lab 02Documento8 pagineLab 02Joevane B. EscrupoloNessuna valutazione finora
- Solution Assignment1 B PDFDocumento5 pagineSolution Assignment1 B PDFTanzeel AhmadNessuna valutazione finora
- 16EC30021 - DSP Lab Report - Exp01 - PalakDocumento8 pagine16EC30021 - DSP Lab Report - Exp01 - PalakARUOS SouraNessuna valutazione finora
- Digital Communication 601 - TutorialDocumento12 pagineDigital Communication 601 - TutorialHemanth Vinay Kumar0% (1)
- Extra Exercise Solutions Chapter 5Documento9 pagineExtra Exercise Solutions Chapter 5Vikri JanuarismaNessuna valutazione finora
- 108 Module 1 QuizDocumento8 pagine108 Module 1 QuizVivien VilladelreyNessuna valutazione finora
- Real Analysis and Probability: Solutions to ProblemsDa EverandReal Analysis and Probability: Solutions to ProblemsNessuna valutazione finora
- Seminar on Micro-Local Analysis. (AM-93), Volume 93Da EverandSeminar on Micro-Local Analysis. (AM-93), Volume 93Nessuna valutazione finora
- Mathematical Tables: Tables of in G [z] for Complex ArgumentDa EverandMathematical Tables: Tables of in G [z] for Complex ArgumentNessuna valutazione finora
- Resonance Enhancement in Laser-Produced Plasmas: Concepts and ApplicationsDa EverandResonance Enhancement in Laser-Produced Plasmas: Concepts and ApplicationsNessuna valutazione finora
- Fundamentals of Electronics 3: Discrete-time Signals and Systems, and Quantized Level SystemsDa EverandFundamentals of Electronics 3: Discrete-time Signals and Systems, and Quantized Level SystemsNessuna valutazione finora
- Dac InterfacingDocumento5 pagineDac InterfacingHiren MewadaNessuna valutazione finora
- Digital Communications by J.S.chitodeDocumento186 pagineDigital Communications by J.S.chitodeBabulal Meena83% (52)
- Dcomm - Lesson Plan2011Documento3 pagineDcomm - Lesson Plan2011Hiren MewadaNessuna valutazione finora
- PHD Stavros TsantisDocumento196 paginePHD Stavros TsantisHiren MewadaNessuna valutazione finora
- Digital CommunicationDocumento3 pagineDigital CommunicationHiren Mewada50% (2)
- Camara Icantek iCanView232Documento56 pagineCamara Icantek iCanView232TecnoSmartNessuna valutazione finora
- Oraciones RaulDocumento8 pagineOraciones Raul7 Becerril Alcalá AnethNessuna valutazione finora
- HiFi Diamond8 ManualDocumento6 pagineHiFi Diamond8 ManualRonnie AnthonyNessuna valutazione finora
- Uxa2 190CBDocumento3 pagineUxa2 190CBpkb68Nessuna valutazione finora
- Digital Printmaking: Pixels, Dots, and Ink JetsDocumento9 pagineDigital Printmaking: Pixels, Dots, and Ink JetssoujanaNessuna valutazione finora
- AssetDocumento13 pagineAssetrageendrathasNessuna valutazione finora
- Troubleshooting: 5.1 Troubleshooting For Circuit-Breaker Proper (MCCB/ELCB)Documento6 pagineTroubleshooting: 5.1 Troubleshooting For Circuit-Breaker Proper (MCCB/ELCB)ARUNPRASADEEENessuna valutazione finora
- Recorder DuetsDocumento11 pagineRecorder DuetsPedro Daniel Macalupú Cumpén92% (13)
- Philippine Folk Dance PPT 2020 2021Documento28 paginePhilippine Folk Dance PPT 2020 2021Russelle Jay Coronel88% (8)
- Link Budget Calculation: Training Materials For Wireless TrainersDocumento28 pagineLink Budget Calculation: Training Materials For Wireless TrainersusmanNessuna valutazione finora
- Ang ProbinsyanoDocumento35 pagineAng ProbinsyanoJomari MoralesNessuna valutazione finora
- Sithata Ahara - Ven - Ajan Chah TheroDocumento214 pagineSithata Ahara - Ven - Ajan Chah Therowon9100% (1)
- Marketing Strategy of Consumer Durable CompaniesDocumento84 pagineMarketing Strategy of Consumer Durable CompaniesseemranNessuna valutazione finora
- Viva La Vida 3 Violines + Instrumento SoloDocumento16 pagineViva La Vida 3 Violines + Instrumento Soloyayramone100% (1)
- Isabelle VengerovaDocumento70 pagineIsabelle VengerovaPailo76100% (1)
- Music: Quarter 4 - Module 4: Traditional Asian Theater MusicDocumento15 pagineMusic: Quarter 4 - Module 4: Traditional Asian Theater MusicAlexes Alyza CañeteNessuna valutazione finora
- Duet in C Minor Flex Score and PartsDocumento88 pagineDuet in C Minor Flex Score and PartssuperheropmgNessuna valutazione finora
- Qut EN50 27746 Dom Cms UnitDocumento3 pagineQut EN50 27746 Dom Cms UnitSuman SahaNessuna valutazione finora
- Ruimas Basnikas - Company of Minor UtterancesDocumento187 pagineRuimas Basnikas - Company of Minor UtterancesEnough RecordsNessuna valutazione finora
- MTR 2000Documento2 pagineMTR 2000Manrique VasquezNessuna valutazione finora
- Cognitive Radio-Syllabus-1-2-17Documento3 pagineCognitive Radio-Syllabus-1-2-17Pavithra Arul100% (1)
- Show Must Go On LetraDocumento1 paginaShow Must Go On LetraManuel Nazario Guerrero PérezNessuna valutazione finora
- Vega Star Silver - E ManualDocumento2 pagineVega Star Silver - E ManualFredy Ezequiel Benitez RebollarNessuna valutazione finora
- Helix Traveling Wave TubeDocumento18 pagineHelix Traveling Wave Tubeamvarman100% (1)
- Digital Booklet - The Lego® Movie (Original Motion Picture Soundtrack)Documento7 pagineDigital Booklet - The Lego® Movie (Original Motion Picture Soundtrack)Derrick ClementsNessuna valutazione finora
- Physical Education and Health Grade 12: Three Components of FitnessDocumento5 paginePhysical Education and Health Grade 12: Three Components of FitnessAndrew Arciosa Calso100% (2)
- New Microsoft Office Word DocumentDocumento12 pagineNew Microsoft Office Word Documentgadde bharatNessuna valutazione finora
- L Rules Omaha Beach v2Documento34 pagineL Rules Omaha Beach v2cromnNessuna valutazione finora
- IRD-2900 Series: Professional Integrated Receiver DecodersDocumento235 pagineIRD-2900 Series: Professional Integrated Receiver DecodersalbertoJunior2011Nessuna valutazione finora
- Nte996 CA3080 EQUIVALENTEDocumento3 pagineNte996 CA3080 EQUIVALENTERobert GabrielNessuna valutazione finora






















































![Mathematical Tables: Tables of in G [z] for Complex Argument](https://imgv2-2-f.scribdassets.com/img/word_document/282615796/149x198/febb728e8d/1714993295?v=1)






































