INTRODUCTION TO NONLINEAR MECHANICS OF STRUCTURAL ELEMENTS

1. Scope

We shall be concerned with beams and columns. These are structural elements that their
length L is much larger than their other dimensions. We shall examine the behavior of beams
and columns made of different linear and nonlinear materials. Both homogeneous and composite
beams will be examined. Of special interest are the relations of axial force versus axial
deformation, and of bending moment versus curvature.

2. Assumptions for the Analysis

Many assumptions will be made for the analysis of beams and columns. The most important
assumption is the following:
Plane sections before deformation remain plane after deformation.
Note from Figure 1, that plane sections A, B, C, and D in the undeformed beam, remain
plane, even though they are now inclined, in the deformed beam in the locations A’, B’, C’,
and D’ respectively. We shall always assume this to be
true for linear and nonlinear materials, for
homogeneous as well as composite structures. The
assumption is quite realistic as long as the length of
the structure is its predominant dimension. It is
usually required that L $10d, however, sometimes the
assumption is accepted even for cases where L is as
low as 5d with the understanding that the
Figure 1 assumptions is only approximately satisfied. The most
important implication of this assumption is
demonstrated in Figure 2. Since a plane
section before deformation remains
plane after deformation (even though it
has moved and rotated from its original
position), the strains along the depth d
of the section are always linear. This will
be something that we will be going back
to through out the course of this class:
No matter what is the material of the
beam or column plane the strain variation
along the depth of the cross section will
be linear as long as the length is truly
the dominant dimension.
Figure 2

Page 1 January 14, 2010

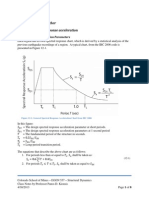
3. Implications of Linear strains on cross-section

Curvature relates to strains

The curvature of a beam at a point (i.e. at a cross-section) is equal to the second derivative of
deflection. Recall from the Mechanics of Materials class the elastic relation:
M = EI y” or M = EI κ, where κ = y” is the curvature. Note that the elastic relation M = EI κ
indicates that under elastic conditions the relation of Moment and curvature is linear with a
slope of EI. It is not difficult to prove that for linear distribution of strain along the cross-
section depth, the curvature is equal to the slope of the strain diagram, that is: κ = εo /c (See
Figure 2).

Elastic Example

Consider the rectangular cross-section of Figure 3 that carries a moment M = 2000 in-k. Let
the material be elastic with modulus of elasticity E = 4000 ksi.

1
F1 = fc b
2 1

1
F2 = f (h - c) b
2 2

Figure 3

Because of the moment, strains will be developed in the cross-section that are compressive on
the top and tensile at the bottom. The strains vary only along the depth of this cross-section,
and are constant across the width. Let the strain at the top fiber be ε1 and the strain at the
bottom fiber be ε2. At a distance c from the top fiber the strains are zero. This is the location
of the neutral axis. The axial stresses and strains are related linearly through the modulus of
elasticity, thus the stresses at the top and bottom fiber are f1 = 4000 ε1 and f2 = 4000 ε2
respectively. Since the strain distribution is linear and f = E ε, the stress distribution is also
linear. Note that f1 and f2 are related through c as follows:
f2 = f1 (h-c)/c (*)
The compressive triangle of stresses generates a force F1 = (½)f1 c b. Similarly, the tensile
triangle generates a force F2 = (½)f2 (h-c) b. The point of application of these forces is at the
centroid of the triangles, i.e. at (2/3) c and (2/3) (h-c) respectively.

The cross-section carries a moment of 2000 in-k and no axial force. This means that the
internal forces must have a resultant of zero or F1=F2.

Page 2 January 14, 2010

From this equilibrium we can calculate c:
(½)f1 c b = (½)f2 (h-c) b or f1 c = f2 (h-c).
If we substitute f2 from (*) we have:
f1 c = f1 (h-c)2/c
From this, we find that c2 = (h-c)2 or c = h-c or c = h/2.
Equation (*) now yields f2 = f1

Note that F1 = F2 = F = (½)f1 (h/2) b = (½) A f1 A 10 A 12 = 60 A f1. These forces form a couple with
moment are d = (4/3) A (h/2) = (2/3) A h = 40/3 in. The moment value of this couple is equal to he
externally applied moment of 2000 in-k. Thus:
2000 = (60 A f1) (40/3) = 800 A f1 or f1 = 2.5 ksi
Of course, this approach as general as it is, it is also unnecessary for an elastic problem since
we can use the simpler expression f1 = (M/I) y or (2000/(12x203/12)x10 = 2.5 ksi.
Now we can find the strains at the top and bottom fiber of the beam: ε1 = f1/E = 2.5/4000 =
0.000625. Of course, ε2 = 0.000625. We can now calculate the corresponding curvature κ = ε1/c
= 0.000625/10 = 0.0000625 in1. Again, for the elastic problem this process is not necessary
since we know that M = EI κ, thus κ = 2000/(4000 x 12 x 203/12) = 0.0000625.

However, for problems that the elastic relation f = Eε is not valid for the entire range of
strains, the expression f = (M/I) y is not valid, and the approach of internal force equilibrium
that was present here is the only means of calculating internal stress distributions.

Inelastic Example

Consider next, a material with response as shown in Figure 4. The material has symmetric
response in tension and compression, but its elastic range is limited. Let fy = 3 ksi and E = 4000
ksi. Thus εy = fy/E = 0.00075. Consider now the same cross-
section as in the previous example subjected to a moment M.
(Figure 5). As the value of M increases the strains along the
depth of the cross-section increase. We’ll start with the
following simple realization: As long as the stress-strain
diagram is symmetric in tension and in compression, and the
cross-section is symmetric about the bending axis, then the
neutral axial due to bending alone will always be at the
Figure 4 centroid of the cross-section. These are the stages of
interest:
1. If M is less the a certain value My then the all strains are smaller than the yield and thus
the stresses are linear (Figure 5b). If the largest strain is equal to εy, then the largest
stress is equal to fy. The tensile and compressive forces are equal and of magnitude
F = ½ fy c b = ½ x 3 x 10 x 12 = 180 kips. Forces F are located at a distance (2/3)c from
the centroid. Thus, the moment that they produce is:
My = 2 x F x (2/3)c = 2 x 180 x 2/3 x 10 = 2400 in-k.

Page 3 January 14, 2010

 The corresponding curvature is κy = εy/c = 0.00075/10 = 0.000075 in-1.

Figure 5
2. Let M > My. Then the strains at the bottom and top fibers are ε > εy. (Figure 5c). For
example, let ε = 0.001. At an inner location x the strain is equal to εy. For all strains ε # εy
the stress is calculated as f = E ε. However, for strains greater than εy the stress is
equal to fy as shown in Figure 4. Thus, the resulting stress diagram is as shown in Figure
5c. Naturally, to evaluate the acting forces F1 and F2 and their location, the location x of
the yield strain εy must be known. From Figure 5c using similar triangles we have:
x c εy 0.00075
= . Thus x = c= 10 = 7.5in .
εy 0.001 0.001 0.001
Now the calculation of the magnitude and location of forces F1 and F2 becomes easy:
F1 = fy x 2.5 x 12 = 3 x 2.5 x 12 = 90 kips at a distance x1 = 7.5 + 2.5/2 = 8.75 in. from the
centroid.
F2 = ½ fy x 7.5 x 12 = ½ x 3 x 7.5 x 12 = 135 kips at a distance x2 = (2/3) 7.5 = 5 in. from
the centroid.
The moment on the cross-section is:
M = 2 A (F1 A x1 + F2 A x2) = 2 x (90 x 8.75 + 135 x 5) = 2925 in-k.
The corresponding curvature is κ = 0.001/10 = 0.0001 in-1.

3. Let M be even larger than in stage 2 above. The strains at the bottom and top fibers are
also larger (Figure 5d). For example, let ε = 0.002. At an inner location x the strain is
equal to εy. For all strains ε # εy the stress is calculated as f = E ε. Again, for strains
greater than εy the stress is equal to fy as shown in Figure 4. Thus, the resulting stress
diagram is as shown in Figure 5d. To evaluate the acting forces F1 and F2 and their
location, the location x of the yield strain εy must be known. From Figure 5d using similar
x c εy 0.00075
triangles we have: = . Thus x = c= 10 = 3.75 in .
ε y 0.002 0.002 0.002
Now the forces F1 and F2 can be calculated:
F1 = fy x 6.25 x 12 = 3 x 6.25 x 12 = 225 kips at a distance x1 =3.75 + 6.25/2 = 6.875 in.
from the centroid.

Page 4 January 14, 2010

 F2 = ½ fy x 3.75 x 12 = ½ x 3 x 3.75 x 12 = 67.5 kips at a distance x2 = (2/3) 3.75 = 2.5 in.
from the centroid.
The moment on the cross-section is:
M = 2 A (F1 A x1 + F2 A x2) = 2 x (225 x 6.875 + 67.5 x 2.5) = 3431.25 in-k.
The corresponding curvature is κ = 0.002/10 = 0.0002 in-1.

4. Finally consider the extreme case that the strains are so large that the stress
distribution is as shown in Figure 6. This state can only be achieved asymptotically. In
this case the forces F can be calculated as:
F = fy x 10 x 12 = 3 x 10 x 12 = 360 kips at a
distance x = 5 in. from the centroid.
The moment of the cross-section is:
Mult = 2 A (F A x) = 2 x (360 x 5) = 3600 in-k.
The corresponding curvature is that of infinite
strains. That is, κ = 4.

The Moment - Curvature relation can now be

plotted and is presented in Figure 7.
Figure 6

4000

3000
Moment (in-k)

2000

1000

0
0 0.0005 0.001 0.0015 0.002
Curvature (1/in)
Figure 7

Page 5 January 14, 2010

Inelastic Composite Example

Consider the composite cross-section shown in Figure 8. This belongs to a beam made out of a

Figure 8

material that is elastic in compression with modulus of elasticity E = 4000 ksi, and has no
strength in tension. To help the section carry bending, a blade of a metallic material is epoxied
at the bottom of the cross-section as shown. This material has a modulus of elasticity E =
20,000 ksi with a yield stress fy = 20 ksi. Thus the yield strain of the material is εy = 20/20,000
= 0.001.
Develop the M-κ relation of the cross-section.
It is common for such problems to replace the blade with only a line (i.e. no thickness) that is
located at the centroid of the cross-section (with the proper area of course). Thus, we can
substitute the actual cross section with the one shown in Figure 9. Note how the depth of the
new cross-section is 20.75 + 0.5/2 = 21 inches. To develop the moment - curvature (M-κ)
relation we shall try a number of strain values at the bottom fiber starting with the elastic limit
εb= 0.001.

Figure 9

1. εb= 0.001
This is the case of first yield. From similar triangles (Figure 9b) we find that
c
ε t = 0.001 . This results in the stress distribution shown in Figure 9c, and the couple of
21 − c

Page 6 January 14, 2010

 forces shown in Figure 9d. Since Fc is the resultant of the triangular distribution of
stresses we have: Fc = ½ 4000AεtA12Ac = ½A4000A0.001A12Ac2/(21-c) or Fc = 24Ac2/(21-c).
Equilibrium of forces requires that Fc = Ft = 120 kips. Thus we find: 24c2 + 120c - 2520 = 0.
The solution of this quadratic equation produces a negative and a positive root. Obviously,
we shall only accept the positive root: c=8.05 in. Since both Fc and Fc are equal to 120 kips,
we have a couple with a moment arm d=21-c/3 = 18.32 in. Thus the moment is
My = 120 x 18.32 = 2198 in-k and the corresponding curvature is κy = 0.001/(21-c)=7.7x10-5.

2. εb= 0.002
For any case of bottom fiber strain greater than 0.001 (Figure 9e) we have a stress diagram
as shown in Figure 9f. Note that since the strain at the bottom fiber (metallic material) is
greater than the yield strain, the corresponding stress is 20 ksi, and thus the corresponding
tensile force is 120 kips. Note that from similar triangles in the strain diagram (Fig. 9e) we
have that strain at the top fiber is εt = 0.002Ac/(21-c), and thus the stress at the top fiber
is fy = 4000Aεt = 8Ac/(21-c). Again, as in the case of εb= 0.001, the compressive force can be
calculated as Fc = ½ 4000AεtA12Ac = ½A4000A0.002A12Ac2/(21-c) or Fc = 48Ac2/(21-c). Equilibrium
of forces requires that Fc = Ft = 120 kips. Thus we find: 48c2 + 120c - 2520 = 0.
The solution of this quadratic equation produces a negative and a positive root. Obviously,
we shall only accept the positive root: c=6.1 in. Since both Fc and Fc are equal to 120 kips, we
have a couple with a moment arm d=21-c/3 = 18.97 in. Thus the moment is
M = 120 x 18.97 = 2276 in-k and the corresponding curvature is κ = 0.002/(21-c)=1.34x10-4.

Following a similar process we find that for

εb= 0.003 c = 5.175 in. M = 2313 in-k and κ = 0.000189
εb= 0.004 c = 4.575 in. M = 2337 in-k and κ = 0.000243
Note that as the strain at the bottom fiber increases, the location of the neutral axis moves
upwards. Asymptotically as εb tends to infinity c tends to 0 and the moment tends to 120 x 21 =
2520 in-k.
A plot of the moment vs curvature for this cross-section 2500
is presented in Figure 10.
2000
Moment (in-k)

1500

1000

500

0.0001 0.0002
Curvature (1/in.)

Figure 10

Page 7 January 14, 2010