Documenti di Didattica
Documenti di Professioni
Documenti di Cultura
Hca 1 LPP Sol
Caricato da
Manish SinghTitolo originale
Copyright
Formati disponibili
Condividi questo documento
Condividi o incorpora il documento
Hai trovato utile questo documento?
Questo contenuto è inappropriato?
Segnala questo documentoCopyright:
Formati disponibili
Hca 1 LPP Sol
Caricato da
Manish SinghCopyright:
Formati disponibili
Solution Sheet for Hard Copy Assignment-1(LPP)
BTech, 7th Sem, ME, 2019-20, Autumn Sem
1. Formulation of LPP Model :
Let x1 & x2 are kg of B1 & B2 to be produced per week and z= total profit per week, then the
given problem can be formulated as
Maximize z = 3x1+ 4x2
Subject to 3x1+ 2x2 ≤ 30
x1+ 2x2 ≤ 20
and x1, x2 ≥ 0
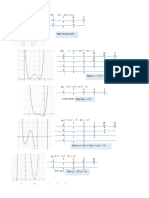
2. Solution of Q.1 by graphical method
3. Solution by graphical method:
Maximize z = 10x1+ 4x2
Subject to 3x1+ 2x2 ≤ 30
x1+ 2x2 ≤ 20
and x1, x2 ≥ 0
Ans:
As the Objective function line is shifted upwards & to right side starting from origin(0,
0) it will leave the feasible zone at last at point C. See the graph below. So, optimal point
is at C where x1=10 & x2 =0, so that z = 10x10+0 = 100
Dr. S.K. Patel, Mech Engg, NIT Rourkela 30-Aug-19 Page 1 of 15
4. Simplex
Maximize z = 2x1+ 3x2 + 4x3 z - 2x1 - 3x2 - 4x3 = 0 …..(0)
Subject to 2x1+ x2 + x3 ≤ 30 2x1+ x2 + x3 + s1 = 30 … (1)
x1+ 2x2 + x3 ≤ 20 x1+ 2x2 + x3 + s2 = 20…(2)
x1+ x2 + 2x3 ≤ 30 x1+ x2 + 2x3 + s3 = 30…(3)
and x1, x2, x3 ≥ 0 and x1, x2, x3, s1, s2, s3 ≥ 0
Eqn Basic z x1 x2 x3 s1 s2 s3 RHS Ratio Row Row operation
0 z 1 -2 -3 -4 0 0 0 0 10
1 s1 0 2 1 1 1 0 0 30 30 11
2 s2 0 1 2 1 0 1 0 20 20 12
3 s3 0 1 1 2 0 0 1 30 15 13
0 z 1 0 -1 0 0 0 2 60 20 row20=row10-(-4)xrow23
1 s1 0 1 1/2 1/2 0 1 0 - 1/2 15 30 21 row21=row11-1xrow23
2 s2 0 1/2 1 1/2 0 0 1 - 1/2 5 3 1/3 22 row22=row12-1xrow23
3 x3 0 1/2 1/2 1 0 0 1/2 15 30 23 row23=row13/2
0 z 1 1/3 0 0 0 2/3 1 2/3 63 1/3 30 row30=row20-(-1)xrow32
-
1 s1 0 1 1/3 0 0 1 1/3 - 1/3 13 1/3 31 row31=row21-(1/2)xrow32
2 x2 0 1/3 1 0 0 2/3 - 1/3 3 1/3 32 row32=row22/(3/2)
-
3 x3 0 1/3 0 1 0 1/3 2/3 13 1/3 33 row33=row23-(1/2)xrow32
Ans: z=63 1/3, x1=0, x2= 3 1/3, x3=13 1/3, s1=13 1/3, s2=s3=0
Dr. S.K. Patel, Mech Engg, NIT Rourkela 30-Aug-19 Page 2 of 15
Q.5 Solve Q.1 by Simplex
Maximize z = 3x1+ 4x2 z - 3x1 - 4x2 = 0 …..(0)
Subject to 3x1+ 2x2 ≤ 30 3x1+ 2x2 + s1 = 30 . (1)
x1+ 2x2 ≤ 20 x1+ 2x2 + s2 = 20…(2)
and x1, x2 ≥ 0 and x1, x2, s1, s2≥ 0
Eqn Basic z x1 x2 s1 s2 RHS Ratio Row Row operation
0 z 1 -3 -4 0 0 0 10
1 s1 0 3 2 1 0 30 15 11
2 s2 0 1 2 0 1 20 10 12
0 z 1 -1 0 0 2 40 20 row20=row10-(-4)xrow22
1 s1 0 2 0 1 -1 10 5 21 row21=row11-2xrow22
2 x2 0 1/2 1 0 1/2 10 20 22 row22=row12/2
0 z 1 0 0 1/2 1 1/2 45 30 row30=row20-(-1)xrow31
1 x1 0 1 0 1/2 - 1/2 5 31 row31=row21/2
2 x2 0 0 1 - 1/4 3/4 7 1/2 32 row32=row22/(3/2)
Ans: z= 45, x1= 5, x2= 7.5, s1= s2=0
Q.6 Degeneracy:
Maximize z = 3x1+ 5x2 => z-3x1-5x2 = 0 …...…..(0)
Subject to x1 + 3x2 ≤ 9 => x1 + 3x2+ s1 = 9 ……(1)
2x1 + x2 ≤ 3 => 2x1 + x2 + s2 = 3 ……(2)
and x1, x2 ≥ 0 => x1, x2, s1, s2 ≥ 0
Eqn Basic z x1 x2 s1 s2 RHS Ratio
0 z 1 -3 -5 0 0 0
1 s1 0 1 3 1 0 9 3
2 s2 0 2 1 0 1 3 3
Same ratio 3, Break the tie arbitrarily, select
0 z 1 -1 1/3 0 1 2/3 0 15
1 x2 0 1/3 1 1/3 0 3 9
2 s2 0 1 2/3 0 - 1/3 1 0 0
0 z 1 0 0 1 2/5 4/5 15
1 x2 0 0 1 2/5 - 1/5 3
2 x1 0 1 0 - 1/5 3/5 0
Ans: z=15, x2=3, x1=0, rest s1=s2=0; no improvement in z value in last two interations; its
degenerate solution as at least one of the basic variable i.e. x1 = 0
Dr. S.K. Patel, Mech Engg, NIT Rourkela 30-Aug-19 Page 3 of 15
Case-2: Break tie by selecting s2 in stead of s1 as both have same ratio 3
Eqn Basic z x1 x2 s1 s2 RHS Ratio
0 z 1 -3 -5 0 0 0
1 s1 0 1 3 1 0 9 3
2 s2 0 2 1 0 1 3 3
0 z 1 7 0 0 5 15
1 s1 0 -5 0 1 -3 0
2 x2 0 2 1 0 1 3
Ans: z1=15, s1=0, x2=3, x1=s2=0, i.e. same as earlier
Q.7 Alternate Optima:
Maximize z = 2x1+ 6x2 => z-2x1-6x2 = 0 ………(0)
Subject to x1 + 3x2 ≤ 6 => x1 + 3x2 +s1 = 6 ……(1) x1
+ x2 ≤ 5 => x1 + x2 +s2 = 5 …………………..(2)
and x1, x2 ≥ 0
Eqn Basic z x1 x2 s1 s2 RHS Ratio
0 z 1 -2 -6 0 0 0
1 s1 0 1 3 1 0 6 2
2 s2 0 1 1 0 1 5 5
0 z 1 0 0 2 0 12
1 x2 0 1/3 1 1/3 0 2 6
2 s2 0 2/3 0 - 1/3 1 3 4 1/2
Dr. S.K. Patel, Mech Engg, NIT Rourkela 30-Aug-19 Page 4 of 15
Optimal solution; z = 12,x2=2, s2=3 & x1=s1=0
Non-basic variable x1 has zero coefficient in z-row; Taking this as entering variable
Eqn Basic z x1 x2 s1 s2 RHS Ratio
0 z 1 0 0 2 0 12
1 x2 0 0 1 1/2 - 1/2 1/2
2 x1 0 1 0 - 1/2 1 1/2 4 1/2
Ans: This is also optimal sol with same z =12 but x1=9/2, x2=1/2, s1=s2=0
Q.8 Unbounded :
Maximize z = 3x1+2x2 => z-3x1-2x2=0 ………..(0)
Subject to 2x1 - x2 ≤ 10 => 2x1 - x2 +s1 = 10 ….(1)
x1 ≤ 10 => x1 +s2 = 10 ……….(2)
and x1, x2 ≥ 0
Eqn Basic z x1 x2 s1 s2 RHS Ratio
0 z 1 -3 -2 0 0 0
1 s1 0 2 -1 1 0 10 -10
2 s2 0 1 0 0 1 10 infinte
All constraint coefficients under non-basic variable x2 are 0 or –ve
=> Increasing x2 infinitely, no constraints are violated
=> Solution is unbounded in x2 direction
Dr. S.K. Patel, Mech Engg, NIT Rourkela 30-Aug-19 Page 5 of 15
Q.9 Infeasible Solution:
Maximize z = 3x1+4x2 x1+x2+s1 = 5 ………………………….(1)
Subject to x1 + x2 ≤ 5 2x1+3x2-s2+A=30 …………………….(2)
2x1 + 3x2 ≥ 30 (2)=> A = 30-2x1-3x2+s2
and x1, x2 ≥ 0 z = 3x1+4x2-MA
z = 3x1+4x2-M(30-2x1-3x2+s2)
= (2M+3)x1+(3M+4)x2-Ms2-30M
z – (2M+3)x1 – (3M+4)x2 +Ms2 = – 30M…..(0)
Eqn Basic z x1 x2 s1 s2 A Solution Ratio
0 z 1 -(2M+3) -(3M+4) 0 M 0 -30M
1 s1 0 1 1 1 0 0 5 5
2 A 0 2 3 0 -1 1 30 10
0 z 1 M+1 0 3M+4 M 0 20-15M
1 x2 0 1 1 1 0 0 5
2 A 0 -1 0 -3 -1 1 15
it's Psuedo-optimal solution as it falsely appears as an optimal solution; it's not feasible as there is at least
one artificial variable with value more than zero i.e. A = 15 here
Dr. S.K. Patel, Mech Engg, NIT Rourkela 30-Aug-19 Page 6 of 15
Q.10 Big M Method
Minimize z = 3x1+ x2
Subject to 2x1 + x2 = 2
3x1 + 2x2 ≥ 5
x1 + x2 ≤ 3
and x1, x2 ≥ 0
Solution 10: Maximize z1 = -z = -3x1-x2 …..(0)
2x1+x2+A1 = 2 .……(1)
3x1+2x2-s1 = 5 => s1= - 5, Infeasible, s1 can’t be basic variable
3x1+2x2-s1+A2 = 5 ……(2)
x1+x2+s2 = 3 …….(3)
and x1, x2, s1, s2, A1, A2 ≥ 0
Objective function must be modified as Maximize z1 = –3x1–x2–MA1–MA2, where M→ +∞
(1)=> 2x1+x2+A1 = 2 => A1= 2–2x1–x2
(2)=> 3x1+2x2–s1+A2 = 5 => A2 = 5–3x1–2x2+s1
Substituting values of A1 & A2 in objective equation (0) :
z1= –3x1–x2–M(2–2x1–x2) –M(5-3x1-2x2+s1)
z1=(–3+2M+3M)x1– (1+M+2M)x2– 2M– 5M– Ms1
z1– (5M–3)x1– (3M–1)x2+ Ms1= –7M …..(0)
z1-(5M-3)x1– (3M-1)x2 +Ms1 = –7M..(0)
2x1+ x2 +A1 = 2 …….(1)
3x1+ 2x2 – s1 +A2=5 …....(2)
x1+ x2 + s2 =3 …….(3)
Coefficients of IBFS
Eq Basic z1 x1 x2 s1 s2 A1 A2 RHS
0 z1 1 -(5M-3) -(3M-1) M 0 0 0 -7M
1 A1 0 2 1 0 0 1 0 2
2 A2 0 3 2 -1 0 0 1 5
3 s2 0 1 1 0 1 0 0 3
Dr. S.K. Patel, Mech Engg, NIT Rourkela 30-Aug-19 Page 7 of 15
Coefficients of
Eq Basic z1 x1 x2 s1 s2 A1 A2 RHS Ratio
0 z1 1 0 -(M+1)/2 M 0 (5M-3)/2 0 -2M-3
1 x1 0 1 1/2 0 0 1/2 0 1 2
2 A2 0 0 1/2 -1 0 -3/2 1 2 4
3 s2 0 0 1/2 0 1 -1/2 0 2 4
Coefficients of
Eq Basic z1 x1 x2 s1 s2 A1 A2 RHS
0 z1 1 (M+1) 0 M 0 (3M-1) 0 -(M+2)
1 x2 0 2 1 0 0 1 0 2
2 A2 0 -1 0 -1 0 -2 1 1
3 s2 0 -1 0 0 1 -1 0 1
No more –ve no. in z1-row, so stop.
Optimal solution is z1*=-(M+2);z = -z1* = M+2=2;x2*=2;A2*=1;s2*= 1 ;& the rest x1*=s1*=A1*=0
But, A2 = 1 ≠ 0; Appears to be optimal, But infeasible => Pseudo-optimal
Q.11 Big M Method
Maximize z = 3x1+ x2
Subject to 2x1 + x2 ≥ 2
3x1 + 2x2=6
x1 + x2 ≤ 3
and x1, x2 ≥ 0
Solution: Maximize z = 3x1+x2 …..(0)
2x1+x2-s1= 2 ⇒ s1= -2, Infeasible, s1 can’t be basic variable
So, 2x1+x2-s1+A1= 2 ……………..……………..(1)
3x1+2x2 = 6 ⇒ 3x1+2x2+A2 = 6 ………….…(2)
x1+x2+s2 = 3 ……………………….…………..….(3)
and x1, x2, s1, s2, A1, A2 ≥ 0
Objective function must be modified as
Maximize z = 3x1+x2–MA1–MA2, where M→ +∞
(1) ⇒ 2x1+x2-s1+A1 = 2 => A1= 2–2x1–x2+s1
(2) ⇒ 3x1+2x2+A2 = 6 => A2 = 6–3x1–2x2
Substituting values of A1 & A2 in objective equation (0) :
z= 3x1+x2–M(2–2x1–x2+s1) –M(6-3x1-2x2)
z=(3+2M+3M)x1 + (1+M+2M)x2– 2M– 6M– Ms1
z– (5M+3)x1– (3M+1)x2+ Ms1= –8M …..(0)
Coefficients of IBFS
Eq Basic z x1 x2 s1 s2 A1 A2 RHS
0 z 1 -(5M+3) -(3M+1) M 0 0 0 -8M
1 A1 0 2 1 -1 0 1 0 2
2 A2 0 3 2 -0 0 0 1 6
3 s2 0 1 1 0 1 0 0 3
Dr. S.K. Patel, Mech Engg, NIT Rourkela 30-Aug-19 Page 8 of 15
Coefficients of IBFS
Eq Basic z x1 x2 s1 s2 A1 A2 RHS Ratio
0 z 1 0 -(M-1)/2 -(3M+3)/2 0 (5M+3)/2 0 3-3M
1 x1 0 1 1/2 -1/2 0 1/2 0 1 -2
2 A2 0 0 1/2 3/2 0 -3/2 1 3 2
3 s2 0 0 1/2 1/2 1 -1/2 0 2 4
Coefficients of IBFS
Eq Basic z x1 x2 s1 s2 A1 A2 RHS
0 z 1 0 1 0 0 M M+1 6
1 x1 0 1 2/3 0 0 0 1/3 2
2 s1 0 0 1/3 1 0 -1 2/3 2
3 s2 0 0 1/3 0 1 0 -1/3 1
No more –ve no. in z1-row, so stop;
Optimal solution is z*= 6, x1*=2, s1*= 2, s2*= 1 ,& the rest x2*=A1*=A2*=0
12. Dual of dual is primal
Given LPP is
Minimize z = 3x1+ 2x2 + x3
Subject to
-3x1+ 3x2 + x3 ≥ 6
x1+ x2 + x3 = 3
and x1 is unrestricted in sign, and x2, x3 ≥ 0
Converting this to standard LPP form i.e. maximize subject to all ≤ constraints
Maximize -z = -3x1- 2x2 - x3
Subject to
3x1- 3x2 - x3 ≤ -6
x1+ x2 + x3 = 3
and x1 is unrestricted in sign, x2, x3 ≥ 0
Now Dual LPP is written as
Minimize zd = -6a +3b
Subject to 3a + b = -3
-3a +b ≥ -2
-a + b ≥ -1
a ≥ 0, b is unrestricted in sign
next to find dual of this LPP, again write it down in standard LPP form i.e., Maximize subject to
≤ constraints,
Maximize z1 = -zd = 6a -3b
Subject to -3a - b = 3
3a- b ≤ 2
a-b≤1
a ≥ 0, b is unrestricted in sign
Assuming x1, x2 and x3 as dual variables associated with three constraints
its dual will be written as:
Dr. S.K. Patel, Mech Engg, NIT Rourkela 30-Aug-19 Page 9 of 15
Minimize z = 3x1+2x2+x3
Subject to -3x1+3x2 +x3 ≥ 6
-x1-x2-x3 = -3 or, x1+x2+x3 = 3
and x1 is unrestricted in sign, x2 & x3 ≥ 0
This is the primal LPP given at the beginning.
Q.13 Solving its Dual
Find the solution of the following LPP by solving its dual with simplex method: Minimize z =
3x1+ 2x2 + x3 subject to 3x1+ x2 + x3 ≥ 3, -3x1+ 3x2 + x3 ≥ 6, x1+ x2 + x3 ≤ 3, and x1, x2,
x3 ≥ 0
Solution: Here, with little change it can be made to dual LPP form
Minimize z = 3x1+ 2x2 + x3
Subject to 3x1+ x2 + x3 ≥ 3 ….. a
-3x1+ 3x2 + x3 ≥ 6 …… b
-x1- x2 - x3 ≥ -3 …… c
and x1, x2, x3 ≥ 0
Write the dual of above LPP:
Maximize zd = 3a + 6b – 3c
Subject to 3a - 3b - c ≤ 3
a +3b - c ≤ 2
a+ b-c≤1
and a, b, c ≥ 0
Use slack variable & write in equation form
zd- 3a- 6b+ 3c = 0 ………..(0)
3a- 3b- c + sd1 = 3 ………..(1)
a+ 3b- c + sd2 = 2 ………..(2)
a+ b- c + sd3 = 1 ………..(3)
and a,b,c,sd1,sd2,sd3 ≥ 0
Solving by simplex method
Eq Basic zd a b c sd1 sd2 sd3 RHS Ratio
0 zd 1 -3 -6 3 0 0 0 0
1 sd1 0 3 -3 -1 1 0 0 3 -1
2 sd2 0 1 3 -1 0 1 0 2 2/3
3 sd3 0 1 1 -1 0 0 1 1 1
Eq Basic zd a b c sd1 sd2 sd3 RHS Ratio
0 zd 1 -1 0 1 0 2 0 4
1 sd1 0 4 0 -2 1 1 0 5 5/4
2 b 0 1/3 1 - 1/3 0 1/3 0 2/3 2
3 sd3 0 2/3 0 - 2/3 0 - 1/3 1 1/3 1/2
Eq Basic zd a b c sd1 sd2 sd3 RHS Ratio
0 zd 1 0 0 0 0 3/2 3/2 9/2
Dr. S.K. Patel, Mech Engg, NIT Rourkela 30-Aug-19 Page 10 of 15
1 sd1 0 0 0 2 1 3 -6 3
2 b 0 0 1 0 0 1/2 - 1/2 1/2
3 a 0 1 0 -1 0 - 1/2 3/2 1/2
Dual Optimal Sol: zd= 9/2, a=1/2, b= 1/2, c=0, sd1=3, sd2=sd3=0
Solution of Primal LPP using the coefficients of 0th row:
s1 = coefficient of a = 0; s2 = coefficient of b = 0; s3 = coefficient of c = 0; x1 = coefficient of sd1 = 0
x2 = coefficient of sd2 = 3/2; x3 = coefficient of sd3 = 3/2; z = zd = 9/2
Q.14 Dual Simplex
Minimize z = 3x1+ 2x2 + x3 maximize z1 = -z = -3x1- 2x2 -x3
Subject to 3x1+ x2 + x3 ≥ 3 Subject to 3x1+ x2 + x3 ≥ 3
-3x1+ 3x2 + x3 ≥ 6 -3x1+ 3x2 + x3 ≥ 6
x1+ x2 + x3 ≤ 3 x1+ x2 + x3 ≤ 3
and x1, x2, x3 ≥ 0 and x1, x2, x3 ≥ 0
Eqn Basic z1 x1 x2 x3 s1 s2 s3 RHS
0 z1 1 3 2 1 0 0 0 0
1 s1 0 -3 -1 -1 1 0 0 -3
2 s2 0 3 -3 -1 0 1 0 -6
3 s3 0 1 1 1 0 0 1 3
Ratio 2/3 1
0 z1 1 5 0 1/3 0 2/3 0 -4
1 s1 0 -4 0 - 2/3 1 - 1/3 0 -1
2 x2 0 -1 1 1/3 0 - 1/3 0 2
3 s3 0 2 0 2/3 0 1/3 1 1
Ratio 1 1/4 1/2 2
0 z1 1 3 0 0 1/2 1/2 0 -4 1/2
1 x3 0 6 0 1 -1 1/2 1/2 0 1 1/2
2 x2 0 -3 1 0 1/2 - 1/2 0 1 1/2
3 s3 0 -2 0 0 1 0 1 0
Ans: z= -z1= -(-4 1/2) = 9/2, x1=0, x2= 3/2, x3 = 3/2, s1=s2=s3=0
Q.15 Sensitivity Analysis:
z - 2x1 - 3x2 - 4x3 = 0 …..(0)
2x1+ x2 + x3 + s1 = 30 … (1)
Q.14 Maximize z = 2x1+ 3x2 + 4x3 x1+ 2x2 + x3 + s2 = 20… (2)
Subject to 2x1+ x2 + x3 ≤ 30 x1+ x2 + 2x3 + s3 = 30…(3)
x1+ 2x2 + x3 ≤ 20 and x1, x2, x3, s1, s2, s3 ≥ 0
x1+ x2 + 2x3 ≤ 30
and x1, x2, x3 ≥ 0
The final table showing optimal solution to above LPP is shown below:
Eqn Basic z x1 x2 x3 s1 s2 s3 RHS Ratio
0 z 1 1/3 0 0 0 2/3 1 2/3 63 1/3
1 s1 0 1 1/3 0 0 1 - 1/3 - 1/3 13 1/3
2 x2 0 1/3 1 0 0 2/3 - 1/3 3 1/3
3 x3 0 1/3 0 1 0 - 1/3 2/3 13 1/3
Dr. S.K. Patel, Mech Engg, NIT Rourkela 30-Aug-19 Page 11 of 15
Change in c_j if x_j is nonbasic
Let 2x1 is changed to 3x1 in Objective Function : Minimize z = 2x1+ 3x2 + 4x3
c1 = 2, c1n = 3
In optimal solution (final table) z1-c1 = coefficient of x1 in z-row = 1/3; z1-2 = 1/3, z1 = 2+1/3
new coeff of x1 in z-row = z1-c1n = 2+1/3-3 = -2/3; All other values remain unchanged
Eqn Basic z x1 x2 x3 s1 s2 s3 RHS Ratio
0 z 1 - 2/3 0 0 0 2/3 1 2/3 63 1/3
1 s1 0 1 1/3 0 0 1 - 1/3 - 1/3 13 1/3 10
2 x2 0 1/3 1 0 0 2/3 - 1/3 3 1/3 10
3 x3 0 1/3 0 1 0 - 1/3 2/3 13 1/3 40
0 z 1 0 2 0 0 2 1 70
1 s1 0 0 -4 0 1 -3 1 0
2 x1 0 1 3 0 0 2 -1 10
3 x3 0 0 -1 1 0 -1 1 10
Ans: z=70, x1=10, x2=0, x3=10, s1=s2=s3=0
Q.16 Change in c_j if x_j is basic
x2 is a basic variable in final table; Let 3x2 in Objective Function : Minimize z = 2x1+ 3x2 + 4x3 is changed to 2x2
so, c2 = 3 and c2n = 2
In optimal solution (final table) z2-c2 = coefficient of x2 in z-row = 0; z2-3 = 0, z2 = 3
new coeff = z2-c2n = 3-2 = 1; All other values remain unchanged
Eqn Basic z x1 x2 x3 s1 s2 s3 RHS Ratio
0 z 1 1/3 1 0 0 2/3 1 2/3 63 1/3
1 s1 0 1 1/3 0 0 1 - 1/3 - 1/3 13 1/3
2 x2 0 1/3 1 0 0 2/3 - 1/3 3 1/3
3 x3 0 1/3 0 1 0 - 1/3 2/3 13 1/3
Since, x2 is basic variable, its cofficients should be 0 in all rows except x2-row. But in z-row it's 1, so this is not
basic solution. So, eliminate x2 from eq(0) by subtracting eq(2) from eq(0).
Eqn Basic z x1 x2 x3 s1 s2 s3 RHS Ratio
0 z 1 0 0 0 0 0 2 60
1 s1 0 1 1/3 0 0 1 - 1/3 - 1/3 13 1/3
2 x2 0 1/3 1 0 0 2/3 - 1/3 3 1/3
3 x3 0 1/3 0 1 0 - 1/3 2/3 13 1/3
Ans: z=60, x1=0, x2=3 1/3, x3=13 1/3, s1=13 1/3, s2=s3=0
Q.17 Change in b_i
Let constraint (2) is changed from x1+ 2x2 + x3 ≤ 20 to x1+ 2x2 + x3 ≤ 13, thus b2= 20 is changed to b2n=13
Only RHS values of all rows will be affected. Slack variable for Constraint (2) is s2. So, (b2n-b) is multiplied with
coefficient of s2 of corresponding row and added to RHS of that row. For example, in eq(0) new RHS = 63 1/3 +
(2/3) (13-20), and then proceed.
Eqn Basic z x1 x2 x3 s1 s2 s3 RHS Ratio
0 z 1 1/3 0 0 0 2/3 1 2/3 58 2/3
1 s1 0 1 1/3 0 0 1 - 1/3 - 1/3 15 2/3
2 x2 0 1/3 1 0 0 2/3 - 1/3 -1 1/3
3 x3 0 1/3 0 1 0 - 1/3 2/3 15 2/3
Infeasible solution, so solving it by dual simplex method
Ratio 5
Dr. S.K. Patel, Mech Engg, NIT Rourkela 30-Aug-19 Page 12 of 15
Eqn Basic z x1 x2 x3 s1 s2 s3 RHS Ratio
0 z 1 2 5 0 0 4 0 52
1 s1 0 1 -1 0 1 -1 0 17
2 s3 0 -1 -3 0 0 -2 1 4
3 x3 0 1 2 1 0 1 0 13
Ans: z=52, x1=0, x2=0, x3=13, s1=17,s2=0,s3=4
Q.18 Change in a_ij if x_j is nonbasic
Let a31=1 in constraint (3) is changed to a31n=-1; thus x1+ x2 + 2x3 ≤ 30 is changed to -x1+ x2 + 2x3 ≤ 30,
change = a31n-a31= (-1) -(1) = -2
Like Q.5.c, only the coefficients under x1 will be changed by adding a multiple of corresponding coefficients of s3
i.e. the slack variable of 3rd constraint in which change has taken place. For ex.: in eq(0), new coeff = 1/3 + (1
2/3)(-2 )
Eqn Basic z x1 x2 x3 s1 s2 s3 RHS Ratio
0 z 1 -3 0 0 0 2/3 1 2/3 63 1/3
1 s1 0 2 0 0 1 - 1/3 - 1/3 13 1/3 6 2/3
2 x2 0 1 1 0 0 2/3 - 1/3 3 1/3 3 1/3
-13
3 x3 0 -1 0 1 0 - 1/3 2/3 13 1/3 1/3
it's now feasible but sub-optimal solution, so improve by simplex method
Eqn Basic z x1 x2 x3 s1 s2 s3 RHS Ratio
0 z 1 0 3 0 0 2 2/3 2/3 73 1/3
1 s1 0 0 -2 0 1 -1 2/3 1/3 6 2/3
2 x1 0 1 1 0 0 2/3 - 1/3 3 1/3
3 x3 0 0 1 1 0 1/3 1/3 16 2/3
Ans: z=73 1/3, x1=3 1/3, x2=0, x3=16 2/3, s1=6 2/3,s2=0,s3=0
Q.19 Change in a_ij if x_j is basic
Let a32=1 in constraint (3) is changed to a32n=2; thus x1+ x2 + 2x3 ≤ 30 is changed to x1+ 2x2 + 2x3 ≤ 30,
change = a32n-a32= 2-1 = 1
Like Q.5.d, only the coefficients under x2 will be changed by adding a multiple of corresponding coefficients of s3
i.e. the slack variable of 3rd constraint in which change has taken place. For ex.: in eq(0), new coeff = 0 + (1
2/3)(1 )
Eqn Basic z x1 x2 x3 s1 s2 s3 RHS Ratio
0 z 1 1/3 1 2/3 0 0 2/3 1 2/3 63 1/3
1 s1 0 1 1/3 - 1/3 0 1 - 1/3 - 1/3 13 1/3
2 x2 0 1/3 2/3 0 0 2/3 - 1/3 3 1/3
3 x3 0 1/3 2/3 1 0 - 1/3 2/3 13 1/3
x2 is a basic variable, do necessary gauss jordan row operations so that cofficients in x2 column {1 2/3, -1/3,
2/3, 2/3} will change to {0,0,1,0}
Eqn Basic z x1 x2 x3 s1 s2 s3 RHS Ratio
0 z 1 - 1/2 0 0 0 -1 2 1/2 55
1 s1 0 1 1/2 0 0 1 0 - 1/2 15 infinity
2 x2 0 1/2 1 0 0 1 - 1/2 5 5
3 x3 0 0 0 1 0 -1 1 10 -10
Eqn Basic z x1 x2 x3 s1 s2 s3 RHS Ratio
0 z 1 0 1 0 0 0 2 60
1 s1 0 1 1/2 0 0 1 0 - 1/2 15
2 s2 0 1/2 1 0 0 1 - 1/2 5
3 x3 0 1/2 1 1 0 0 1/2 15
Dr. S.K. Patel, Mech Engg, NIT Rourkela 30-Aug-19 Page 13 of 15
Ans: z=60, x1=x2=0, x3=15, s1=15, s2=s3=0
Q.20 Adding a new constraint
A new constraint x2+x3 ≤ 15 is added as 4th one, so add a new slack variable s4 to get 4th eqn as x2+x3+s4=15;
so add a new row and a new column for this as shown below; it's feasible, optimal but not basic as although x2
and x3 are basic variables they are present in s4 row, so eliminate them by gauss-jordan elimination
Eqn Basic z x1 x2 x3 s1 s2 s3 s4 RHS
0 z 1 1/3 0 0 0 2/3 1 2/3 0 63 1/3
1 s1 0 1 1/3 0 0 1 - 1/3 - 1/3 0 13 1/3
2 x2 0 1/3 1 0 0 2/3 - 1/3 0 3 1/3
3 x3 0 1/3 0 1 0 - 1/3 2/3 0 13 1/3
4 s4 0 0 1 1 0 0 0 1 15
Eqn Basic z x1 x2 x3 s1 s2 s3 s4 RHS
0 z 1 1/3 0 0 0 2/3 1 2/3 0 63 1/3
1 s1 0 1 1/3 0 0 1 - 1/3 - 1/3 0 13 1/3
2 x2 0 1/3 1 0 0 2/3 - 1/3 0 3 1/3
3 x3 0 1/3 0 1 0 - 1/3 2/3 0 13 1/3
4 s4 0 - 1/3 0 1 0 - 2/3 1/3 1 11 2/3
Eqn Basic z x1 x2 x3 s1 s2 s3 s4 RHS
0 z 1 1/3 0 0 0 2/3 1 2/3 0 63 1/3
1 s1 0 1 1/3 0 0 1 - 1/3 - 1/3 0 13 1/3
2 x2 0 1/3 1 0 0 2/3 - 1/3 0 3 1/3
3 x3 0 1/3 0 1 0 - 1/3 2/3 0 13 1/3
4 s4 0 - 2/3 0 0 0 - 1/3 - 1/3 1 -1 2/3
it's not feasible, so solve by dual simplex
Ratio 1/2 2 5
Eqn Basic z x1 x2 x3 s1 s2 s3 s4 RHS
0 z 1 0 0 0 0 1/2 1 1/2 1/2 62 1/2
1 s1 0 0 0 0 1 -1 -1 2 10
2 x2 0 0 1 0 0 1/2 - 1/2 1/2 2 1/2
3 x3 0 0 0 1 0 - 1/2 1/2 1/2 12 1/2
4 x1 0 1 0 0 0 1/2 1/2 -1 1/2 2 1/2
Ans: z=62 1/2, x1= x2= 2 1/2, x3=12 1/2, s1=10, s2=s3=s4=0
Dr. S.K. Patel, Mech Engg, NIT Rourkela 30-Aug-19 Page 14 of 15
Q.21
So z= -f – 45
Q.22
>> [x,fval,exitflag]=linprog(f, A,b,Aeq,beq,lb)
Result: x =[2.000; 0000] , so x1 = 2, x2 = 0
f = fval = -6, so z = -f = 6.
Dr. S.K. Patel, Mech Engg, NIT Rourkela 30-Aug-19 Page 15 of 15
Potrebbero piacerti anche
- Instructor's Manual to Accompany CALCULUS WITH ANALYTIC GEOMETRYDa EverandInstructor's Manual to Accompany CALCULUS WITH ANALYTIC GEOMETRYNessuna valutazione finora
- Problem 1Documento17 pagineProblem 1Roqaia AlwanNessuna valutazione finora
- HW Assignment 2: Simplex Method For Solving LP and LINDO: TRAN-650 Urban Systems EngineeringDocumento3 pagineHW Assignment 2: Simplex Method For Solving LP and LINDO: TRAN-650 Urban Systems EngineeringvamshiNessuna valutazione finora
- Assignment - Nourhan KhaledDocumento5 pagineAssignment - Nourhan KhaledNourhan KhaledNessuna valutazione finora
- Minimizacion y MaximizacionDocumento10 pagineMinimizacion y MaximizacionLaura ObandoNessuna valutazione finora
- Minimizacion y MaximizacionDocumento10 pagineMinimizacion y MaximizacionLaura ObandoNessuna valutazione finora
- Exercise Simplex MethodDocumento4 pagineExercise Simplex MethodLola CarolinaNessuna valutazione finora
- The Simplex Method: MAXIMIZATION: Z 2 X X X 10 X X 20 X 5 X, X, X 0Documento5 pagineThe Simplex Method: MAXIMIZATION: Z 2 X X X 10 X X 20 X 5 X, X, X 0Princess AmberNessuna valutazione finora
- Quiz1 SolDocumento10 pagineQuiz1 SolOjo JeremiahNessuna valutazione finora
- American University of Ras Al Khaimah Operations Research (MEPM 531) Midterm Exam - Fall 2020Documento14 pagineAmerican University of Ras Al Khaimah Operations Research (MEPM 531) Midterm Exam - Fall 2020Roqaia AlwanNessuna valutazione finora
- MATH 110 - BBIT211 - LINEAR ALGEBRA - Make-Up Assignment (2-2021)Documento9 pagineMATH 110 - BBIT211 - LINEAR ALGEBRA - Make-Up Assignment (2-2021)Kiki KymsNessuna valutazione finora
- Problem 3.50 (A) (B) : For The Vector Field EDocumento2 pagineProblem 3.50 (A) (B) : For The Vector Field EEric KialNessuna valutazione finora
- MS La Mod5Documento28 pagineMS La Mod5Shyme FritsNessuna valutazione finora
- Simplex Method of Maximization Problems Containing The Greater Than SymbolDocumento10 pagineSimplex Method of Maximization Problems Containing The Greater Than SymbolJohn Delacruz100% (1)
- Math 115-250 Module 6Documento3 pagineMath 115-250 Module 6Kevin Mark ProvendidoNessuna valutazione finora
- Dual Simplex Method For Solving The PrimalDocumento49 pagineDual Simplex Method For Solving The PrimalPotnuru VinayNessuna valutazione finora
- CalculusDocumento2 pagineCalculusTausif KhattakNessuna valutazione finora
- Haramaya University: College of Business and EconomicsDocumento48 pagineHaramaya University: College of Business and EconomicsYG DENessuna valutazione finora
- Lab 3 OR Operations ResearchDocumento15 pagineLab 3 OR Operations Researchbnzayd2005Nessuna valutazione finora
- Electiva 2Documento12 pagineElectiva 2Duvan SabogalNessuna valutazione finora
- LU DecompositionDocumento3 pagineLU DecompositionJairus Rodan CarinoNessuna valutazione finora
- Exam2 SolDocumento3 pagineExam2 SolMuhammad Enam ul HaqNessuna valutazione finora
- X X X X X X X X X XXX: Simplex Method Let Us Consider Again The Example of The Optimal Production Mix ProblemDocumento31 pagineX X X X X X X X X XXX: Simplex Method Let Us Consider Again The Example of The Optimal Production Mix ProblemSolomon AlemuNessuna valutazione finora
- (Cos (X) 1+co T (X) ) Cos (X) 1+ 1Documento3 pagine(Cos (X) 1+co T (X) ) Cos (X) 1+ 1Manuela CASTRO DIAZNessuna valutazione finora
- Simplex MethodDocumento2 pagineSimplex Methodمنار علي محسن 72 صباحيNessuna valutazione finora
- Menggunakan Metode Gauss: PersamaanDocumento4 pagineMenggunakan Metode Gauss: PersamaanGarry RamadhanNessuna valutazione finora
- Trabajo - Matrices - Matemáticas 1Documento4 pagineTrabajo - Matrices - Matemáticas 1Héctor Carrillo NúñezNessuna valutazione finora
- Hallar Si Es Posible: A) A.B XDocumento4 pagineHallar Si Es Posible: A) A.B XHéctor Carrillo NúñezNessuna valutazione finora
- Max Z 30x1+ 100x2: Thus The Objective Function IsDocumento5 pagineMax Z 30x1+ 100x2: Thus The Objective Function IsShakeel BhellarNessuna valutazione finora
- TugasDocumento11 pagineTugasQUrnia Wulan CucurNessuna valutazione finora
- The Diophane Equation x3 + Y3 2z2Documento8 pagineThe Diophane Equation x3 + Y3 2z2Anónimo PorsiacasoNessuna valutazione finora
- Assignment 1Documento7 pagineAssignment 1Tanjim RijuNessuna valutazione finora
- RR7 AlgebraDocumento2 pagineRR7 AlgebraCristina CarrilloNessuna valutazione finora
- Louis Ansis PerbaikanDocumento7 pagineLouis Ansis PerbaikanlouisNessuna valutazione finora
- A) X +10x 2 3x + X 6Documento2 pagineA) X +10x 2 3x + X 6Anonymous DzJo0vzNessuna valutazione finora
- Simplex Method Problem-SolvedDocumento3 pagineSimplex Method Problem-SolvedChandra Hasan0% (1)
- Model Answer 4 - MPZ 4230 - 2009Documento8 pagineModel Answer 4 - MPZ 4230 - 2009gayanlakNessuna valutazione finora
- Chapter3 - LP Algebraic SolutionDocumento5 pagineChapter3 - LP Algebraic Solutionabesmit1Nessuna valutazione finora
- Bresenham's Line AlgorithmDocumento22 pagineBresenham's Line AlgorithmNaman PatidarNessuna valutazione finora
- Ejercicios - Valores y Vectores PropiosDocumento20 pagineEjercicios - Valores y Vectores PropiosYARI DANELY GUEVARA LOPEZNessuna valutazione finora
- Examen FinalDocumento4 pagineExamen Finaloliver lopezNessuna valutazione finora
- Victorio Fatima Claire T. EE 3.4 MTH145Documento8 pagineVictorio Fatima Claire T. EE 3.4 MTH145Rundhille AndalloNessuna valutazione finora
- Taller Calculo FinalDocumento13 pagineTaller Calculo FinalRicardo Mojica CorreaNessuna valutazione finora
- Ceniza, Zenddy Crystal R. Bsee-4Se 1 A. 3x-Y - 6 B. 2x-Y 4 2x+3y 7 X+y 5 (-1,3) (3,2)Documento10 pagineCeniza, Zenddy Crystal R. Bsee-4Se 1 A. 3x-Y - 6 B. 2x-Y 4 2x+3y 7 X+y 5 (-1,3) (3,2)Zenddy CenizaNessuna valutazione finora
- Quiz10 SolutionsDocumento1 paginaQuiz10 SolutionsjamarosNessuna valutazione finora
- E G (X, Y) G (X, Y) ×F (X, Y) : Bivariate ExpectationDocumento17 pagineE G (X, Y) G (X, Y) ×F (X, Y) : Bivariate ExpectationKimondo KingNessuna valutazione finora
- Source PresentasiDocumento4 pagineSource PresentasiNur sohitNessuna valutazione finora
- 6.2 LessonDocumento6 pagine6.2 Lesson1020907Nessuna valutazione finora
- SOLUTIONS 2 Quadratic EquationsDocumento25 pagineSOLUTIONS 2 Quadratic EquationsVANDA CONSULTANTSNessuna valutazione finora
- Operation Research - MTH601 Fall 2007 Assignment 04 SolutionDocumento6 pagineOperation Research - MTH601 Fall 2007 Assignment 04 SolutionMARIA NINUNessuna valutazione finora
- Problem 3.51Documento1 paginaProblem 3.51Eric KialNessuna valutazione finora
- Sol GraficaDocumento5 pagineSol GraficaOscarPerezNessuna valutazione finora
- Sol GraficaDocumento5 pagineSol GraficaPepe B. DíazNessuna valutazione finora
- Solución GraficaDocumento5 pagineSolución GraficaOscarPerezNessuna valutazione finora
- Simplex Method Additional ActivityDocumento3 pagineSimplex Method Additional ActivityIra Grace De CastroNessuna valutazione finora
- Deriving Simpsons Rule Using Newton InterpolationDocumento4 pagineDeriving Simpsons Rule Using Newton InterpolationVinjkNessuna valutazione finora
- L32 - Quadratic Programming - Modified Simplex AlgorithmDocumento38 pagineL32 - Quadratic Programming - Modified Simplex AlgorithmNirmitNessuna valutazione finora
- MEtodo Dos FasesDocumento7 pagineMEtodo Dos FasesSergio LuqueNessuna valutazione finora
- Big M MethodDocumento4 pagineBig M MethodTempapara AccountakaraNessuna valutazione finora
- Si PDFDocumento1 paginaSi PDFStevan RiañoNessuna valutazione finora
- Brochure Thermoformer Range enDocumento52 pagineBrochure Thermoformer Range enJawad LOUHADINessuna valutazione finora
- Memory ManagmentDocumento3 pagineMemory ManagmentAmiraNessuna valutazione finora
- MNDALA-2 3 0-Change LogDocumento2 pagineMNDALA-2 3 0-Change LogJuani AriasNessuna valutazione finora
- Java Mock3Documento19 pagineJava Mock3rishiimcaNessuna valutazione finora
- VerizonWireless AffDocumento2 pagineVerizonWireless Affjbjkhb hibNessuna valutazione finora
- Iot Based Waste Collection Management System For Smart Cities: An OverviewDocumento4 pagineIot Based Waste Collection Management System For Smart Cities: An OverviewApurv ChoubeyNessuna valutazione finora
- CXCI Cordex 2v0 Quick RefDocumento2 pagineCXCI Cordex 2v0 Quick RefGuillermo OvelarNessuna valutazione finora
- Presentation For UCLDocumento33 paginePresentation For UCLabrahamaudu100% (1)
- MR SandeepDocumento2 pagineMR SandeepSameer NSNessuna valutazione finora
- Minh Nguyen ResumeDocumento2 pagineMinh Nguyen Resumeapi-537841053Nessuna valutazione finora
- Order Form - Biznet Dedicated Internet Maret 2020Documento11 pagineOrder Form - Biznet Dedicated Internet Maret 2020Wendi SopianNessuna valutazione finora
- DBM CSC FormDocumento4 pagineDBM CSC FormJing Goal Merit0% (1)
- Modelo Ecm370Documento420 pagineModelo Ecm370RENO100% (2)
- Robert Salisbury Email: Office: (713) - 462-5232 Ext.102Documento24 pagineRobert Salisbury Email: Office: (713) - 462-5232 Ext.102KaushikNessuna valutazione finora
- CatalogDocumento66 pagineCataloggmconNessuna valutazione finora
- StdoutDocumento2 pagineStdoutManuel MontesinosNessuna valutazione finora
- Nera Telecommunications LTD Annual Report 2019 PDFDocumento160 pagineNera Telecommunications LTD Annual Report 2019 PDFNipun SahniNessuna valutazione finora
- Laptop Use Policy FormDocumento2 pagineLaptop Use Policy FormVigNeshNessuna valutazione finora
- The PIECES FrameworkDocumento2 pagineThe PIECES Frameworkdivyashree1988Nessuna valutazione finora
- Core - Media and Information Literacy CG - WordDocumento17 pagineCore - Media and Information Literacy CG - WordMs. Rizza MagnoNessuna valutazione finora
- DTK Det DepDocumento49 pagineDTK Det DepJames SmithNessuna valutazione finora
- LOGO! Analog Input PT100 ManualDocumento6 pagineLOGO! Analog Input PT100 ManualKhurram100% (3)
- Gorm Day2Documento45 pagineGorm Day2Ryan SmithNessuna valutazione finora
- Round Your Answer Off To 4 Decimal Places: 2 PointsDocumento4 pagineRound Your Answer Off To 4 Decimal Places: 2 PointsPam MshweshweNessuna valutazione finora
- Windows 10 Guide PDFDocumento10 pagineWindows 10 Guide PDFAbeyMulugetaNessuna valutazione finora
- 271 7Documento0 pagine271 7Usman Sabir100% (1)
- HP Maintenance and Service GuideDocumento197 pagineHP Maintenance and Service GuideJulio Rafael GamboaNessuna valutazione finora
- Plagiarism - ReportDocumento13 paginePlagiarism - ReportGuddi ShelarNessuna valutazione finora
- IntroductionDocumento100 pagineIntroductionmadeeeNessuna valutazione finora
- Blockbash 2023 DocumentDocumento14 pagineBlockbash 2023 DocumentNessuna valutazione finora