Documenti di Didattica
Documenti di Professioni
Documenti di Cultura
Finding max and min points of functions
Caricato da
iqbal kurokoDescrizione originale:
Titolo originale
Copyright
Formati disponibili
Condividi questo documento
Condividi o incorpora il documento
Hai trovato utile questo documento?
Questo contenuto è inappropriato?
Segnala questo documentoCopyright:
Formati disponibili
Finding max and min points of functions
Caricato da
iqbal kurokoCopyright:
Formati disponibili
6.
3 Optimisation for Functions of One Variable
6.3.1 Slope of a curve and turning points
Optimisation is mainly concerned with finding maximum and minimum points, also known
as stationary points, on a curve. Applications include finding maximum and minimum values for
functions such as profit, cost, utility and production.
Remember, the slope of the curve at a point is the same as the slope of the tangent at that
point. Figure 6.12 shows four turning points, two minima and two maxima, with the tangents
drawn at these points. Note these are called 'local' minimum and maximum points as opposed to
'global' or absolute minimum and maximum points.
In Figure 6.12 the tangents drawn at the turning points are horizontal, so they have no
slope; that is, slope = 0. One can prove, with calculus that at turningpoints theslope of a curve is
alwayszero. This fact provides the key to finding the exact coordinates of turning points.
The argument is as follows:
• We know that dy/dx gives the equation for slope at any point (x,y).
• We know slope = 0 at turningpoints.
• So,dy/dx= 0 at turning points
Therefore, to find the x-coordinates of the turning
points for a curve y = f(x), the following method
is used:
Step 1: Find dy/dx for the given curve y = f(x).
Step 2: Solve the equation dy/dx = 0.
The solution of this equation gives the x-
coordinates of the turning points. Notes
(i) If the equation dy/dx = 0 has no solution, then
there is no turning point,
(ii) While it is true that at turning points we can
say dy/dx = 0, the converse is not always true. If
dy/dx0 at a point, it may indeed be a turning point
but it could be a point of inflection.
Table 6.7 briefly outlines some other terminology that is commonly used in optimisation.
Example 6.16
6.3.2 Determining maximum and minimum turning points
The next step is to determine whether each turning point is a maximum or a minimum. We
could of course plot the graphs, since we know the precise turning points as in Figure 6.13, but
this is time-consuming and not practical in the long term. Before proceeding to a method that will
enable us to determine whether a point is a maximum or a minimum, here are some points to note.
Testing for minimum and maximum points
Figure 6.15 illustrates how slope changes as we move through maximum and minimum points.
As we move through a maximum point, illustrated in Figure 6.15(a), the slope v' changes
from being positive before the maximum (as y increases towards the maximum), zero at
the maximum and negative after the maximum (as y decreases down from the maximum).
As we move through a minimum point, illustrated in Figure 6.15(b) the slope v' changes
from being negative before the minimum (as v decreases down to the minimum),zero at
the minimum and positive after (as y increases away from the minimum).
This behaviour provides two methods of determining whether a turning point is a maximum
or a minimum. Start by calculating the value of x at which dy/dx = 0. Call this value x = 0. Also
determine d2x/dy2 and evaluate it at X0. This is written symbolically as
Potrebbero piacerti anche
- MC Ty Maxmin 2009 1 PDFDocumento10 pagineMC Ty Maxmin 2009 1 PDFRahul SinghNessuna valutazione finora
- Finding Stationary Points Using DifferentiationDocumento9 pagineFinding Stationary Points Using DifferentiationKeri-ann MillarNessuna valutazione finora
- AMSG.15.Applications of DifferentiationDocumento9 pagineAMSG.15.Applications of DifferentiationSalman 1stINANessuna valutazione finora
- MC TY Maxmin 2009 1Documento10 pagineMC TY Maxmin 2009 1Sajida CheemaNessuna valutazione finora
- Module 8 Applications (Handout)Documento14 pagineModule 8 Applications (Handout)Lyka Soriano MopasNessuna valutazione finora
- Presentation 1Documento10 paginePresentation 1Harraz AdliNessuna valutazione finora
- Applications of Differentiation 1. Tangents and NormalsDocumento13 pagineApplications of Differentiation 1. Tangents and NormalsronnieNessuna valutazione finora
- Non Linear Dynamics PDFDocumento8 pagineNon Linear Dynamics PDFMukesh KarunanethyNessuna valutazione finora
- STEP Support Programme STEP 2 Curve Sketching Topic NotesDocumento3 pagineSTEP Support Programme STEP 2 Curve Sketching Topic NotesHaoyu WangNessuna valutazione finora
- Chapter 2 Geometrical Applications of CalculusDocumento54 pagineChapter 2 Geometrical Applications of CalculusRhea0% (1)
- Diverg and Maxwell's First EqDocumento16 pagineDiverg and Maxwell's First EqBilal AhmedNessuna valutazione finora
- Derivative Definition ExplainedDocumento14 pagineDerivative Definition ExplainedGhoor DhdhfNessuna valutazione finora
- c1 7 DifferentiationDocumento45 paginec1 7 DifferentiationCallista Low100% (1)
- Full Hand OutDocumento35 pagineFull Hand OutOlusoji OriowoNessuna valutazione finora
- Curves, Lengths, Surfaces and AreasDocumento11 pagineCurves, Lengths, Surfaces and AreasRoy VeseyNessuna valutazione finora
- AddMathLesson (5th Form Term 1, Lesson 26 - Theoretical Applications of The Derivative)Documento6 pagineAddMathLesson (5th Form Term 1, Lesson 26 - Theoretical Applications of The Derivative)The MathematicianNessuna valutazione finora
- Appendix A 2Documento6 pagineAppendix A 2ErRajivAmieNessuna valutazione finora
- Lecture 11: Application of Derivative: DT DVDocumento12 pagineLecture 11: Application of Derivative: DT DVCapt John Daniel KamuliNessuna valutazione finora
- Presentation 2Documento15 paginePresentation 2Kushal BhattaraiNessuna valutazione finora
- Finding Maximum and Minimum of A FunctionDocumento17 pagineFinding Maximum and Minimum of A FunctionSultan MorseanNessuna valutazione finora
- C1.7 DifferentiationDocumento45 pagineC1.7 DifferentiationThomas GuoNessuna valutazione finora
- Chapter 2 Geometrical Applications of CalculusDocumento54 pagineChapter 2 Geometrical Applications of Calculusapi-236842331Nessuna valutazione finora
- CH 2Documento52 pagineCH 2SarahChahineNessuna valutazione finora
- CALCULATING RATES OF CHANGEDocumento14 pagineCALCULATING RATES OF CHANGEWuey MeiiNessuna valutazione finora
- Linearization of Differential Equation Models: 1 MotivationDocumento13 pagineLinearization of Differential Equation Models: 1 MotivationArindam PaulNessuna valutazione finora
- Increasing and Decreasing Functions (Lec 13)Documento35 pagineIncreasing and Decreasing Functions (Lec 13)Islamic Center worldNessuna valutazione finora
- Calculus I Chapter 4 IntegralsDocumento114 pagineCalculus I Chapter 4 IntegralsLong Phan DuyNessuna valutazione finora
- Introducing Differentiation: PrerequisitesDocumento14 pagineIntroducing Differentiation: PrerequisitesShrishail SambanniNessuna valutazione finora
- Derivative As Rates of Change - Population Change: Word ProblemDocumento6 pagineDerivative As Rates of Change - Population Change: Word ProblemAaron Paul CasabarNessuna valutazione finora
- Differential Equations 2011-06-24 1 Slide Per PageDocumento90 pagineDifferential Equations 2011-06-24 1 Slide Per PageBoldie LutwigNessuna valutazione finora
- DiffformsDocumento34 pagineDiffformsjuans_osNessuna valutazione finora
- Curving Sketching Using Calculus: Jackie NicholasDocumento11 pagineCurving Sketching Using Calculus: Jackie NicholasalyssaNessuna valutazione finora
- Basics of Hyperbolic GeometryDocumento4 pagineBasics of Hyperbolic Geometry21260paco61Nessuna valutazione finora
- Project 4 - Implicit Differentiation/Linear Approximations/LimitsDocumento2 pagineProject 4 - Implicit Differentiation/Linear Approximations/Limitsmasyuki1979Nessuna valutazione finora
- L'Hospital's rule for multivariable limitsDocumento13 pagineL'Hospital's rule for multivariable limitsAlonso Pablo Olivares LagosNessuna valutazione finora
- Numerical Methods - Fixed Point IterationDocumento4 pagineNumerical Methods - Fixed Point IterationMizanur RahmanNessuna valutazione finora
- Curves, Lengths, Surfaces and AreasDocumento11 pagineCurves, Lengths, Surfaces and AreasstriaukasNessuna valutazione finora
- Curvature: PrerequisitesDocumento14 pagineCurvature: PrerequisitesmathplazaNessuna valutazione finora
- Documents - MX Assignment-AdvanceDocumento30 pagineDocuments - MX Assignment-AdvanceMiu MakriNessuna valutazione finora
- HSC Maths Ext1 CH2Documento54 pagineHSC Maths Ext1 CH2moustafasadek11Nessuna valutazione finora
- Wang 1969Documento7 pagineWang 1969Haytham BouzidNessuna valutazione finora
- 7 CurvesDocumento42 pagine7 Curvesshealtielchigariso06Nessuna valutazione finora
- CG Chapter 5Documento61 pagineCG Chapter 5kiramelaku1Nessuna valutazione finora
- E0005E - Industrial Image Analysis: The Hough Transform Matthew ThurleyDocumento26 pagineE0005E - Industrial Image Analysis: The Hough Transform Matthew ThurleyNorbey Marin MorenoNessuna valutazione finora
- PG 2Documento1 paginaPG 2atharvnetke9Nessuna valutazione finora
- Maxima and Minima 2024Documento8 pagineMaxima and Minima 2024Vince Leo Panoncillon GonzalesNessuna valutazione finora
- Mathematics - Area Under The CurveDocumento43 pagineMathematics - Area Under The Curvedeepak876100% (1)
- Applications of Derivaties (Lec # 13)Documento36 pagineApplications of Derivaties (Lec # 13)Wajahat KhanNessuna valutazione finora
- U1_GradientsDocumento2 pagineU1_GradientsRanaNessuna valutazione finora
- 11 1 Intro DiffrntiatnDocumento10 pagine11 1 Intro DiffrntiatnEricGoballaNessuna valutazione finora
- Slides ChIV Bài 5. Vẽ Đồ Thị Hàm SốDocumento28 pagineSlides ChIV Bài 5. Vẽ Đồ Thị Hàm Sốlehoangsand55Nessuna valutazione finora
- Conic Sections The ParabolaDocumento16 pagineConic Sections The ParabolaAvinash kumar SinghNessuna valutazione finora
- Changing Coordinates: HELM (2005) : Workbook 27: Multiple IntegrationDocumento18 pagineChanging Coordinates: HELM (2005) : Workbook 27: Multiple IntegrationEbookcrazeNessuna valutazione finora
- AP Calc AB Limits DefsDocumento4 pagineAP Calc AB Limits DefsKohji Ashitaka SugiokaNessuna valutazione finora
- AP Calculus AB - Ultimate Guide Notes - KnowtDocumento29 pagineAP Calculus AB - Ultimate Guide Notes - Knowtcondyerhaze1Nessuna valutazione finora
- notesForCalc2 Curves 20221202Documento36 paginenotesForCalc2 Curves 20221202Vinicius BrunoNessuna valutazione finora
- Cambridge Mathematics AS Level Course: Second EditionDa EverandCambridge Mathematics AS Level Course: Second EditionNessuna valutazione finora
- A-level Maths Revision: Cheeky Revision ShortcutsDa EverandA-level Maths Revision: Cheeky Revision ShortcutsValutazione: 3.5 su 5 stelle3.5/5 (8)
- The Relationship Between Dissociation and Voices: A Systematic Literature Review and Meta-AnalysisDocumento52 pagineThe Relationship Between Dissociation and Voices: A Systematic Literature Review and Meta-Analysiseduardobar2000100% (1)
- List of TNA MaterialsDocumento166 pagineList of TNA MaterialsRamesh NayakNessuna valutazione finora
- Preparation Total Consecration PDFDocumento872 paginePreparation Total Consecration PDFgbarcelonNessuna valutazione finora
- WFISD Agenda Special SessionDocumento1 paginaWFISD Agenda Special SessionDenise NelsonNessuna valutazione finora
- ALL INDIA NURSING TEST REVIEWDocumento102 pagineALL INDIA NURSING TEST REVIEWDr-Sanjay SinghaniaNessuna valutazione finora
- Hamlet Act 3 Scene 1Documento4 pagineHamlet Act 3 Scene 1Αθηνουλα ΑθηναNessuna valutazione finora
- Department of Information TechnologyDocumento1 paginaDepartment of Information TechnologyMuhammad ZeerakNessuna valutazione finora
- Mini Test 1 AnswersDocumento4 pagineMini Test 1 AnswersMai Linh ThânNessuna valutazione finora
- Montes Del Plata Supervisory Training: PTS2Documento16 pagineMontes Del Plata Supervisory Training: PTS2sersehNessuna valutazione finora
- Dentsply Sirona Q2 Earnings Presentation - FINALDocumento18 pagineDentsply Sirona Q2 Earnings Presentation - FINALmedtechyNessuna valutazione finora
- Sid The Science Kid - The Ruler of Thumb Cd1.avi Sid The Science Kid - The Ruler of Thumb Cd2.aviDocumento27 pagineSid The Science Kid - The Ruler of Thumb Cd1.avi Sid The Science Kid - The Ruler of Thumb Cd2.avisheena2saNessuna valutazione finora
- Quieting of TitleDocumento11 pagineQuieting of TitleJONA PHOEBE MANGALINDANNessuna valutazione finora
- CRCT Probe 2011Documento300 pagineCRCT Probe 2011huffpostNessuna valutazione finora
- LAB REPORT-Osbourne Reynolds ApparatusDocumento20 pagineLAB REPORT-Osbourne Reynolds Apparatusmizizasbonkure9055% (11)
- I FlyDocumento2 pagineI Flyd_lee1883725Nessuna valutazione finora
- Quantum Mechanics and PeriodicityDocumento51 pagineQuantum Mechanics and Periodicitynxumalopat2Nessuna valutazione finora
- Chain of Custody Requirement in Drug CasesDocumento23 pagineChain of Custody Requirement in Drug CasesMiw CortesNessuna valutazione finora
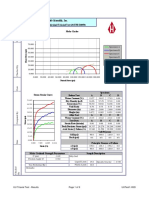
- Humboldt Scientific, Inc.: Normal Stress (Psi)Documento9 pagineHumboldt Scientific, Inc.: Normal Stress (Psi)Dilson Loaiza CruzNessuna valutazione finora
- Wonderland Staking and Minting Calculator (4,4)Documento8 pagineWonderland Staking and Minting Calculator (4,4)Dina Maya0% (4)
- World War 2 Facts Tell Us About A Bloody Conflict That Involved All The Nations of The WorldDocumento2 pagineWorld War 2 Facts Tell Us About A Bloody Conflict That Involved All The Nations of The WorldSaikumarVavilaNessuna valutazione finora
- Informative Speech 2010 (Speaking Outline) 2Documento5 pagineInformative Speech 2010 (Speaking Outline) 2FaranzaSynsNessuna valutazione finora
- Magic Writ: Textual Amulets Worn On The Body For Protection: Don C. SkemerDocumento24 pagineMagic Writ: Textual Amulets Worn On The Body For Protection: Don C. SkemerAsim HaseljicNessuna valutazione finora
- SkipTheFlip Physical PDFDocumento230 pagineSkipTheFlip Physical PDFSebi100% (4)
- SM pc300350 lc6 PDFDocumento788 pagineSM pc300350 lc6 PDFGanda Praja100% (2)
- Page - 1Documento18 paginePage - 1Julian Adam Pagal75% (4)
- English Language (1122)Documento26 pagineEnglish Language (1122)TD X Mzinda100% (1)
- 2004 Swamee, Prabhata K. Rathie, Pushpa N. - Exact Solutions For Normal Depth ProblemDocumento9 pagine2004 Swamee, Prabhata K. Rathie, Pushpa N. - Exact Solutions For Normal Depth Problemjosue.angelo9459Nessuna valutazione finora
- This Judgemen T Ranked 1 in The Hitlist.: Doc Id # 66804Documento19 pagineThis Judgemen T Ranked 1 in The Hitlist.: Doc Id # 66804Kapil DemlaNessuna valutazione finora
- ABC Pre School: (Please Refer Advertisement in This Section)Documento5 pagineABC Pre School: (Please Refer Advertisement in This Section)hemacrcNessuna valutazione finora
- Person On The StreetDocumento12 paginePerson On The StreetalyssajdorazioNessuna valutazione finora