NAME:_______________________________________________SCORE:__________

YEAR & SECTION:__________________________DATE CHECKED:_____________

CHAPTER 2: RATIONAL FUNCTIONS

2.1 RECALL
Definition:
A polynomial function p of degree n is a function that can be written in the form 𝑝(𝑥) =
𝑎𝑛 𝑥 𝑛 + 𝑎𝑛−1 𝑥 𝑛−1 + 𝑎𝑛−2 𝑥 𝑛−2 + ⋯ + 𝑎1 𝑥 + 𝑎0 where 𝑎0 , 𝑎1 , … , 𝑎𝑛 ∈ ℝ, 𝑎𝑛 ≠ 0, and 𝑛 ∈ ℤ+ .
Each summand is a term of the polynomial function. The constants 𝑎0 , 𝑎1 , … , 𝑎𝑛 are what
we called coefficients. The leading term is the term with the highest degree of exponent,
the leading coefficient is the coefficient of the leading term, and the constant term is
the term without a variable.

2.2 RATIONAL EQUATION, RATIONAL INEQUALITY, & RATIONAL FUNCTION

Definition:
A rational expression is an expression that can be written as a ratio of two polynomials.
Keep in mind that a rational expression can be described as a function where either the
numerator, denominators, or both have a variable on it.
Examples:

RATIONAL RATIONAL RATIONAL

EQUATION INEQUALITY FUNCTION
An equation An inequality a function of the
involving rational involving rational form 𝑝(𝑥)
Definition 𝑓(𝑥) = 𝑞(𝑥)
expressions expressions
where 𝑝(𝑥) and
𝑞(𝑥) are polynomial
DBAG: GENERAL MATHEMATICS 1
 functions, and
𝑞(𝑥) ≢ 0. The
domain of 𝑓(𝑥) is all
values of x where
𝑞(𝑥) ≠ 0.
8 𝑥 5 𝑓(𝑥) = 5𝑥 − 2 or
Example −8= ≥0
𝑥 2𝑥 − 1 𝑥+3 𝑦 = 5𝑥 − 2

Remember:
 A rational equation or inequality can be solved for all x values that satisfy the
equations or inequality.
 We do not solve rational functions. Instead, a rational function expresses a
relationship between two variables (such as x and y), and can be represented by
a table of values or a graph.

2.3 SOLVING RATIONAL EQUATIONS AND INEQUALITIES

A. Procedure for Solving Rational Equations
(a) Eliminate denominators by multiplying each term of the equation by at least common
denominator.
(b) Note that eliminating denominators may introduce “extraneous” solutions. Check the
solutions of the transformed equations with the original equation.

B. Procedure for Solving Rational Inequalities

(a) Rewrite the inequality as a single fraction on one side of the inequality symbol and 0
on the other side.
(b) Determine over what intervals the fraction takes on positive and negative values.
i. Locate the x-values for which the rational expression is zero or undefined.
ii. Mark the numbers found in (i) on a number line. Use a shaded circle or
parentheses, “( or )”, to indicate that the value is excluded. Theses numbers partition the
numerator line into intervals.
iii. Select a test point within the interior of each intervals in (ii). The sign of the
rational expression at this point is also the sign of the rational expression at each interior
point in the aforementioned interval.
iv. Summarize the intervals containing the solutions.
Remember:
 It is not valid to multiply both sides of an inequality by a variable since the sign of
the variable is unknown.
 Multiplying both sides of an inequality by a positive number retains the direction of
the inequality.

DBAG: GENERAL MATHEMATICS 2

 Multiplying both sides of an inequality by a negative number reverses the direction
of the inequality.

ACTIVITY 2.1
Direction: Solve the following rational equations. Write your solution inside the box.
𝑥 1 5 25 25 2
1. + 5 = 𝑥−5 2. − 𝑎−2 = 𝑎
𝑥−5 𝑎

𝑡 𝑥 72
3. − 12𝑡 −1 = 0 4. = 𝑥 2 −36 + 4
3 𝑥+6

DBAG: GENERAL MATHEMATICS 3

5. The shadow cast by a 3-meter stick is 4
meters long. The shadow cast by a
sycamore tree is 9 meters long. Find the
height of the sycamore tree. Assume that
the measurements were taken at the
same time of day.
7. Marceline drives 50 mi to a train station
and then continues her trip with 210-mi
train ride. The car travels 20 mph slower
than the train. If the total travel time is 4
hr, find the average speed of the car and
the average speed of the train.
6. Finn can wallpaper a bathroom in 3
hours. Jake can wallpaper the same
bathroom in 5 hours. How long would it
take them if they worked together?
8. The ratio of mages and knights in the
Kingdom of Lioness is 3:11. If the total
number of mages and knights is 112,
how many are mages and how many are
knights?
DBAG: GENERAL MATHEMATICS 4
ACTIVITY 2.2
Direction: Solve each of the following inequalities. Write your solution inside the box.
𝑥−1 −𝑥−8
1. >0 2. ≥5
𝑥 𝑥−2

3𝑥−1 2 3
3. ≤ −1 4. ≥4
𝑥 𝑥−1

DBAG: GENERAL MATHEMATICS 5

 3𝑥+6 𝑥+3
5. ≤0 6. ≤4
2𝑥−12 5−2𝑥

−2𝑥+5 2
7. > −2 8. ≤1
𝑥+6 𝑥+3

DBAG: GENERAL MATHEMATICS 6

2.4 GRAPHING RATIONAL FUNCTIONS
Definition: The vertical line x=a is a vertical asymptote of a function f if the graph of f
either increases or decreases without a bound as the x-value approach a from the right
or left.
How to find vertical asymptotes of a rational function?
 Reduce the rational function to lowest terms by cancelling out the common
factor/s in the numerator and denominator.
 Find the value a that will make the denominators of the reduced rational
function equal to zero.
 The line x=a is a vertical asymptote.

Definition: The horizontal line y=b is a horizontal asymptote of the function f if f(x) gets
closer to b as x increases or decreases without bound (𝑥 → +∞ 𝑜𝑟 𝑥 → −∞).
How to find horizontal asymptotes of a rational function?
Let n be the degree of the numerator and m be the degree of the denominator:
 If 𝑛 < 𝑚, the horizontal asymptote is 𝑦 = 0.
𝐴
 If 𝑛 = 𝑚, the horizontal asymptote is 𝑦 = 𝐵, where 𝐴 is the leading coefficient
of the numerator and 𝐵 is the leading coefficient of the denominator.
 If 𝑛 > 𝑚, there is no horizontal asymptote.

Steps in graphing rational functions

 Find the intercepts, if there are any.
 Find the vertical asymptote by setting the denominator to zero and solving.
 Find the horizontal asymptote using the degree of the polynomial in the numerator
and denominator, as indicated above.
 The vertical asymptotes will divide the number line into regions. In each region,
graph at least one point. This point will tell us whether the graph will be above or
below the x-axis and if we need to, we should get several points to determine the
general shape of the graph.
 Sketch the graph.
 Determine the domain by finding all x values which do not make the denominator
0 and the range by looking at the graph of the function.

ACTIVITY 2.3
Direction: Sketch the graph of the following rational functions and find its domain and
range.
8 𝑥 2 −3𝑥
1. 𝑓(𝑥) = 𝑥 2 −𝑥−6 3. 𝑓(𝑥) = 2𝑥 2 +2𝑥−12
1 4
2. 𝑓(𝑥) = −𝑥+4 4. 𝑓(𝑥) = 𝑥−3

DBAG: GENERAL MATHEMATICS 7

DBAG: GENERAL MATHEMATICS 8
NAME:_______________________________________________SCORE:__________
YEAR & SECTION:__________________________DATE CHECKED:_____________

CHAPTER 3: ONE-TO-ONE AND INVERSE FUNCTIONS

3.1 DEFINITION OF ONE-TO-ONE FUNCTION
Definition:
A function f is said to be one-to-one if for any 𝑥1 , 𝑥2 in the domain of f, then 𝑓(𝑥1 ) ≠ 𝑓(𝑥2 ).
That is, the same y-value is NEVER paired with two different x-values.

3.2 GRAPHS OF A ONE-TO-ONE FUNCTIONS

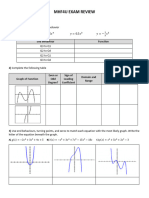
Look at the graphs below. Determine each graph if it is one-to-one or not.

𝑦 = 𝑥2 − 4 𝑦 = 𝑥3

2𝑥 + 3
𝑦=
𝑦 = 2𝑥 − 1 𝑥

DBAG: GENERAL MATHEMATICS 9

A simple way to determine if a given graph is a one-to-one function is through the use of
Horizontal Line Test.

Horizontal Line Test

A function is one-to-one if each horizontal line does not intersect the graph at more
than one point.

Remember: All functions satisfy the vertical line test. All one-to-one function satisfy
BOTH the vertical and horizontal line tests.

3.3. INVERSE OF ONE-TO-ONE FUNCTIONS

Inverting Functions
 If x- and y- values of a one-to-one function are interchanged, the result is a function
but,
 If x- and y- values of a function that is not one-to-one are inverted, the result is no
longer a function.
Definition:
Let 𝑓 be a one-to-one function with a domain A and range B. Then the inverse of 𝑓,
denoted by 𝑓 −1 , is a function with a domain B and range A defined by 𝑓 −1 (𝑦) = 𝑥 if and
only if 𝑓(𝑥) = 𝑦 for any 𝑦 in B.
Remember: A function has an inverse if and only if it is one-to-one.

Steps in determining the inverse of a function from its equation

 Write the function in the form of 𝑦 = 𝑓(𝑥);
 Interchanged the x and y variables;
 Solve for y in terms of x.

Question:
What is the inverse of the inverse? What is the composite function of a given one-
to-one function and its inverse?

DBAG: GENERAL MATHEMATICS 10

ACTIVITY 3.1
Direction: Find the inverse of the following one-to-one function.
3
1. 𝑓 (𝑥) = (𝑥 + 3)3 2. 𝑓 (𝑥) =
𝑥−4

𝑥+3 2𝑥+1
3. 𝑓 (𝑥) = 4. 𝑓 (𝑥) =
𝑥−3 4𝑥−1

5. Show that 𝑓(𝑥) = |𝑥 − 1| is not a one-to-one function. Write your solution and
answer at the back.

DBAG: GENERAL MATHEMATICS 11