Documenti di Didattica
Documenti di Professioni
Documenti di Cultura
Geo Ge Bra For Geometry
Caricato da
Dyg NorsheillaTitolo originale
Copyright
Formati disponibili
Condividi questo documento
Condividi o incorpora il documento
Hai trovato utile questo documento?
Questo contenuto è inappropriato?
Segnala questo documentoCopyright:
Formati disponibili
Geo Ge Bra For Geometry
Caricato da
Dyg NorsheillaCopyright:
Formati disponibili
GeoGebra Geometry
Project Maths Development Team 2013 www.projectmaths.ie Page 1 of 24
Index
Activity Topic Page
1 Introduction 4
2 To construct an equilateral triangle 5
3 To construct a parallelogram ABCD, where the length of AB = 5 5
cm, the length of BC=6 cm and the angle ABC is 40
4 To construct an isosceles triangle 7
5 To demonstrate the enlargement of a triangle by the ray method, 8
where the scale factor k is greater than 0
6 Constructing medians and constructing the centroid of a triangle 9
7 Constructing perpendicular bisectors (mediators) and 9
constructing the circumcentre and circumcircle of a triangle
8 Constructing the bisectors of the angles and constructing the 10
incentre and incircle of a triangle
9 To demonstrate reflection in a line 11
10 To demonstrate reflection in a point 11
11 To demonstrate how to use a vector to translate a polygon 12
12 Plotting points with fixed coordinates, reading coordinates, 12
drawing line segments and finding their lengths and midpoints
13 Using the New Point tool to plot points with variable coordinates 13
14 Plotting a line 13
15 To find the points of intersection of a line with the axes 14
16 To find the slope of a line 14
17 Using sliders to see the effect of varying m and c in the equation 15
of the line y=mx+c
18 Drawing triangles, finding area, finding area of the image of a 16
triangle under a translation
19 To demonstrate a circle as a set of points equidistant from a given 17
Project Maths Development Team 2013 www.projectmaths.ie Page 2 of 24
point
20 Plotting a circle given the centre and one point 17
21 Plotting a circle given a centre (0,0) and radius 4 18
22 Use a Slider to vary r and to Investigate equations of the type x2 + 18
y2 = r2
23 Intersection of lines and circles 18
24 To find the equation of the tangent to circle 19
25 Circles whose centres are not at (0,0) 19
26 Transformations of the circle 20
Appendix A 22
A1: How to save a file as a GeoGebra file
A2: How to save a file as an interactive web page
Appendix B 24
B1: To Insert an Image
B2: Check Box to Show / Hide objects
Project Maths Development Team 2013 www.projectmaths.ie Page 3 of 24
Activity 1: Introduction
To download GeoGebra go to www.geogebra.org and the following window will appear.
Click Free Software and the following window will appear.
Click the platform suitable for your computer and follow the indicated steps to download
GeoGebra.
Note: In order to run GeoGebra it is essential that an up to date version of Java is available
on your machine. This package is available at free at http://www.java.com/en/ .
In GeoGebra there are three views, Algebra, Graphics and Spreadsheet. The bar containing
File, Edit etc. is known as the Menu bar and depending if you have the cursor clicked in the
Graphics or the Spreadsheet you get a different toolbar.
Project Maths Development Team 2013 www.projectmaths.ie Page 4 of 24
Graphics
Algebra Spreadsheet
Input Bar
Note: When you click on the Graphics the following toolbar appears:
and when you click on the Spreadsheet the following toolbar appears:
Note: If the Spreadsheet is not visible go to View and click Spreadsheet and if the Graphics
is not visible go to View and choose Graphics.
Activity 2: To construct an equilateral triangle
1. Draw two points A and B using the New Point tool
.
2. Draw the line segment AB using the Segment between
Two Points tool .
3. From A draw a circle through B using the Circle with Centre through a Point tool
4. From B draw a circle through A using the Circle with Centre through a Point tool
5. Find one intersection C of the two circles using the Intersect Two Objects tool .
6. Draw the line segments AC and BC using the Segment between Two Points tool
.
7. Hide the circles by right clicking them and deselecting Show Object.
Project Maths Development Team 2013 www.projectmaths.ie Page 5 of 24
Activity 3: To construct a parallelogram ABCD,
where the length of AB = 5 cm, the length of BC=6
cm and the angle ABC is 40
1. Create the point A using the New Point tool .
2. Select the Segment with Fixed Length from Point tool . Click on A.
In the new dialogue box that appears type in the value 5 and click OK.
3. If the labels have not appeared on the points A and B, right click on these points and
select Show label.
4. Select the Angle with Given Size tool . Click on the point A followed by the point
B. In the new dialogue box that appears, replace the 45 with 40 and check that
clockwise is selected. Click OK.
5. Select the Circle with Centre and Radius tool , click on the point B and in the
new dialogue box insert 6 for the radius. Click OK.
6. Select the Ray through Two Points tool and click on B followed by A.
7. Find the point of intersection C of the ray and the circle using the Intersect Two
Objects tool .
8. Select the Angle with a Given Size tool , click on the point B followed by the
point A. In the new dialogue box that appears, insert 140 and check that
anticlockwise is selected. Click OK.
9. Select the Circle with Centre and Radius tool , click the point A and in the new
dialogue box insert 6 for the radius. Click OK.
10. Select the Ray through Two Points tool and click on A followed by B.
11. Find the point of intersection D of the ray and the circle formed in No 9 and No 10.
12. Create the line segment DC using the Segment between Two Points tool .
13. Hide unnecessary objects by right clicking them and deselecting Show Object. Draw
line segments as required to give the parallelogram ABCD.
Project Maths Development Team 2013 www.projectmaths.ie Page 6 of 24
Activity 4: To construct an isosceles triangle
1. Select the tool (Circle with Centre through a Point) and construct a circle
centre A through point B. If the labels are not showing, right click, select Properties
and with the Basic tab open, click on Show Label.
2. Select the Point on Object tool and construct any point C on the
circumference of circle c.
3. Select the Segment between Two Points tool and construct [AC]
4. Construct [BC] and [AB].
5. Right click on one side of the triangle, select Properties, and with the Basic tab open,
click on the drop down arrow beside the Show Label
box. Select Name and Value to show the name and
length of this side of the triangle. Repeat for the
other triangle sides.
6. Drag each vertex of triangle ABC and note the length
of its sides.
7. Hide the circle, by right clicking on it and clicking on
Show Object.
8. Measure the 3 angles in the triangle using the Angle
tool .
9. Drag any of the vertices of the triangle ABC and observe how the angle measures
change.
Project Maths Development Team 2013 www.projectmaths.ie Page 7 of 24
Activity 5: To demonstrate the enlargement of a triangle by the ray
method, where the scale factor k is greater than 0
1. Create the polygon ABC in the shape of a small triangle using the Polygon tool .
Note: If A is for example the first point of the polygon, then A must be the last point
clicked again at the end.
2. Create the point D using the New Point tool , to the left of A.
3. Using the Ray through Two Points tool draw rays through DA, DB and DC.
4. Create a slider called g with min value 0, max 5 and increment 0.1.
Note: To create a slider: Go to the Slider tool and click on the screen, where you
want your slider located. Choose if you want it to be a Number, Angle or Integer.
Give it a name. Choose the Min, Max values and the Increment you want it to go up
in. Click Apply.
5. Set the slider to 2.
6. Select the Enlarge Object from Point by Factor tool . Click on the polygon that
forms the triangle. Click on point D and in the new dialogue box that appears type in
the name of the slider (g in this case) and click OK.
7. Move the original polygon to enable the enlargement to be demonstrated clearly.
Project Maths Development Team 2013 www.projectmaths.ie Page 8 of 24
Activity 6: Constructing medians and constructing the centroid of a
triangle
(A median is a line segment connecting any vertex of a triangle to the midpoint of the opposite side)
1. Click on File and select New Window.
2. Draw a triangle using Polygon tool as above.
3. Using the Midpoint or Centre tool and the Line Segment tool , construct
the three medians of the triangle.
4. Construct the intersection of the medians by selecting the Intersect Two Objects tool
.
5. Drag any of the vertices of the triangle and note that the 3 medians remain
concurrent, at the centroid.
Activity 7: Constructing perpendicular bisectors (mediators) and
constructing the circumcentre and circumcircle of a
triangle
1. Click on File, New Window, and draw a triangle using the Polygon tool as above.
2. Select Midpoint or Centre tool and selecting each side of the triangle in turn,
construct the midpoints of each side.
3. Using the Perpendicular Bisector tool, select each side to construct
perpendicular bisectors (mediators) of each side.
4. Select the Intersect Two Objects tool and then 2 of the perpendicular bisectors
to construct the circumcentre.
5. The equations of the 3 perpendicular bisectors are shown in the Algebra window.
6. Hide the perpendicular bisectors by right clicking on each one and clicking on Show
Object. Drag the vertices to see the circumcentre change position.
Project Maths Development Team 2013 www.projectmaths.ie Page 9 of 24
7. Using the Circle through a Point tool , then the circumcentre D and one of the
vertices of the triangle and construct the circumcircle. This passes through the 3
vertices.
8. Drag the vertices of the triangle to confirm the construction.
Activity 8: Constructing the bisectors of the angles and constructing
the incentre and incircle of a triangle.
1. Using the Polygon tool construct a triangle ABC in a new window. Select ,
the Angle Bisector tool. Select the points B, A and C, in that order, to construct the
angular bisector of BAC. Repeat for the other two angles in the triangle.
2. Select the Intersect Two Objects tool and 2 of the angle bisectors to construct
the incentre.
3. Hide the angle bisector lines.
4. Selecting the Perpendicular Line tool, draw a perpendicular line from the
incentre D, to line AB or any of the 3 sides of the triangle. With the Intersect Two
Objects tool selected construct the intersection E of side AB and this
perpendicular line.
Project Maths Development Team 2013 www.projectmaths.ie Page 10 of 24
5. Hide the perpendicular line. Select , and with D as centre and E as the point
on the circle, construct the incircle using the Circle with Centre through a Point tool
6. Drag the vertices to confirm the construction.
Activity 9: To demonstrate reflection in a line
1. Create a polygon using the Polygon tool and a line using the Line Through
Two Points tool , if using a line other than the X or Y axis.
2. Go to the Reflect Object in Line tool and click on the polygon plus the line or
the X or Y axis whichever is being used.
3. Now drag the line and or the polygon to different locations and see the image
change accordingly.
Activity 10: To demonstrate reflection in a point
1. Create a polygon using the Polygon tool and a point using the New Point tool.
Click on the Reflect Object in point tool and click on the polygon and the point.
2. Now drag the point and the polygon to different locations etc. and see the image
change accordingly.
Project Maths Development Team 2013 www.projectmaths.ie Page 11 of 24
Activity 11: To demonstrate how to use a vector to translate a
polygon
1. Create a polygon using the Polygon tool and create the vector that you wish to
use for the translation using the Vector from Point tool .
2. Go to the Translate Object by Vector tool and click on the polygon, followed by
the vector. Both the vector and the polygon can be changed and see how the image
changes accordingly.
Activity 12: Plotting points with fixed coordinates, reading
coordinates, drawing line segments and finding their lengths and
midpoints
Enter the point (2, 5), on the Input Bar, and press Enter on the keyboard.
The coordinates of points are displayed in the Algebra window, once Enter is pressed.
Plot the point (-1, 2), displaying its coordinates on the Graphics.
To display the coordinates on the Graphics: Right click on the point, select Object Properties,
and with the Basic tab open, and the box Show Label ticked, choose Name and Value
from the drop down arrow beside it.
Project Maths Development Team 2013 www.projectmaths.ie Page 12 of 24
Select the Segment between Two Points tool and then select points A and B to plot
segment [AB].
The length of line segment [AB] i.e. |AB|, is displayed in the Algebra window as a=
(To display the length of a line segment, right click on it, choose Object Properties and with
the Basic tab open, and the box Show Label ticked, choose Name and Value from the
drop down arrow beside it.)
Select the Midpoint tool, . Then select the line segment [AB] or points A and B to get
the midpoint, which is plotted and the coordinates are displayed in the Algebra window.
Activity 13: Using the New Point tool to plot points with
variable co-ordinates
With the New Point tool selected and clicking anywhere on the Graphics View, points
may be plotted whose coordinates are displayed automatically in the Algebra window.
Dragging these points changes the co-ordinates.
Activity 14: Plotting a line
In the Input Bar type in 2x-3y+5=0. In the Algebra window it will be written as -2x+3y=5.
Right click on the line and select Object Properties, and
choose Name and Value, to have the equation appear in
the Graphics (View).
Project Maths Development Team 2013 www.projectmaths.ie Page 13 of 24
Activity 15: To find the points of intersection of a line with the axes
1. Draw a line a using the Line through Points tool .
2. Using the Intersect Two Objects tool , select the line a and the axis. The point of
intersection A is marked on the line and its co-ordinates are displayed in the Algebra
window.
3. Repeat this for the point of intersection with the axis.
Activity 16: To find the slope of a line
1. Draw a line using the Line between Two Points tool .
2. Select the Slope tool and click on the line, to find its slope.
The value of the slope is displayed in the Algebra window.
Project Maths Development Team 2013 www.projectmaths.ie Page 14 of 24
Activity 17: Using sliders to see the effect of varying m and c in the
equation of the line y=mx+c
1. Go to File and select New Window.
2. Go to the Slider tool and click on the screen, where you want your slider located.
3. Choose Number rather than Angle. Give the slider a name m. Choose the min, max
values and the increment you want it to go up in. Click Apply.
4. Go to the Slider tool and click on the screen, where you want your slider located.
5. Choose Number rather than Angle. Give the slider a name c. Choose the min, max
values and the increment you want it to go up in. Click Apply.
6. Type in y=mx+c into the Input Bar. Vary the value of m by selecting , and
dragging the slider m. Observe the effect.
7. Investigate the effects of varying c by dragging c along the slider.
8. What do you conclude about m and c?
To change the sliders
Right click on slider m. Select Object Properties and the Slider tab to vary max and min
values, the increment, and the width of the line representing the slider. Selecting the
Colour tab allows you to vary the colour of the slider. The Style tab allows you to vary
the thickness of the slider. Select the X at the top of the dialogue box when finished.
Project Maths Development Team 2013 www.projectmaths.ie Page 15 of 24
Activity 18: Drawing triangles, finding area, finding area of the
image of a triangle under a translation
Triangles may be plotted using the New point tool or by typing in specific co-ordinates
in the Input line and joining the points with line segments or else by using the Polygon tool.
Use the Polygon tool to make a triangle ABC. The area is given in the Algebra window
as poly = or alternatively you may click on Command on the Input Bar, select the word Area
which will be followed by closed square brackets i.e. Area[]. Inside the brackets type A,B,C
and the area is printed in the Algebra window as d= .
Using the instructions (How to use a vector to translate a polygon), translate the triangle
under the defined translation. Drag the points of the original triangle and note the area of
the original triangle and its image. The area of both triangles will be displayed in the Algebra
window as Poly 1 = and Poly 1 =.
Project Maths Development Team 2013 www.projectmaths.ie Page 16 of 24
Activity 19: To demonstrate a circle as a set of points equidistant
from a given point
1. Plot the point (1, 2) by typing (1, 2) in the Input Bar and pressing Enter on the
keyboard.
2. Display its co-ordinates on the Graphics right click the point, select Object
Properties and with the Basic tab open click the box beside Show Label and choose
Name and Value.
3. Select the Segment with Fixed Length tool .
4. Click on the point A and type 4 in for length in the dialogue box which appears.
5. Click OK.
6. Point B is drawn 4 units away from A. Right click on point B and select Properties,
Show Trace.
7. Drag B and observe.
8. Select View on the menu bar, then Refresh views to get rid of the traces.
Activity 20: Plotting a circle given the centre and one point
1. Plot points A(0,0) and B(-1,2)
2. Select and the 2 points A and B and draw a circle
The equation of the circle is displayed in the Algebra window.
The cirlce is also displayed on the Graphics.
Project Maths Development Team 2013 www.projectmaths.ie Page 17 of 24
Activity 21: Plotting a circle given a centre (0,0) and radius 4
1. In the Input Bar type (0,0) and press Enter on the keyboard.
2. Select Circle with Centre and Radius tool .
3. Type in 4 into the dialogue box which appears and click on Apply.
Activity 22: Use a slider to vary r and to investigate equations of
the type x2 + y2 = r2
1. Select the slider tool and click on the Graphics.
2. Type in r for the slider name, 0 for Min: and 6 for the Max: and 1 for the Increment:.
3. Type in x^2+y^2=r^2 into the Input Bar and press Enter on the keyboard.
4. Drag the slider to vary the value of r.
Activity 23: Intersection of lines and circles
1. To plot the circle type x^2+y^2=10 in the Input Bar and press Enter on the keyboard.
2. To plot the line type 3x+y+10=0 in the Input Bar and press Enter on the keyboard.
3. Using the Intersect two Objects tool find where the circle and line meet and
make a conclusion about the relationship between the line and the circle.
Project Maths Development Team 2013 www.projectmaths.ie Page 18 of 24
Activity 24: To find the equation of the tangent to circle
1. Type x2 + y2 = 8 into the Input Bar and press Enter on the keyboard to plot the circle,
called c.
2. In the Input Bar type (2,2) and press Enter on the keyboard to create a point called A.
3. In the Input Bar type Tangent[A,c]
The tangent to the circle is then drawn and its equation is displayed in the Algebra
window.
Activity 25: Circles whose centres are not at (0,0)
To create the circle with centre at (2,1) and radius equal to 4.
1. Enter (2,1) in the Input Bar and press Enter on the keyboard.
2. Select the Circle with Centre and Radius tool .
3. Type 4 in the new dialogue box that appears and press OK.
4. Right click on the circle and choose Object Properties and with the Basic tab open click
Show Label and from the drop down menu choose Name and Value.
Plot the following circles and note their equations:
(i) Centre (1,3) Radius 2
(ii) Centre (5,-1) Radius 3
(iii) Centre (-3,1) Radius 5 (typed in as sqrt(5))
Project Maths Development Team 2013 www.projectmaths.ie Page 19 of 24
To draw a circle with centre (h,k) and radius r, where h, k and r can vary?
Set up sliders for h, k, and r and investigate the equations of circles with different values of
h, k and r, typing in (x-h)^2+(y-k)^2 =r^2 in the input Bar and pressing Enter on the
keyboard.
What is the effect of varying h?
What is the effect of varying k?
To display the circle equation in the form x2 y 2 2 gx 2 fy c , right click on the circle
equation in the Algebra window and click on the option
ax2 bxy cy 2 dx ey f
Activity 26: Transformations of the circle
1. Plot the circle x2 y 2 4 x 6 y 4 0 .
2. The equation will automatically be displayed in the Algebra window in the form
( x h)2 ( y k )2 r 2 . By right clicking on the equation it is possible to toggle back
and forth between the two forms of the equation.
Transformations of the circle using Axial Symmetry
Select the Reflect Object in a Line tool and find the image of the circle under axial
symmetry in the x axis. Compare the equations of the circle and its image.
Transformations of the circle using Central Symmetry
Plot the point (0,0).
Select the Reflect Object in a Line and find the image of the circle by central symmetry in
the origin. Compare the equations of the circle and its image.
Project Maths Development Team 2013 www.projectmaths.ie Page 20 of 24
Transformations of the circle using a Translation
Plot the points (-2,1) and (5,3).
Select the Vector between Two Points tool , and select each of the points (-2,1) and
(5,3) to define the translation (-2,1) to (5,3).
Select Translate Object by Vector , followed by the circle and the vector to translate
the circle. Compare the equations of the circle and its image.
Note: When displaying circles it is important that the ratio of the xAxis: yAxis is 1:1.
This is achieved by right clicking on the Graphics and selecting Graphics. A new dialogue box
appears.
With the Basic tab open change the ratio of the xAxis to yAxis to 1:1.
The xMin, xMax, yMin and yMax values can now be changed to show the circle and its
image if the Graphics window is not displaying both.
Click the X at the top of the dialogue box.
The Move Graphics View, Zoom In and Zoom Out tools can also be used.
Project Maths Development Team 2013 www.projectmaths.ie Page 21 of 24
Appendix A
A1: How to save a file as a GeoGebra file
1. Go to the Menu and choose Save as from the drop down menu. A new dialogue box
appears.
2. For Save in, navigate to the folder that you wish the file to be saved in.
3. For File name select the name you wish to give your file.
4. Click Save. A file with the .ggb extension is created. This extension identifies the file
as a GeoGebra file and it can be opened again and adjustments made using the
GeoGebra application.
A2: How to save a file as an interactive web page
1. First save your file as a GeoGebra file.
2. Go to File, from the drop down menu select Export and from the further menu select
the option Export Dynamic Worksheet as Webpage (html). A new dialogue box
appears.
Project Maths Development Team 2013 www.projectmaths.ie Page 22 of 24
3. Click on the Export as Webpage tab.
4. Add Title, Author, etc. Then click on the Advanced tab and a new dialogue box
appears.
It is recommended that one clicks the Show Icon to reset construction button.
5. Click Export.
6. Navigate to the folder you want to save your file in. Give it the name of your choice.
Note: This file will have a .html extension and will be viewed using an Internet
browser such as Internet Explorer 8.
7. Click Save and your default Internet browser will open.
8. When the webpage comes up you the following message will normally appear at the
top of the screen.
9. Click on Click here for options and choose Allow Blocked Content... and click Yes.
Project Maths Development Team 2013 www.projectmaths.ie Page 23 of 24
Appendix B
B1: To insert an image: Go to Insert Image tool and click at the location on the
Graphics where you want to place the image. A new box appears. Select your picture and
click Open. Be careful as a lot of pictures are too big and will need to be edited to the size
you require using alternative software.
B2: Check Box to Show / Hide objects: Click on the Check Box to Show / Hide Objects
and click on the Graphics at the location you require the check box to appear. In the
new dialogue box that appears, type in your Caption for example Click to hide or show the
circle. Follow the arrow under Select objects in construction or choose from list in the
dialogue box and in this case choose the circle. You can select more than one object here.
Click Apply. With the Selection arrow clicked, click the check box and the circle disappears.
Project Maths Development Team 2013 www.projectmaths.ie Page 24 of 24
Potrebbero piacerti anche
- Konica Minolta Regius CS-3 Installation and Service ManualDocumento637 pagineKonica Minolta Regius CS-3 Installation and Service ManualKirje Martinez Yo0% (1)
- CATIA V5-6R2015 Basics - Part II: Part ModelingDa EverandCATIA V5-6R2015 Basics - Part II: Part ModelingValutazione: 4.5 su 5 stelle4.5/5 (3)
- Parallel Architecture ClassificationDocumento41 pagineParallel Architecture ClassificationAbhishek singh0% (1)
- Information SecurityDocumento2 pagineInformation SecurityRaghunath ParulekarNessuna valutazione finora
- Geogebra TutorialDocumento9 pagineGeogebra TutorialIsmail HashimNessuna valutazione finora
- Planar Linkage Analysis Using GeogebraDocumento26 paginePlanar Linkage Analysis Using GeogebraEvan AV100% (1)
- Corel Draw TutorialDocumento33 pagineCorel Draw TutorialMohit Saras100% (1)
- Practical - 7: Draw Different Graphical Shapes in AutocadDocumento3 paginePractical - 7: Draw Different Graphical Shapes in AutocadRabia RindNessuna valutazione finora
- Tutorial 2: Particles Convected With The Flow Along A Curved PipeDocumento29 pagineTutorial 2: Particles Convected With The Flow Along A Curved PipeAdriko NormanNessuna valutazione finora
- Bac Bac: AGC CGB BGA AFG CEG BDGDocumento3 pagineBac Bac: AGC CGB BGA AFG CEG BDGHuyenThanhNguyenNessuna valutazione finora
- Geometers SketchpadDocumento5 pagineGeometers SketchpadEnder EkerNessuna valutazione finora
- Modul SW EnglishDocumento15 pagineModul SW EnglishrezaardNessuna valutazione finora
- Geometer's Sketchpad Fractals PresentationDocumento18 pagineGeometer's Sketchpad Fractals PresentationSyahmi StriverNessuna valutazione finora
- Workbook6 Tutorial GeogebraDocumento9 pagineWorkbook6 Tutorial GeogebraHarunAbdulRohmanNessuna valutazione finora
- Pfc3d-Ccfd Tutorial 1Documento20 paginePfc3d-Ccfd Tutorial 1DINNessuna valutazione finora
- SBS - L4-03 Defining Sketch DimensionsDocumento6 pagineSBS - L4-03 Defining Sketch DimensionsDavid BernalNessuna valutazione finora
- Introduction To Solidworks: 1. Creating A New Part FileDocumento3 pagineIntroduction To Solidworks: 1. Creating A New Part FileDr. Ir. R. Didin Kusdian, MT.Nessuna valutazione finora
- Demo KaleidoscopeDocumento3 pagineDemo KaleidoscopeTracy Lloyd MaaghopNessuna valutazione finora
- ME 210 Mechanical Engineering Drawing & Graphics: College of Engineering SciencesDocumento8 pagineME 210 Mechanical Engineering Drawing & Graphics: College of Engineering SciencesEbrahim HanashNessuna valutazione finora
- Unit19 RESULTS INTERPRETATION AND DISCUSSIONDocumento15 pagineUnit19 RESULTS INTERPRETATION AND DISCUSSIONkatyaNessuna valutazione finora
- Procedure For Drafting Using Solid EdgeDocumento3 pagineProcedure For Drafting Using Solid EdgeKailas Sree ChandranNessuna valutazione finora
- Workbook2 Tutorial GeogebraDocumento8 pagineWorkbook2 Tutorial GeogebraHarunAbdulRohmanNessuna valutazione finora
- HairbrushDocumento26 pagineHairbrushJuan Manuel Arguello EspinosaNessuna valutazione finora
- Sub-Module of Basic Drawing & Cad: Universiti Teknikal Malaysia Melaka Fakulti Kejuruteraan PembuatanDocumento20 pagineSub-Module of Basic Drawing & Cad: Universiti Teknikal Malaysia Melaka Fakulti Kejuruteraan Pembuatanstamford_bridgeNessuna valutazione finora
- CAD Handout - Cambridge UniversityDocumento16 pagineCAD Handout - Cambridge UniversityVictor FizesanNessuna valutazione finora
- Mill Lesson 9 SampleDocumento23 pagineMill Lesson 9 SamplefbienpeNessuna valutazione finora
- Lab Report 12: ObjectiveDocumento10 pagineLab Report 12: ObjectiveMUHAMMAD AbdullahNessuna valutazione finora
- Lecture 10Documento25 pagineLecture 10S AhmedNessuna valutazione finora
- © Project Maths Development Team 2009Documento22 pagine© Project Maths Development Team 2009Ismail HashimNessuna valutazione finora
- Truongmill Lesson 13Documento34 pagineTruongmill Lesson 13TruonglanaNessuna valutazione finora
- Geo Ge Bra For FunctionsDocumento37 pagineGeo Ge Bra For FunctionsMarcos NascimentoNessuna valutazione finora
- MasterCam Sample-Mill-Lesson-9Documento17 pagineMasterCam Sample-Mill-Lesson-9pptmnlt100% (3)
- Bac Bac: AGC CGB BGA AFG CEG BDGDocumento3 pagineBac Bac: AGC CGB BGA AFG CEG BDGHuyenThanhNguyenNessuna valutazione finora
- Sketchup Basics PDFDocumento27 pagineSketchup Basics PDFsrk bhaiNessuna valutazione finora
- Idiot's Guide To Basic Sketchup Functions PDFDocumento27 pagineIdiot's Guide To Basic Sketchup Functions PDFShaneNessuna valutazione finora
- Lab Manual: Cad 3DDocumento25 pagineLab Manual: Cad 3DnaveenNessuna valutazione finora
- 3D Wing Tutorial: PurposeDocumento38 pagine3D Wing Tutorial: PurposePrabhakar Gidda100% (1)
- 3 Square Root SpiralDocumento2 pagine3 Square Root SpiralSawarSagwalNessuna valutazione finora
- Lab Activity #3Documento15 pagineLab Activity #3JULLEEN ANN MARIE CONVENTONessuna valutazione finora
- Solids Lesson 4Documento32 pagineSolids Lesson 4camb2270Nessuna valutazione finora
- COM 215 Computer Packages II Practical BookDocumento18 pagineCOM 215 Computer Packages II Practical Bookabdulqudus abdulakeemNessuna valutazione finora
- How To Develop A ConeDocumento11 pagineHow To Develop A ConeEby100% (1)
- Mill Lesson 5 PDFDocumento57 pagineMill Lesson 5 PDFFadhilGhazyNessuna valutazione finora
- Ej Create PartsDocumento24 pagineEj Create PartsNOCHE3Nessuna valutazione finora
- 14 2.5D Solids TutorialDocumento40 pagine14 2.5D Solids TutorialrodrigodelacalperezNessuna valutazione finora
- Geogebra Quickstart en DesktopDocumento10 pagineGeogebra Quickstart en DesktopIldeberto de los SantosNessuna valutazione finora
- L3-01-Creating The Tire SketchDocumento6 pagineL3-01-Creating The Tire Sketchram rakNessuna valutazione finora
- 1 Tour 8-SnowflakeDocumento7 pagine1 Tour 8-SnowflakeZara ZarithNessuna valutazione finora
- MAE 477/577 - Spring 2016 CAD Applications: CategoryDocumento22 pagineMAE 477/577 - Spring 2016 CAD Applications: CategoryZurina MANessuna valutazione finora
- Geometer's Sketchpad: Universiti Brunei DarussalamDocumento9 pagineGeometer's Sketchpad: Universiti Brunei Darussalamyul812Nessuna valutazione finora
- Sketch UpDocumento19 pagineSketch UpAlain Mel R. CresciniNessuna valutazione finora
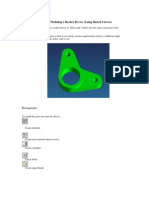
- Project 5: Modeling A Rocker Device (Using Sketch Curves) : PrerequisitesDocumento20 pagineProject 5: Modeling A Rocker Device (Using Sketch Curves) : PrerequisitessamihakhanNessuna valutazione finora
- Sketchup Instructions: Every Architect Needs To Know How To Use Sketchup!Documento27 pagineSketchup Instructions: Every Architect Needs To Know How To Use Sketchup!Miguel Alfonso M. MurilloNessuna valutazione finora
- Mcq-On Catia: 1. What Is The Colour of Under-Constrained Elements in CATIA SketcherDocumento15 pagineMcq-On Catia: 1. What Is The Colour of Under-Constrained Elements in CATIA SketcherRupesh Kamat100% (1)
- NX 9 for Beginners - Part 2 (Extrude and Revolve Features, Placed Features, and Patterned Geometry)Da EverandNX 9 for Beginners - Part 2 (Extrude and Revolve Features, Placed Features, and Patterned Geometry)Nessuna valutazione finora
- SketchUp for Site Design: A Guide to Modeling Site Plans, Terrain, and ArchitectureDa EverandSketchUp for Site Design: A Guide to Modeling Site Plans, Terrain, and ArchitectureNessuna valutazione finora
- Autodesk 3ds Max 2014 Essentials: Autodesk Official PressDa EverandAutodesk 3ds Max 2014 Essentials: Autodesk Official PressNessuna valutazione finora
- Assessment Questionnaire SXEP 3207 2017/2018 (1) : NAMEDocumento2 pagineAssessment Questionnaire SXEP 3207 2017/2018 (1) : NAMEDyg NorsheillaNessuna valutazione finora
- MathorqDocumento85 pagineMathorqPaul TurnerNessuna valutazione finora
- Monsta XDocumento4 pagineMonsta XDyg NorsheillaNessuna valutazione finora
- Subspace Test Strategy: We Want To See If H Is A Subspace of VDocumento7 pagineSubspace Test Strategy: We Want To See If H Is A Subspace of VDyg NorsheillaNessuna valutazione finora
- Derived From: WWW - Niu.edu/facdevDocumento3 pagineDerived From: WWW - Niu.edu/facdevDyg NorsheillaNessuna valutazione finora
- Smes1204 Sxep1101 Sxep1102 Paet3101 Ppex2101 Sxep2107 Sxep2105 Ppet3104Documento11 pagineSmes1204 Sxep1101 Sxep1102 Paet3101 Ppex2101 Sxep2107 Sxep2105 Ppet3104Dyg NorsheillaNessuna valutazione finora
- Introduction GeogebraDocumento10 pagineIntroduction GeogebraDyg NorsheillaNessuna valutazione finora
- 1 Introduction To LP: F (X) S.T. X SDocumento7 pagine1 Introduction To LP: F (X) S.T. X SDyg NorsheillaNessuna valutazione finora
- Write Your Comments About Education in FinlandDocumento1 paginaWrite Your Comments About Education in FinlandDyg NorsheillaNessuna valutazione finora
- Know Your Aptitude For Class-5 PDFDocumento82 pagineKnow Your Aptitude For Class-5 PDFRakeshRanjan100% (1)
- Business To Manufacturing Markup Language Batch Information Version 6.0 - March 2013 Batchml - Batch InformationDocumento52 pagineBusiness To Manufacturing Markup Language Batch Information Version 6.0 - March 2013 Batchml - Batch InformationWass GharbiNessuna valutazione finora
- A Comprehensive Guide To OT SecurityDocumento18 pagineA Comprehensive Guide To OT SecurityJuan Carlos CortinasNessuna valutazione finora
- JD-800 Model Expansion Owner's Manual: 01 © 2021 Roland CorporationDocumento20 pagineJD-800 Model Expansion Owner's Manual: 01 © 2021 Roland CorporationNicolas TilleNessuna valutazione finora
- Himax: Analog Output Module ManualDocumento52 pagineHimax: Analog Output Module ManualRoberto FinaNessuna valutazione finora
- CambalacheDocumento21 pagineCambalacheRODRINessuna valutazione finora
- IBM System Storage DS3950 Storage Subsystem Injstallation, Users's and Maintenance GuideDocumento252 pagineIBM System Storage DS3950 Storage Subsystem Injstallation, Users's and Maintenance GuideAntonio A. BonitaNessuna valutazione finora
- User Manual (CSCOperator) - REV-202 Destitute Widow Pension Scheme (DWPS)Documento24 pagineUser Manual (CSCOperator) - REV-202 Destitute Widow Pension Scheme (DWPS)DHILIPKUMAR KSNessuna valutazione finora
- WD Elements Play Manual EngDocumento73 pagineWD Elements Play Manual EngAndrey VojdNessuna valutazione finora
- Tonehammer: All Rights Reserved © Tonehammer 2006 - 2010Documento20 pagineTonehammer: All Rights Reserved © Tonehammer 2006 - 2010Nils Van der PlanckenNessuna valutazione finora
- Satellite A215-S5818 PDFDocumento3 pagineSatellite A215-S5818 PDFviewwareNessuna valutazione finora
- Apache Ofbiz Auto Startup Scripts.Documento2 pagineApache Ofbiz Auto Startup Scripts.hillol001Nessuna valutazione finora
- CSC126 Fundamentals of Algorithms & Computer Problem Solving Quiz 1Documento5 pagineCSC126 Fundamentals of Algorithms & Computer Problem Solving Quiz 1muhammad safuanNessuna valutazione finora
- Using Data Analytics To Ask and Answer Accounting Questions: A Look at This ChapterDocumento58 pagineUsing Data Analytics To Ask and Answer Accounting Questions: A Look at This Chaptersalsabila.rafy-2021Nessuna valutazione finora
- 3D Wind Loading TheoryDocumento24 pagine3D Wind Loading TheoryNikola Miletic100% (1)
- Manual LapSim 2013 enDocumento68 pagineManual LapSim 2013 enShefin ShukkoorNessuna valutazione finora
- Second Edition - IIoT DictionaryDocumento12 pagineSecond Edition - IIoT DictionaryricardoNessuna valutazione finora
- Aztech WL556E Wireless Repeater Setup GuideDocumento34 pagineAztech WL556E Wireless Repeater Setup GuideRobert WeeNessuna valutazione finora
- Mchpfsusb Library HelpDocumento883 pagineMchpfsusb Library Helpgem1144aaNessuna valutazione finora
- Logcat Prev CSC LogDocumento59 pagineLogcat Prev CSC LogIonut CaponeNessuna valutazione finora
- Delete Blank Rows in Excel - Easy Excel TutorialDocumento5 pagineDelete Blank Rows in Excel - Easy Excel TutorialJamalodeen MohammadNessuna valutazione finora
- PSPWMDocumento29 paginePSPWMSrinivas SirimullaNessuna valutazione finora
- VEP-A00-P - VEP With LEDs 4 PipesDocumento1 paginaVEP-A00-P - VEP With LEDs 4 PipesNicu NicuNessuna valutazione finora
- ICONICS Suite Resolved Issues 1097Documento19 pagineICONICS Suite Resolved Issues 1097Hồ PhiNessuna valutazione finora
- Manual Multi-Node Patching of Grid Infrastructure and Rac DB Environment Using OpatchautoDocumento7 pagineManual Multi-Node Patching of Grid Infrastructure and Rac DB Environment Using OpatchautoAriel Pacheco RinconNessuna valutazione finora
- Trend Function - TBDocumento35 pagineTrend Function - TBbmw316100% (1)
- Step-By-Step - Migrating Active Directory FSMO Roles From Windows Server 2012 R2 To 2016 - CANITPRODocumento16 pagineStep-By-Step - Migrating Active Directory FSMO Roles From Windows Server 2012 R2 To 2016 - CANITPRODani Kirky YlaganNessuna valutazione finora