Documenti di Didattica
Documenti di Professioni
Documenti di Cultura
Operation Research Note Sheet
Caricato da
Anup Mohapatra0 valutazioniIl 0% ha trovato utile questo documento (0 voti)
39 visualizzazioni1 paginaOperation Research Note Sheet
Copyright
© © All Rights Reserved
Formati disponibili
DOCX, PDF, TXT o leggi online da Scribd
Condividi questo documento
Condividi o incorpora il documento
Hai trovato utile questo documento?
Questo contenuto è inappropriato?
Segnala questo documentoOperation Research Note Sheet
Copyright:
© All Rights Reserved
Formati disponibili
Scarica in formato DOCX, PDF, TXT o leggi online su Scribd
0 valutazioniIl 0% ha trovato utile questo documento (0 voti)
39 visualizzazioni1 paginaOperation Research Note Sheet
Caricato da
Anup MohapatraOperation Research Note Sheet
Copyright:
© All Rights Reserved
Formati disponibili
Scarica in formato DOCX, PDF, TXT o leggi online su Scribd
Sei sulla pagina 1di 1
Notes Sheet for Mid Term Examination (QM2)
30 Nov 2016
Rule 1
Rule 2
Rule 3
Rule 4
Rule 5
Rule 6
Rule 7
Rule 8
Rule 9
# of Variables in (D) = # of Constraints in (P)
# of Constraints in (D) = # of Variables in (P)
Coefficients of Obj. Fn. In (D) comes from r.h.s. of constraints in (P)
If (P) is a max model, then (D) is a min model. If (P) is a min model,
then (D) is a max model
Coefficients in the ith constraint function in (D) are the coefficients
of the ith variable of constraints in (P)
The r.h.ss of constraints in (D) come from the objective function
coefficients in (P)
The sense of the ith constraint in (D) is = iff the ith variable in (P)
is unrestricted
If (P) is a MAX problem, then the constraints in (D) have the same
sense as the corresponding variables in (P). If (P) is a MIN problem,
then the dual constraints have a sense opposite to the
corresponding variable in the original problem
The ith variable in (D) is unconstrained iff the ith constraint in (P) is
an equality
If (P) is a MAX problem, then the variables in (D) have sense
opposite to the sign of the corresponding constraints in (P). If (P) is
a MIN problem, then the dual variables have the same sense as the
corresponding constraints in (P)
Weak Duality Theorem
Let X denote a feasible solution to (P), and Y a feasible solution to (D)
If (P) is a MAX problem and (D) a MIN problem, then Obj.Val.(X) <= Obj.Val.(Y)
If (P) is a MIN problem and (D) a MAX problem, then Obj.Val.(X) >= Obj.Val.(Y)
Strong Duality Theorem:
If (P) has a finite optimal solution then (D) also has a finite optimal solution, and
vice versa.
Further, in such a case the optimal objective function values for both problems
are equal.
That is,
O.V.(X*) = O.V.(Y*)
Principle of Complementary Slackness:
At optimality, if ith constraint in (P) is loose, then the corresponding optimal dual
variable Y*i = 0
At optimality, if Y*i > 0, then the corresponding primal constraint is tight.
Potrebbero piacerti anche
- Probability Cheatsheet 140718Documento7 pagineProbability Cheatsheet 140718Mohit Agrawal100% (1)
- Row Game - Multiplying Polynomials and MonomialsDocumento2 pagineRow Game - Multiplying Polynomials and MonomialsLisa Henry100% (1)
- Liquidity Vs SolvencyDocumento44 pagineLiquidity Vs SolvencyAnup Mohapatra100% (1)
- Elementary Properties of Cyclotomic Polynomials by Yimin GeDocumento8 pagineElementary Properties of Cyclotomic Polynomials by Yimin GeGary BlakeNessuna valutazione finora
- Mathematics 9 First Quarter ExamDocumento4 pagineMathematics 9 First Quarter ExamMayang Robete100% (1)
- ISyE/Math/CS/Stat 525 - Linear Optimization AssignmentDocumento9 pagineISyE/Math/CS/Stat 525 - Linear Optimization AssignmentNengke LinNessuna valutazione finora
- Python Data Science Cheat SheetDocumento1 paginaPython Data Science Cheat SheetMaisarah Mohd PauziNessuna valutazione finora
- Modern Bayesian EconometricsDocumento100 pagineModern Bayesian Econometricsseph8765Nessuna valutazione finora
- Mathematics: Quarter 1 - Module 6: Division of Polynomials, Remainder, Factor, and The Rational Root TheoremDocumento22 pagineMathematics: Quarter 1 - Module 6: Division of Polynomials, Remainder, Factor, and The Rational Root TheoremAngela SolivioNessuna valutazione finora
- WINSEM2022-23 BMAT205L TH VL2022230502546 Reference Material I 10-01-2023 Predicate LogicDocumento29 pagineWINSEM2022-23 BMAT205L TH VL2022230502546 Reference Material I 10-01-2023 Predicate LogicIzhanNessuna valutazione finora
- Discrete STR NotesDocumento20 pagineDiscrete STR Noteshas_zindarod8495Nessuna valutazione finora
- Chapter 1 Predicate Sand Quanti FierDocumento29 pagineChapter 1 Predicate Sand Quanti Fiermastura salmanNessuna valutazione finora
- 2Chapter1 P2 Predicate LogicDocumento29 pagine2Chapter1 P2 Predicate Logicknbx7xcm9cNessuna valutazione finora
- Discrete MathematicsDocumento45 pagineDiscrete MathematicsmagisrajNessuna valutazione finora
- AciidsDocumento16 pagineAciidsTuấn Lưu MinhNessuna valutazione finora
- Discrete Mathematics: Propositional LogicDocumento46 pagineDiscrete Mathematics: Propositional LogicSatyanarayana Murthy100% (1)
- Chapter 1 (Part 2) Predicates & QuantifiersDocumento39 pagineChapter 1 (Part 2) Predicates & QuantifiersSahtish Rao RamulooNessuna valutazione finora
- PE1Documento5 paginePE1mca.ambika6100Nessuna valutazione finora
- SAA For JCCDocumento18 pagineSAA For JCCShu-Bo YangNessuna valutazione finora
- Duality in optimization and constraint satisfaction analyzed through inference and relaxation dualsDocumento13 pagineDuality in optimization and constraint satisfaction analyzed through inference and relaxation dualstaulzNessuna valutazione finora
- Discrete Mathematics AND Its ApplicationsDocumento49 pagineDiscrete Mathematics AND Its ApplicationsNguyễn Hoàng TrâmNessuna valutazione finora
- CSE Discrete Math Slide Lecture 03Documento34 pagineCSE Discrete Math Slide Lecture 03MD KhaliNessuna valutazione finora
- Logical Equivalences and QuantifiersDocumento18 pagineLogical Equivalences and QuantifiersВарис ВарисовNessuna valutazione finora
- Predicate LogicDocumento56 paginePredicate LogicDarshini BNessuna valutazione finora
- Solutions To In-Class Problems - Week 8, FriDocumento4 pagineSolutions To In-Class Problems - Week 8, FriRahul PradhanNessuna valutazione finora
- Bi-polynomial rank and determinantal complexity improved lower boundsDocumento20 pagineBi-polynomial rank and determinantal complexity improved lower boundsKunal MittalNessuna valutazione finora
- Chapter 1B Predicate LogicDocumento40 pagineChapter 1B Predicate LogicHabib HasanovNessuna valutazione finora
- Approx Algorithms for Combinatorial Multicriteria OptimizationDocumento26 pagineApprox Algorithms for Combinatorial Multicriteria Optimizationbb_sportsmanNessuna valutazione finora
- Lecture 8-9aDocumento11 pagineLecture 8-9amehtab KhanNessuna valutazione finora
- Conditionals and BiconditionalsDocumento2 pagineConditionals and BiconditionalsElleirbag SerapioNessuna valutazione finora
- Chapter 1 P 2Documento30 pagineChapter 1 P 2EBAADUREHMAN KHANNessuna valutazione finora
- Ped 35602Documento34 paginePed 35602Beket AbayevNessuna valutazione finora
- 18 Predicate Calculus 01 Aug 2020material I 01 Aug 2020 Predicate Calculus IntroductionDocumento9 pagine18 Predicate Calculus 01 Aug 2020material I 01 Aug 2020 Predicate Calculus Introductionkhushboo kanwar rajawatNessuna valutazione finora
- 03 Logic3Documento18 pagine03 Logic3Khalil alrahman MoftahNessuna valutazione finora
- Higher-Order (F, α, β, ρ, d) -Convexity for Multiobjective Programming ProblemDocumento7 pagineHigher-Order (F, α, β, ρ, d) -Convexity for Multiobjective Programming ProbleminventionjournalsNessuna valutazione finora
- Solving Multi Objective Linear Fractional Programming Problem Under Uncertainty Via Robust Optimization ApproachDocumento11 pagineSolving Multi Objective Linear Fractional Programming Problem Under Uncertainty Via Robust Optimization ApproachBasiya KakawlaNessuna valutazione finora
- Irreducible Polynomials That Factor Mod Every Prime: Reed JacobsDocumento23 pagineIrreducible Polynomials That Factor Mod Every Prime: Reed JacobsValentioNessuna valutazione finora
- Predicate LogicDocumento28 paginePredicate LogicgabyssinieNessuna valutazione finora
- QUANTIFIERSDocumento21 pagineQUANTIFIERSGAEA FAYE MORTERANessuna valutazione finora
- Mathematical Foundations of Computer Science LecturesDocumento107 pagineMathematical Foundations of Computer Science LecturesHimanshu YadavNessuna valutazione finora
- Artificial Intelligence 3451: UNIT: 03 Knowledge RepresentationDocumento28 pagineArtificial Intelligence 3451: UNIT: 03 Knowledge RepresentationFarhad Muhammad RiazNessuna valutazione finora
- Numerical Methods: Session 1: Principles of Numerical MathematicsDocumento24 pagineNumerical Methods: Session 1: Principles of Numerical MathematicsDoris riverosNessuna valutazione finora
- Chapter1p2 Predicate Logic PDFDocumento57 pagineChapter1p2 Predicate Logic PDFSagar Sagar100% (1)
- UNIT I-Part-2Documento38 pagineUNIT I-Part-2Suyog JadhavNessuna valutazione finora
- Lecture Notes 02, Predicates and QuantifiersDocumento60 pagineLecture Notes 02, Predicates and Quantifiersqny8n272y7Nessuna valutazione finora
- Discrete Structures: Foundations of Logic and Discrete MathDocumento19 pagineDiscrete Structures: Foundations of Logic and Discrete MathShoaib KareemNessuna valutazione finora
- Discrete Mathematics FoundationsDocumento40 pagineDiscrete Mathematics FoundationsNguyen Hai Ha (K17 HCM)Nessuna valutazione finora
- FOPLDocumento31 pagineFOPLmanicheeseNessuna valutazione finora
- Journal of Statistical Software: More On Multidimensional Scaling and Unfolding in R: Smacof Version 2Documento47 pagineJournal of Statistical Software: More On Multidimensional Scaling and Unfolding in R: Smacof Version 2almirantebenbowNessuna valutazione finora
- Chapter1 - Part2 - LogicDocumento42 pagineChapter1 - Part2 - LogicliasakinahNessuna valutazione finora
- Discrete Mathematics FoundationsDocumento40 pagineDiscrete Mathematics FoundationsNguyen Hai An (K15 HL)Nessuna valutazione finora
- L9 Strong DualityDocumento71 pagineL9 Strong DualityHéctor F BonillaNessuna valutazione finora
- A Bayesian Perspective On Generalization and Stochastic Gradient DescentDocumento4 pagineA Bayesian Perspective On Generalization and Stochastic Gradient DescentRahul MishraNessuna valutazione finora
- Kullback DivDocumento6 pagineKullback DivGuillaume GarnierNessuna valutazione finora
- IGNOU MEC-003 Free Solved Assignment 2012Documento10 pagineIGNOU MEC-003 Free Solved Assignment 2012manuraj4100% (2)
- EE 561 Communication Theory Spring 2003Documento27 pagineEE 561 Communication Theory Spring 2003Mohamed Ziad AlezzoNessuna valutazione finora
- Chapter 1, Part II: Predicate Logic: With Question/Answer AnimationsDocumento21 pagineChapter 1, Part II: Predicate Logic: With Question/Answer Animationshsafs fdassNessuna valutazione finora
- Midterm Review: STAT 5301/MATH 5310 Key ConceptsDocumento6 pagineMidterm Review: STAT 5301/MATH 5310 Key ConceptsDenish ShresthaNessuna valutazione finora
- Chapter 1, Part II: Predicate Logic: With Question/Answer AnimationsDocumento45 pagineChapter 1, Part II: Predicate Logic: With Question/Answer AnimationsRajiv PunjabiNessuna valutazione finora
- MATH6162 - Mathematics Week 1 LogicDocumento33 pagineMATH6162 - Mathematics Week 1 LogicDaniellaNessuna valutazione finora
- ECE523 Engineering Applications of Machine Learning and Data Analytics - Bayes and Risk - 1Documento7 pagineECE523 Engineering Applications of Machine Learning and Data Analytics - Bayes and Risk - 1wandalexNessuna valutazione finora
- Unit-3 B Predicate LogicDocumento30 pagineUnit-3 B Predicate LogicMadhav ChaudharyNessuna valutazione finora
- Towards A Unified Definition of Maximum Likelihood: Key AndphrasesDocumento11 pagineTowards A Unified Definition of Maximum Likelihood: Key AndphrasesSonya CampbellNessuna valutazione finora
- Lec 21Documento19 pagineLec 21Soumyadeep BoseNessuna valutazione finora
- FIFO and LIFO inventory costing methodsDocumento10 pagineFIFO and LIFO inventory costing methodsAnup MohapatraNessuna valutazione finora
- Different Items Can Be Controlled Independently.: 3 Single-Echelon Systems With Independent ItemsDocumento144 pagineDifferent Items Can Be Controlled Independently.: 3 Single-Echelon Systems With Independent ItemsAnup MohapatraNessuna valutazione finora
- A Study On Low-Cost Leadership Strategy PDFDocumento66 pagineA Study On Low-Cost Leadership Strategy PDFAnup MohapatraNessuna valutazione finora
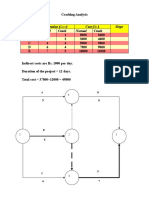
- Activity Duration (Days) Cost (RS.) Slope Normal Crash Normal CrashDocumento5 pagineActivity Duration (Days) Cost (RS.) Slope Normal Crash Normal CrashAnup MohapatraNessuna valutazione finora
- MITx SCX KeyConcept SC0x FV PDFDocumento61 pagineMITx SCX KeyConcept SC0x FV PDFJoao CarvalhoNessuna valutazione finora
- Different Items Can Be Controlled Independently.: 3 Single-Echelon Systems With Independent ItemsDocumento144 pagineDifferent Items Can Be Controlled Independently.: 3 Single-Echelon Systems With Independent ItemsAnup MohapatraNessuna valutazione finora
- JMEITOCT0305005Documento19 pagineJMEITOCT0305005Anup MohapatraNessuna valutazione finora
- Chap 8 NLPDocumento64 pagineChap 8 NLPAnup MohapatraNessuna valutazione finora
- Problem Statement: 1) Capacity of Beds 2) Maintaining Quality Standards 3) Scheduling of Tasks 4) Resource UtilizationDocumento1 paginaProblem Statement: 1) Capacity of Beds 2) Maintaining Quality Standards 3) Scheduling of Tasks 4) Resource UtilizationAnup MohapatraNessuna valutazione finora
- Shifting of Loyalties: Perception of Telecom Customers After Launching of "Jio" in Jalgaon CityDocumento7 pagineShifting of Loyalties: Perception of Telecom Customers After Launching of "Jio" in Jalgaon CityAnup MohapatraNessuna valutazione finora
- Case Study: Apple Inc. in 2015Documento19 pagineCase Study: Apple Inc. in 2015Anup MohapatraNessuna valutazione finora
- Asset ManagementDocumento2 pagineAsset ManagementAnup MohapatraNessuna valutazione finora
- 2015 2016 Heinz College, School of ISM COA 12.04.2014Documento2 pagine2015 2016 Heinz College, School of ISM COA 12.04.2014bluegreenblackNessuna valutazione finora
- Asset Management Intern Recommendation WriteupDocumento2 pagineAsset Management Intern Recommendation WriteupAnup MohapatraNessuna valutazione finora
- Pricing: Presentation by Group 5Documento49 paginePricing: Presentation by Group 5Anup MohapatraNessuna valutazione finora
- Hospital Case CardiacDocumento3 pagineHospital Case CardiacAnup MohapatraNessuna valutazione finora
- SouthWest Airlines Case StudyDocumento9 pagineSouthWest Airlines Case StudySalman ShahzadNessuna valutazione finora
- QM 1 Solution PG: 427 Q: 60Documento1 paginaQM 1 Solution PG: 427 Q: 60Anup MohapatraNessuna valutazione finora
- New Company ProfileDocumento21 pagineNew Company ProfileAnup Mohapatra50% (2)
- The Enron ScandalDocumento14 pagineThe Enron ScandalAnup MohapatraNessuna valutazione finora
- Enron Business & Financial ModelDocumento7 pagineEnron Business & Financial ModelAnup MohapatraNessuna valutazione finora
- Quick Formulas Financial AnalysisDocumento9 pagineQuick Formulas Financial AnalysisAnup MohapatraNessuna valutazione finora
- Texas A&M MSADO Assignment 4 Optimization AlgorithmsDocumento3 pagineTexas A&M MSADO Assignment 4 Optimization AlgorithmsBobaNessuna valutazione finora
- 2019-20 University PaperDocumento2 pagine2019-20 University PaperKhushi PachauriNessuna valutazione finora
- Algorithm Design and Analysis NotesDocumento42 pagineAlgorithm Design and Analysis NotesMD NADEEM ASGARNessuna valutazione finora
- Leonen, Christian Rouel C - Bisection Method - EEP312Documento4 pagineLeonen, Christian Rouel C - Bisection Method - EEP312Rouel LeonenNessuna valutazione finora
- TOSDocumento1 paginaTOSChona dela cruzNessuna valutazione finora
- Design and Analysis of AlgorithmsDocumento1 paginaDesign and Analysis of AlgorithmsprinceNessuna valutazione finora
- Worksheet Method of Lagrange MultipliersDocumento2 pagineWorksheet Method of Lagrange MultipliersVanessa HardjadinataNessuna valutazione finora
- Numerical Analysis - Truncation and Taylor SeriesDocumento25 pagineNumerical Analysis - Truncation and Taylor SeriesTommy FuNessuna valutazione finora
- Factorización de PolinomiosDocumento27 pagineFactorización de PolinomiosEdwin LlantoyNessuna valutazione finora
- DAA Module 3 Power Point-S.MercyDocumento56 pagineDAA Module 3 Power Point-S.MercyIshita SinghalNessuna valutazione finora
- Sham Daa MCQDocumento2 pagineSham Daa MCQshambhand202067% (3)
- No - Meth Jrock Vol2 PDFDocumento667 pagineNo - Meth Jrock Vol2 PDFSanjoy PathakNessuna valutazione finora
- Lecture 5 - Solving Systems of Linear Equations (Gauss-Jordan Elimination Method)Documento8 pagineLecture 5 - Solving Systems of Linear Equations (Gauss-Jordan Elimination Method)Mark Joseph PanongNessuna valutazione finora
- Polynomial Q PDFDocumento44 paginePolynomial Q PDFnareshganeshNessuna valutazione finora
- Experiment 2a2q2020Documento25 pagineExperiment 2a2q2020Frenchesca Darlene CaliwliwNessuna valutazione finora
- Newey-West EstimatorDocumento3 pagineNewey-West Estimatordev414Nessuna valutazione finora
- Simple Neural Nets For Pattern ClassificationDocumento68 pagineSimple Neural Nets For Pattern ClassificationsukruthNessuna valutazione finora
- Computer Oriented Numerical Methods 4Documento2 pagineComputer Oriented Numerical Methods 4Theophilus ParateNessuna valutazione finora
- CSN-212 Algorithms Sorting Techniques TutorialDocumento3 pagineCSN-212 Algorithms Sorting Techniques TutorialROHIT RAJNessuna valutazione finora
- Numerical Integration: Joko Wintoko Matematika Teknik Kimia 2 JTK/FT/UGM/2011Documento44 pagineNumerical Integration: Joko Wintoko Matematika Teknik Kimia 2 JTK/FT/UGM/2011Agnes PascaliaNessuna valutazione finora
- SOAL 'N' JAWABAN SPK P. RUZARDIDocumento17 pagineSOAL 'N' JAWABAN SPK P. RUZARDIFajar RachmantoNessuna valutazione finora
- BCSL 045 Solved Assignment 2021Documento13 pagineBCSL 045 Solved Assignment 2021vishwasNessuna valutazione finora
- 3 InterpolationDocumento32 pagine3 InterpolationImrul HasanNessuna valutazione finora
- MCQDocumento2 pagineMCQraj8kanungoNessuna valutazione finora
- Title: Overview:: Ai Lab Mini ProjectDocumento5 pagineTitle: Overview:: Ai Lab Mini ProjectMAYURI PAWARNessuna valutazione finora
- Hierarchical ClusteringDocumento8 pagineHierarchical ClusteringRavindra Kumar PrajapatiNessuna valutazione finora