Documenti di Didattica
Documenti di Professioni
Documenti di Cultura
Chapter 3: Quadratic Functions 3.1 Quadratic Functions and Their Graphs General Form of Quadratic Function
Caricato da
Shafiqah SamsuriDescrizione originale:
Titolo originale
Copyright
Formati disponibili
Condividi questo documento
Condividi o incorpora il documento
Hai trovato utile questo documento?
Questo contenuto è inappropriato?
Segnala questo documentoCopyright:
Formati disponibili
Chapter 3: Quadratic Functions 3.1 Quadratic Functions and Their Graphs General Form of Quadratic Function
Caricato da
Shafiqah SamsuriCopyright:
Formati disponibili
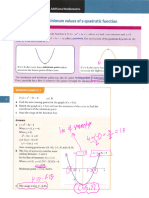
CHAPTER 3: QUADRATIC FUNCTIONS
3.1 Quadratic Functions and Their Graphs
General form of quadratic function
General form of a quadratic function is
f(x) = ax2 + bx + c
Example 1
Determine which of the following is a quadratic function.
1. f(x) = (5x 3)(3x + 8)
2. f(x) = 2(3x + 8)
5
f ( x )= 2
3.
2x
The graph of quadratic function
The graph of quadratic function is parabola.
When the coefficient of x2 is positive, the graph is a parabola with shape.
When the coefficient of x2 is negative, the graph is a parabola with shape.
Axis of symmetry
A vertical line passing through the maximum or minimum point of parabola.
a>0
a<0
Page 1 of 4
Relation between the position of the graph of a quadratic function f(x) and the
type of roots for f(x) = 0
b2 4ac > 0
b2 4ac = 0
b2 4ac < 0
Example 2
Given that the graph of a quadratic function f(x) = x2 + 2x + 1 k intersects the x-axis
at two different points, find the range of values of k.
Page 2 of 4
3.2 Maximum and Minimum Values of Quadratic Functions
Maximum and minimum point
A quadratic functions f(x) = ax2 + bx + c can be expressed in the form
f(x) = a(x + p)2 + q by the method of completing the square.
The minimum or maximum point can be determined from the equation in the form
of f(x) = a(x + p)2 + q.
Minimum Point
The quadratic function f(x) has a
minimum value if a is positive.
The quadratic function f(x) has a
minimum value when (x + p) = 0.
The minimum value is equal to q.
Thus, the minimum point is (-p, q).
Maximum Point
The quadratic function f(x) has a
maximum value if a is negative.
The quadratic function f(x) has a
maximum value when (x + p) = 0.
The maximum value is equal to q.
Thus, the maximum point is (-p, q).
Example 3
Find the maximum or minimum point of the following quadratic equations.
1. f(x) = (x 3)2 + 7
2. f(x) = -5 3(x + 15)2
Finding the maximum and minimum points of quadratic function using
completing the square
Step 2:
Make sure the coefficient x2 is 1, if not, factorize.
coefficient of x 2 coefficient of x 2
+(
) (
) .
Insert
2
2
Step 3:
Completing the square.
Step 1:
Example 4
Find the maximum or minimum value each of the following quadratic function by
completing the squares. In each case, state the value of x at which the function is
maximum or minimum. And also, state the maximum or minimum point and axis of
symmetry for each case.
1.
2.
3.
4.
f(x) = x2 + 6x + 7
f(x) = 2x2 6x + 7
f(x) = 5 2x x2
f(x) = 4 + 12x 3x2
Page 3 of 4
3.3 Sketching the Graphs of Quadratic Functions
To sketch the graph of a quadratic function, you need to show
1. the shape of the graph
2. the maximum or minimum point of the graph
3. the x-intercept of the graph
4. the y-intercept of the graph
Example 5
Sketch the curve of the quadratic function f(x) = x2 x 12.
3.4 Quadratic Inequalities
Steps to solve a quadratic inequality
Step 1: Rewrite the inequality with zero on one side and make sure a > 0.
Step 2: Find where it crosses the x-axis (y = 0).
Step 3: Sketch the graph and shade the region to find the range of values of x.
Example 6
Find the range of values of x for each of the following.
1. x2 4x + 3 < 0
2. 12 + 10x 2x2 < 0
Page 4 of 4
Potrebbero piacerti anche
- A-level Maths Revision: Cheeky Revision ShortcutsDa EverandA-level Maths Revision: Cheeky Revision ShortcutsValutazione: 3.5 su 5 stelle3.5/5 (8)
- Lesson 3 Quad Functions and Polynomisl Functions of Higher DegreeDocumento59 pagineLesson 3 Quad Functions and Polynomisl Functions of Higher DegreeMa. Consuelo Melanie Cortes IIINessuna valutazione finora
- Quadratic Function and Factoring Quadractic EquationDocumento14 pagineQuadratic Function and Factoring Quadractic EquationYvan OmayanNessuna valutazione finora
- Section 2.3 Polynomial Functions and Their GraphsDocumento31 pagineSection 2.3 Polynomial Functions and Their GraphsdavogezuNessuna valutazione finora
- Chapter 3 - Quadratc Functions (Pearl™)Documento11 pagineChapter 3 - Quadratc Functions (Pearl™)Umair HishamNessuna valutazione finora
- Maths in Focus - Margaret Grove - ch9Documento34 pagineMaths in Focus - Margaret Grove - ch9Sam Scheding0% (1)
- LONG Dokumen Pub Cambridge Igcse and o Level Additional MathematicsDocumento5 pagineLONG Dokumen Pub Cambridge Igcse and o Level Additional MathematicsOmar HamwiNessuna valutazione finora
- Functions (Part 2)Documento10 pagineFunctions (Part 2)Ankur GoelNessuna valutazione finora
- PC Exam ReviewDocumento4 paginePC Exam Reviewklb925Nessuna valutazione finora
- ch10 PDFDocumento36 paginech10 PDFcathyNessuna valutazione finora
- Quad FN Worksheet 4Documento7 pagineQuad FN Worksheet 4jan12th2004Nessuna valutazione finora
- Rational Functions: Rational Functions Are Quotients of Polynomial Functions. This Means ThatDocumento16 pagineRational Functions: Rational Functions Are Quotients of Polynomial Functions. This Means ThatSalih AnwarNessuna valutazione finora
- Unit 9 Lesson NotesDocumento22 pagineUnit 9 Lesson Notesapi-291793268Nessuna valutazione finora
- 3.0 Review FunctionsDocumento12 pagine3.0 Review Functionsummu***Nessuna valutazione finora
- Genmath Module 6Documento9 pagineGenmath Module 6Jenray DacerNessuna valutazione finora
- Coordinate Geometry IIDocumento41 pagineCoordinate Geometry IIkrish1092pNessuna valutazione finora
- Ch10 The Quadratic FunctionDocumento36 pagineCh10 The Quadratic Functiontrantuanan123Nessuna valutazione finora
- Quadratic Functions: A A Shape ParameterDocumento8 pagineQuadratic Functions: A A Shape ParameterMuhammad Syarif100% (1)
- Lecture 3Documento3 pagineLecture 3Hari KrishnaNessuna valutazione finora
- 3 2 LessonDocumento31 pagine3 2 Lessonapi-261587850Nessuna valutazione finora
- Find x and y intercepts of polynomial functionsDocumento21 pagineFind x and y intercepts of polynomial functionsjudeNessuna valutazione finora
- Math 10.4Documento15 pagineMath 10.4bea sailNessuna valutazione finora
- Linear Functions Linear FunctionsDocumento8 pagineLinear Functions Linear FunctionsNerinel CoronadoNessuna valutazione finora
- Chapter 3-Quadratic Functions: C BX Ax X FDocumento11 pagineChapter 3-Quadratic Functions: C BX Ax X FSiti Fairus MohammadNessuna valutazione finora
- Polynomial Function: PX Ax Ax Ax AxaDocumento15 paginePolynomial Function: PX Ax Ax Ax AxautpNessuna valutazione finora
- Quadratic Functions UnitDocumento7 pagineQuadratic Functions UnitmicjenNessuna valutazione finora
- Determinet The Domain of Rational Functions Identify Vertical or Horizontal Asymptotes Graphs Rational FunctionsDocumento13 pagineDeterminet The Domain of Rational Functions Identify Vertical or Horizontal Asymptotes Graphs Rational Functionsm29402102Nessuna valutazione finora
- Add Maths Study NotesDocumento61 pagineAdd Maths Study NotesElisha James100% (1)
- Topics Entry Test IBEB NonCD Version 2014Documento5 pagineTopics Entry Test IBEB NonCD Version 2014YonYonNessuna valutazione finora
- Vertical and Horizontal Asymptotes of Rational FunctionsDocumento2 pagineVertical and Horizontal Asymptotes of Rational Functionsscarlet100% (2)
- Quadratic Functions: A Visual Guide to ParabolasDocumento25 pagineQuadratic Functions: A Visual Guide to ParabolasCherry Grace Sagde EuldanNessuna valutazione finora
- Functions and Continuity Functions and Continuity Functions and Continuity Functions and ContinuityDocumento22 pagineFunctions and Continuity Functions and Continuity Functions and Continuity Functions and ContinuityUmesh ChaturvediNessuna valutazione finora
- Polynomial Functions and Their GraphsDocumento14 paginePolynomial Functions and Their GraphsDr Milan Glendza Petrovic Njegos0% (1)
- Math Worksheet-Graphing of FunctionsDocumento7 pagineMath Worksheet-Graphing of FunctionsEducareLabNessuna valutazione finora
- PolynomialsDocumento42 paginePolynomialsapi-296824694Nessuna valutazione finora
- Lesson 6 Grade 10 MathematicsDocumento2 pagineLesson 6 Grade 10 MathematicsMarieanne SantosNessuna valutazione finora
- Graphs of Polynomial Functions: Grade 10 MathematicsDocumento2 pagineGraphs of Polynomial Functions: Grade 10 MathematicsMarieanne SantosNessuna valutazione finora
- Topic 1: QuadraticsDocumento13 pagineTopic 1: QuadraticsKaness Mathz100% (1)
- Basic Calculus: Derivatives ExplainedDocumento25 pagineBasic Calculus: Derivatives ExplainedKrrje INessuna valutazione finora
- Quadratic Functions: A A Shape ParameterDocumento8 pagineQuadratic Functions: A A Shape ParameterAna Dela FuenteNessuna valutazione finora
- A Quadratic FunctionDocumento8 pagineA Quadratic FunctionMaikka IlaganNessuna valutazione finora
- Quadratic FunctionsDocumento20 pagineQuadratic FunctionsSalmizam IzamNessuna valutazione finora
- 3 Quadratic FunctionDocumento12 pagine3 Quadratic FunctionTANG PEI PEI100% (10)
- Polynomial Functions Unit Assignment PDFDocumento10 paginePolynomial Functions Unit Assignment PDFShaiel Fabiana Redondo QuinteroNessuna valutazione finora
- Quadraric Functions Soalan SPMDocumento5 pagineQuadraric Functions Soalan SPMBariza BaharomNessuna valutazione finora
- Graphing Polynomial FunctionsDocumento19 pagineGraphing Polynomial Functionshcnè dynnNessuna valutazione finora
- 2.6.3 Practice - Quadratic Functions (Practice)Documento11 pagine2.6.3 Practice - Quadratic Functions (Practice)johnnyhockey91Nessuna valutazione finora
- Polynomial and Rational FunctionsDocumento66 paginePolynomial and Rational FunctionsArc Daniel C. CabreraNessuna valutazione finora
- Euclid Stage 3 Class 2 Notes Algebra 2 (Polynomials and FloorDocumento7 pagineEuclid Stage 3 Class 2 Notes Algebra 2 (Polynomials and FloorHappy Dolphin100% (1)
- 2 Evaluating FunctionsDocumento20 pagine2 Evaluating Functions8fzggdnv5wNessuna valutazione finora
- Polynomial functions and factoring techniquesDocumento43 paginePolynomial functions and factoring techniquesAnonymous na314kKjOANessuna valutazione finora
- MATHALGIIBU12Quadratic_FunctionsDocumento22 pagineMATHALGIIBU12Quadratic_FunctionsMbocaBentoNessuna valutazione finora
- Quadratic Functions-Hoboken2Documento76 pagineQuadratic Functions-Hoboken2Melani NaneaNessuna valutazione finora
- Mat 104 Tutorials Set 1 PDFDocumento2 pagineMat 104 Tutorials Set 1 PDFKwadwo Appiah-BoatengNessuna valutazione finora
- Advanced Algeb ProjectDocumento17 pagineAdvanced Algeb ProjectdiomNessuna valutazione finora
- Lesson 3 Quadratic FunctionsDocumento13 pagineLesson 3 Quadratic FunctionsChet Jerry AckNessuna valutazione finora
- The Graph of A Quadratic FunctionDocumento30 pagineThe Graph of A Quadratic FunctionIr HeriawanNessuna valutazione finora
- Lesson 15 - Graph of A Quadratic Function...Documento10 pagineLesson 15 - Graph of A Quadratic Function...jiemma parillaNessuna valutazione finora
- Evaluate Functions Using SubstitutionDocumento41 pagineEvaluate Functions Using SubstitutionNikoru KatakanaNessuna valutazione finora
- Chapter 2Documento22 pagineChapter 2Shafiqah SamsuriNessuna valutazione finora
- Chapter 3Documento7 pagineChapter 3Shafiqah SamsuriNessuna valutazione finora
- Chapter 10: Solution of Triangles 10.1 Sine RuleDocumento4 pagineChapter 10: Solution of Triangles 10.1 Sine RuleShafiqah SamsuriNessuna valutazione finora
- Chapter 8: Circular Measure 8.1 Radian: Length of ArcDocumento3 pagineChapter 8: Circular Measure 8.1 Radian: Length of ArcShafiqah SamsuriNessuna valutazione finora
- Exercise Chapter 11Documento3 pagineExercise Chapter 11Shafiqah SamsuriNessuna valutazione finora
- Exercise Chapter 7Documento2 pagineExercise Chapter 7Shafiqah SamsuriNessuna valutazione finora
- Chapter 11: Index Number 11.1 Index Number Price Index: Page 1 of 3Documento3 pagineChapter 11: Index Number 11.1 Index Number Price Index: Page 1 of 3Shafiqah SamsuriNessuna valutazione finora
- Exercise Chapter 11Documento3 pagineExercise Chapter 11Shafiqah SamsuriNessuna valutazione finora
- Exercise Chapter 10Documento2 pagineExercise Chapter 10Shafiqah SamsuriNessuna valutazione finora
- When y A, Then Dy DX When y X, Then Dy DX NX When y Ax, Then Dy DX A When y A X, Then Dy DX Anx When y X, Then Dy DX N X When y A X, Then Dy DX A XDocumento1 paginaWhen y A, Then Dy DX When y X, Then Dy DX NX When y Ax, Then Dy DX A When y A X, Then Dy DX Anx When y X, Then Dy DX N X When y A X, Then Dy DX A XShafiqah SamsuriNessuna valutazione finora
- Chapter 7: Statistics 7.1 Measures of Central Tendency 7.1.1 MeanDocumento13 pagineChapter 7: Statistics 7.1 Measures of Central Tendency 7.1.1 MeanShafiqah Samsuri100% (1)
- Exercise Chapter 8Documento5 pagineExercise Chapter 8Shafiqah SamsuriNessuna valutazione finora
- Chapter 6: Coordinate Geometry 6.1 Distance Between Two PointsDocumento11 pagineChapter 6: Coordinate Geometry 6.1 Distance Between Two PointsShafiqah SamsuriNessuna valutazione finora
- Exercise Chapter 6Documento4 pagineExercise Chapter 6Shafiqah SamsuriNessuna valutazione finora
- Exercise Chapter 4Documento1 paginaExercise Chapter 4Shafiqah SamsuriNessuna valutazione finora
- When A Real Number A Is Multiplied by Itself in N Times, The Result Is The A To The Power of N. in GeneralDocumento9 pagineWhen A Real Number A Is Multiplied by Itself in N Times, The Result Is The A To The Power of N. in GeneralShafiqah SamsuriNessuna valutazione finora
- Solve Simultaneous Equations & Geometry ProblemsDocumento2 pagineSolve Simultaneous Equations & Geometry ProblemsShafiqah SamsuriNessuna valutazione finora
- Exercise Chapter 5Documento1 paginaExercise Chapter 5Shafiqah SamsuriNessuna valutazione finora
- Chapter 3 ExerciseDocumento1 paginaChapter 3 ExerciseShafiqah SamsuriNessuna valutazione finora
- Kertas 1 Pep BK1 SPM Terengganu 2016 - SoalanDocumento35 pagineKertas 1 Pep BK1 SPM Terengganu 2016 - SoalanShafiqah SamsuriNessuna valutazione finora
- Functions ChapterDocumento7 pagineFunctions ChapterShafiqah SamsuriNessuna valutazione finora
- Chapter 2Documento6 pagineChapter 2Shafiqah SamsuriNessuna valutazione finora
- OSHA Process Safety ManagementDocumento18 pagineOSHA Process Safety ManagementShafiqah Samsuri100% (1)
- Exercise Chapter 1Documento4 pagineExercise Chapter 1Shafiqah SamsuriNessuna valutazione finora
- Choocoby Snack Company ReportDocumento54 pagineChoocoby Snack Company ReportShafiqah Samsuri100% (1)
- Fundamentals of Fires and ExplosionsDocumento4 pagineFundamentals of Fires and ExplosionsShafiqah SamsuriNessuna valutazione finora
- Schlumberger Log Interpretation ChatsDocumento287 pagineSchlumberger Log Interpretation ChatsSabrianto AswadNessuna valutazione finora
- Cracking Moment Analysis of Prestressed Concrete BeamDocumento18 pagineCracking Moment Analysis of Prestressed Concrete Beamharshil gandhiNessuna valutazione finora
- Equilibrium Stage Processes - Docx CetDocumento25 pagineEquilibrium Stage Processes - Docx CetPortia ShilengeNessuna valutazione finora
- Design of Gain Compensator: DR Mirza Tariq HamayunDocumento19 pagineDesign of Gain Compensator: DR Mirza Tariq HamayunAsad RehanNessuna valutazione finora
- Standing Waves On A StringDocumento6 pagineStanding Waves On A StringamirpouyanNessuna valutazione finora
- CE272 Fluid MechanicsDocumento56 pagineCE272 Fluid MechanicsHasan KırmızıoğlanNessuna valutazione finora
- Cem - Part 1 PDFDocumento19 pagineCem - Part 1 PDFDavin OtogleNessuna valutazione finora
- Separation and Purification of Triacylglycerols From Nyamplung (Calophyllum Inophyllum) Oil by Batchwise Solvent ExtractionDocumento24 pagineSeparation and Purification of Triacylglycerols From Nyamplung (Calophyllum Inophyllum) Oil by Batchwise Solvent ExtractionAfifatul JannahNessuna valutazione finora
- Reka Bentuk, Pembinaan Dan Pentadbiran UjianDocumento9 pagineReka Bentuk, Pembinaan Dan Pentadbiran UjianAiman HazimNessuna valutazione finora
- Ising ModelDocumento5 pagineIsing Modeldecerto252Nessuna valutazione finora
- Alarms Manual (ENGLISH)Documento12 pagineAlarms Manual (ENGLISH)FadFadNessuna valutazione finora
- How retinal adaptation maintains visual perception despite illumination changesDocumento1 paginaHow retinal adaptation maintains visual perception despite illumination changesAkicaNessuna valutazione finora
- Forensic Chemistry ToxicologyDocumento139 pagineForensic Chemistry ToxicologyCeasar Estrada94% (18)
- Pore Structure of Air-Entrained Hardened Cement PasteDocumento9 paginePore Structure of Air-Entrained Hardened Cement Paste1mattelliottNessuna valutazione finora
- P Ractical Approaches To Fast Gas Chromatography-Mass Spectrometry Muy BuenoDocumento28 pagineP Ractical Approaches To Fast Gas Chromatography-Mass Spectrometry Muy BuenoJavier Joao Lloyd IglesiasNessuna valutazione finora
- TMTL2400KDocumento4 pagineTMTL2400KRushit ShahNessuna valutazione finora
- Diaphragm Design PDFDocumento50 pagineDiaphragm Design PDFManoj JaiswalNessuna valutazione finora
- Analysis of Wood Bending PropertiesDocumento11 pagineAnalysis of Wood Bending Propertiesprasanna020391100% (1)
- Chapter 1 Lecture1Documento39 pagineChapter 1 Lecture1Anonymous AFFiZnNessuna valutazione finora
- OAT Bootcamp Physics Equation Sheet PDFDocumento11 pagineOAT Bootcamp Physics Equation Sheet PDFjon100% (2)
- Chemistry Test 1 July 2019 BatchDocumento3 pagineChemistry Test 1 July 2019 BatchDaNessuna valutazione finora
- 8.012 Physics I: Classical Mechanics: Mit OpencoursewareDocumento8 pagine8.012 Physics I: Classical Mechanics: Mit OpencoursewareAlexandru CiobanuNessuna valutazione finora
- Molecular Partition Function ExplainedDocumento18 pagineMolecular Partition Function ExplainedAnimasahun Olamide HammedNessuna valutazione finora
- Differential Equations and Linear Algebra Lectura NotesDocumento96 pagineDifferential Equations and Linear Algebra Lectura NotesClaudioTRodriguesNessuna valutazione finora
- E401Documento4 pagineE401Katrina BucudNessuna valutazione finora
- Conduction, Convection, & RadiationDocumento14 pagineConduction, Convection, & Radiationyuvionfire100% (1)
- Lahore University of Management Sciences: EE539 - Radar SystemsDocumento3 pagineLahore University of Management Sciences: EE539 - Radar SystemsDr-Raghad Al-FahamNessuna valutazione finora
- Math at Grade 4Documento9 pagineMath at Grade 4api-239942675Nessuna valutazione finora
- Ezy Math Tutoring - Year 9 AnswersDocumento144 pagineEzy Math Tutoring - Year 9 AnswersVincents Genesius EvansNessuna valutazione finora
- Cylinders Shall Be Produced As Per IS 7285 and Approved by Chief Controller of ExplosiveDocumento1 paginaCylinders Shall Be Produced As Per IS 7285 and Approved by Chief Controller of ExplosiveAlanka Prasad100% (1)