10/20/2015

Y- transform - Wikipedia, the free encyclopedia

Y- transform
From Wikipedia, the free encyclopedia

This article is about the mathematical technique. For the device which transforms three-phase electric
power without a neutral wire into three-phase power with a neutral wire, see delta-wye transformer.
For the application in statistical mechanics see, see YangBaxter equation. For the regional airline
brand name for Delta Air Lines, see Delta Connection.
The Y- transform, also written wye-delta and also known by many other names, is a mathematical
technique to simplify the analysis of an electrical network. The name derives from the shapes of the circuit
diagrams, which look respectively like the letter Y and the Greek capital letter . This circuit
transformation theory was published by Arthur Edwin Kennelly in 1899.[1] It is widely used in analysis of
three-phase electric power circuits.
The Y- transform can be considered a special case of the star-mesh transform for three resistors. In
mathematics, the Y- transform plays an important role in theory of circular planar graphs.[2]

Contents
1 Names
2 Basic Y- transformation
2.1 Equations for the transformation from to Y
2.2 Equations for the transformation from Y to
2.3 Circuit Analysis: Techniques for Solving to Y
3 A proof of the existence and uniqueness of the transformation
4 Simplification of networks
5 Graph theory
6 Demonstration
6.1 -load to Y-load transformation equations
6.2 Y-load to -load transformation equations
7 See also
8 Notes
9 References
10 External links

Names
The Y- transform is known by a variety of other
names, mostly based upon the two shapes involved,
listed in either order. The Y, spelled out as wye, can
also be called T or star; the , spelled out as delta,
can also be called triangle, (spelled out as pi), or
mesh. Thus, common names for the transformation
include wye-delta or delta-wye, star-delta, starmesh, or T-.

Illustration of the transform in its T-

representation.

Basic Y- transformation
https://en.wikipedia.org/wiki/Y-%CE%94_transform

1/8

10/20/2015

Y- transform - Wikipedia, the free encyclopedia

The transformation is used to establish equivalence for

networks with three terminals. Where three elements
terminate at a common node and none are sources, the
node is eliminated by transforming the impedances.
For equivalence, the impedance between any pair of
terminals must be the same for both networks. The
equations given here are valid for complex as well as
real impedances.

Equations for the transformation from to

Y
The general idea is to compute the impedance
to adjacent node in the circuit by

where

and Y circuits with the labels which are used in

this article.

at a terminal node of the Y circuit with impedances

are all impedances in the circuit. This yields the specific formulae

Equations for the transformation from Y to

The general idea is to compute an impedance

in the circuit by

where
is the sum of the products of all pairs of impedances in the Y
circuit and
is the impedance of the node in the Y circuit which is opposite the edge with
.
The formula for the individual edges are thus

Circuit Analysis: Techniques for Solving to Y

https://en.wikipedia.org/wiki/Y-%CE%94_transform

2/8

10/20/2015

Y- transform - Wikipedia, the free encyclopedia

A circuit that has a combination of -loads and Y-loads should be converted to the Y configuration. By
converting from to Y, each circuit element can be analyzed separately. Converting from to Y is a
technique aimed to simplify circuit analysis. (Note: harmonic behavior from the original circuit remained
unchanged). The conversion from the notation to Y notation is as follows.

A proof of the existence and uniqueness of the transformation

The feasibility of the transformation can be shown as a consequence of superposition theorem in electric
circuit. A short proof, rather than derived as a corollary of the more general star-mesh transform, can be
given as follows. The equivalence lies in the statement that for any external voltages ( ,
and )
applying at the three nodes ( ,
and
), the corresponding currents ( ,
and ) are exactly the
same for both the Y and circuit, and vice versa. In this proof, we start with given external currents at the
nodes. According to superposition theorem, the voltages can be obtained by studying the linear summation
of the resulting voltages at the nodes of following three problems: apply at the three nodes with current (1)
,
, , (2) ,
,
and (3)
, ,
. It can be readily shown that due to Kirchhoff's circuit laws, one has
.
One notes that now each problem is relatively simple, since it only involves one single ideal current
source. To obtain exactly the same outcome voltages at the nodes for each problem, the equivalent
resistances in two circuits must be the same, this can be easily found by using the basic rules of series and
parallel circuits:

Though usually six equations are more than enough to express three variables (
) in term of
the other three variables(
), here it is straightforward to show that these equations indeed lead
to the above designed expressions. In fact, the superposition theorem not only establishes the relation
between the values of the resistances, but also guarantees the uniqueness of such solution.

Simplification of networks
Resistive networks between two terminals can theoretically be simplified to a single equivalent resistor
(more generally, the same is true of impedance). Series and parallel transforms are basic tools for doing
so, but for complex networks such as the bridge illustrated here, they do not suffice.
The Y- transform can be used to eliminate one node at a time and produce a network that can be further
simplified, as shown.

https://en.wikipedia.org/wiki/Y-%CE%94_transform

3/8

10/20/2015

Y- transform - Wikipedia, the free encyclopedia

Transformation of a bridge resistor network, using the Y- transform to eliminate

node D, yields an equivalent network that may readily be simplified further.

The reverse transformation, -Y, which adds a node, is often handy to pave the way for further
simplification as well.

Transformation of a bridge resistor network, using the Y transform, also yields an equivalent network that may
readily be simplified further.

Every two-terminal network represented by a planar graph can be reduced to a single equivalent resistor
by a sequence of series, parallel, Y-, and -Y transformations.[3] However, there are non-planar
networks that cannot be simplified using these transformations, such as a regular square grid wrapped
around a torus, or any member of the Petersen family.

Graph theory
In graph theory, the Y- transform means replacing a Y subgraph of a graph with the equivalent
subgraph. The transform preserves the number of edges in a graph, but not the number of vertices or the
number of cycles. Two graphs are said to be Y- equivalent if one can be obtained from the other by a
series of Y- transforms in either direction. For example, the Petersen family is a Y- equivalence class.

Demonstration
-load to Y-load transformation equations
To relate
from to
from Y, the impedance between two corresponding
nodes is compared. The impedance in either configuration is determined as if one of the nodes is
disconnected from the circuit.
https://en.wikipedia.org/wiki/Y-%CE%94_transform

4/8

10/20/2015

Y- transform - Wikipedia, the free encyclopedia

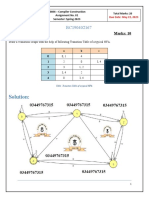
The impedance between N1 and N2 with N3 disconnected in :

To simplify, let
.

be the sum of
and Y circuits with the labels that are used in this
article.

Thus,

The corresponding impedance between N1 and N2 in Y is simple:

hence:
(1)
Repeating for

:
(2)

and for

:
(3)

From here, the values of

subtraction).

can be determined by linear combination (addition and/or

For example, adding (1) and (3), then subtracting (2) yields

thus,
https://en.wikipedia.org/wiki/Y-%CE%94_transform

5/8

10/20/2015

Y- transform - Wikipedia, the free encyclopedia

where
For completeness:
(4)

(5)

(6)

Y-load to -load transformation equations

Let
.
We can write the to Y equations as
(1)

(2)

(3)
Multiplying the pairs of equations yields
(4)

(5)

https://en.wikipedia.org/wiki/Y-%CE%94_transform

6/8

10/20/2015

Y- transform - Wikipedia, the free encyclopedia

(6)
and the sum of these equations is
(7)
Factor
denominator.

from the right side, leaving

in the numerator, canceling with an

in the

(8)
Note the similarity between (8) and {(1),(2),(3)}
Divide (8) by (1)

which is the equation for

equations.

. Dividing (8) by (2) or (3) (expressions for

or

) gives the remaining

See also
Star-mesh transform
Analysis of resistive circuits
Electrical network, single-phase electric power, alternating-current electric power, three-phase
power, polyphase systems for examples of Y and connections
AC motor for a discussion of the Y- starting technique
Nikola Tesla
John Hopkinson
Mikhail Dolivo-Dobrovolsky
Charles Proteus Steinmetz

Notes
1. A.E. Kennelly, "Equivalence of triangles and three-pointed stars in conducting networks", Electrical World and
Engineer, vol. 34, pp. 413414, 1899.
2. E.B. Curtis, D. Ingerman, J.A. Morrow, Circular planar graphs and resistor networks
(http://www.sciencedirect.com/science/article/pii/S0024379598100873), Linear Algebra and its Applications,
vol. 238, pp. 115150, 1998.
3. Klaus Truemper. On the delta-wye reduction for planar graphs
(http://onlinelibrary.wiley.com/doi/10.1002/jgt.3190130202/abstract). J. Graph Theory 13(2):141148, 1989.
https://en.wikipedia.org/wiki/Y-%CE%94_transform

7/8

10/20/2015

Y- transform - Wikipedia, the free encyclopedia

References
William Stevenson, Elements of Power System Analysis 3rd ed., McGraw Hill, New York, 1975,
ISBN 0-07-061285-4

External links
Star-Triangle Conversion (http://www.designcabana.com/knowledge/electrical/basics/resistors):
Knowledge on resistive networks and resistors
Calculator of Star-Triangle transform (http://www.elektroenergetika.cz/calculations/transfigurace.php?language=english)
Retrieved from "https://en.wikipedia.org/w/index.php?title=Y-_transform&oldid=680052020"
Categories: Electrical circuits Electric power Graph operations Circuit theorems
This page was last modified on 8 September 2015, at 11:56.
Text is available under the Creative Commons Attribution-ShareAlike License; additional terms
may apply. By using this site, you agree to the Terms of Use and Privacy Policy. Wikipedia is a
registered trademark of the Wikimedia Foundation, Inc., a non-profit organization.

https://en.wikipedia.org/wiki/Y-%CE%94_transform

8/8