249

2. Nond;meru;onal Paramt!tt!rs Dnerm;ned from Difft!rential Equations

Chapter8

understanding of dynamic similarity is also important in theoretical fluid

mechanics, especially when simplifications are to be made. Under various
limiting situations certain variables can be eliminated from our consideration,
resulting in very useful relationships in which 'only the constants need to be
determined from experiments. Such a procedure is used extensively in turbulence theory, and leads for example to the well-known K- S /3 spectral law
discussed in Chapter 12; analogous arguments (applied to a difIerent problem)
are presented in Section 5 of the present chapter.
Nondimensional parameters for a problem can be determined in two ways.
They can be deduced directly from the governing diflerential equations if these
equations are known; this method is illustrated in the next section. If, on the
other hand, the governing difIerential equations are unknown, th~he' nondimensional parameters can be determined by performing a simple dimensional
analysis on the variables involved. This method is iIlustrated in Section 4.

Dynamic Similarity
1. 1ntroduction ..................
2. Nondimensional Parameters
Determined Irom Differential
Equations ....................
3. Dimensional Matrix ...........
4. Buckingham's Pi Teorem ......
5. Nondimensional Parameters and
Dynamic Similarity ............

248
249
252
253
255

Prediction of Flow Behavior from

Dimensional Considerations ..... 257

2. Nondimensional Parameters Determined from

Differential Equations

7. Significance 01 Common
Nondimensional Parameters

259
260
260
260
261
261
261
Exercises ..................... 262

Reynolds Number ..............

Froude Number ................
Internal Froude N'umber .........
Richardson Number ........... oo.oo.
Mach Number .................
Prandtl Number ...............

To illustrate the method of determining nondimensional parameters from the

governing difierential equations, consider a flow in which both viscosity and
gravity are important. An example of such a ftow is the motion of a ship,
where the drag experienced is caused both by the generation of surface waves
and by friction on the surface of the hull. AH other effects such as surface
tension and compressibility are neglected. The goveming differential equation
is the Navier-Stokes equation

6. Comments on Model Testing .... 257

Example 8.1 ................... 258

(1)

1. lntroduction
Two flows having difierent values of length scales, flow speeds, or fluid
propenies can be apparently diflerent, but still Udynamically similar." Exactly
what is meant by dynamic similarity will be explained later in the chapter. At
this point it is only necessary to know that, in a class of dynamically similar
flows, we can predict flow propenies if we have experimental data on one of
them. [n this chapter, we shall determine circumstances under which two tlows
can be dynamically similar to one another. We sha11 see that equality of cenain
relevant nondimensional parameters is a requirement for dynamic similarity.
What this nondimensional parameter should be depends on the nature of the
problem. For example, the nondimensional parameter must involve the fluid
viscosity if viscous eflects are important in the problem.
The principie of dynamic similarity iS..M..tbJLh~~.!U~J experimental fluid
mechanics, in which the data should be unified and presented in terms of
nondimensional parameters. The concept of similarity is also jndispensable
for designiOg models in which tests can be conducted for predicting flow
properties of full-scale objects such as aircraft, submarines, and dams. An
248

'.' 'f
I

tj
\
.

'" 1 .

\.
.... . ,t<.

,', L

XL.
1:'"

*- >.'
~.-T.
>i'-~" 1,. ::.

and two other equations for u and v. The equation can be nondimensionalized
by defining a characteristic length scale l and a characteristic velocity scale
U. In the present problem we can take l to be the length of the ship at the
waterline and U to be the free-stream velocity at a large distance from the
ship (Figure 8.1). The choice of these scales is, strictly speaking, arbitrary.
Dynamic similarity requires that the ftows have geometric similarity of the
boundaries, so that a11 characteristic lengths are proportional; for example, in
Figure 8.1 we must have dI 1= dll 11 , Dynamic similarity also requires that the
flows should be kinematically similar, that is they should have geometricaUy
similar streamlines. The velocities at the same relative location are therefore
proportional; if the velocity at point P in Figure 8.1a is U 12, then the velocity
at the corresponding point P t in Figure 8.lb must be U';2. AII length and
velocity sea les are then proportional in a class 01 dynamically similar flows. and
the specific choices 01 l and U are a malter 01 convenience and convenlion. For
example, we could take the characteristic length to be the depth d of the hull
under water. Such a choice is. however, unconventional. Moreover, a choice
of l as the length of the ship makes the nondimensional distances of interest
(that is the magnitude of xl l in the region around the ship) of order one.

D,'numic Sim ilurir,'

250

(b)

(,)

Fil:. 8.1

Two gc:ometric:lJly s imi l:l r ships.

S imil a rly, a cho ice o f U as th e frec -s tream ve loc ity makes the ma ximum va lu c
o f lhe nond imens io nal velocit y ul U of o rder o ne.
Acco rdingl y, \Ve introducc th e followi ng no nd imcn sio nal variables,
d en oled by prim es:
x

x'

y' =[

= =

v
v =V

w
)V' = -

"

"

t ,= tU

1
p' =

(2)

~ -,

tt is c1ea r that lhe bo undary co nditi o ns in terms of the no ndime n s io nal va ri ab les
in ( 2) a re ndepend ent 01" I a nd U. Fo r example, co nsider lhe visco us ft ow
over a ci rcul ar cylinder of radius R. We ch oose the ve locit y scale U 10 be ch e
rrec-st ream velocil Y and l he len gth scale 10 be lhe rad ius R. In tenn s of
nond ime ns ion a l vc loc it y 11 ' = ul U a nd lhe no ndimensio na[ coo rdin a te r' =
rl R. lhe bo undary co nditi on a l innic y is 11 ''''''' I as r' .... CO, and lhe eondition
at lhe s urfa ce o f lhe cy lin de r is u ' = O at r ' = 1.
No te Ihat no separate press urc sca le ha s been in troduced in (2). bcc:luse
in lhi s pro blem Ihe sca le for press ure ( n a m e ly pU!) is decided by rha t fo r
ve loc ic y, esse nliall y according to 8ernoull i's equat ion p + pU ~/ 2 = co ns tanl ,
which says th al a ve locilY c hange of U ca uses a pressu re c hange o f o rder
pU~ / 2. S u bs tiruli on o f ( 2) inl o (1 ) gives

aw' + " ,a\ll'

,aw' ,aw'
ap' gl v ( a~ w ' a!w' a~ w ' )
-+v - - +w - =- - - - + - - - + --+ - -

at'

dx '

ay'

az'

az'

u2

VI

ax,l

ay,2

a=,l

(3)

sam e nondi m ens iollal 501Ilt;0 I'lS.

The no nd ime ns io nal p arameters V II v and U l .fi have bee n give n s pecial
names:

Fr "

V
r- =

" gl

Fra ude nu mbe r

E.,ualio nJ

x)

p (x=
) [ ( Fe Re pV'
' 1

25 1

(4 )

(5 )

whe re p i pU 2 is ca Jl ed lhe pressZlre coefficie1l1. Sim ila r re la lio ns a[ so ho ld fo r

a ny othe r nondimens ionaJ now variab le s ue h as ve locit y ul U a nd acce lera tio n
2
'.111 U It foll o ws that in dyna mi ca ll y si milar ft ows the nondimen s io nal local
flow variables a re ide nt ical at correspondi"g po;ms (t hat is , fo r identical va lues
of xi i ).
In lhe fo rego ing analysis we ha ve assumed thar lhe imposed boundary
co nd itions are stead y. H oweve r, we ha ve ret:J.ine d lhe time deri v.ltive in (3)
beca use the res ulting ftow ca n s til\ be uns leady; ror eX:lmp le un Slable wa ves
ca n ari se s po ntan eo us ly under slead y bo und a ry eo ndirion s, 5uch un s le.ld in ess
mu st h ave a tim e scale pro po ni o nal to II U. as ass umed in (2 ). Ca nsi de r no\V
a s itu atio n in whic h {h e imposed bo unda ry co ndition s a re uns teady. To be
s pecific, co ns ider a n objecl ha vin g a characteris ti c length sca le I osci ll atin g
wil h a freq u ency w in a fluid a l rest at infinity. T h is is a pro bJem ha vin g an
imposed length sca le a nd an imposed (ime scale I l w. In s uch a case <1 ve loc it y
scale ca n be deri ve d fro m w .lnd I lO be U'"" lw. The preceding 3nalysis lhen
goc!s th ro ug h , leading la lhe co ncl usio n lhat Re = V II v = w l =1 v a nd Fr =
UI .Jii = w./TTi have to be duplicated for d y nami c si milarit y o f t\Vo fiows in
w hi ch vi sco us and gravitarional effects a re important.
AJI nondi m e ns iona l quantiti es a re identical for d ynamic.l ll y s imi lar flow s.
For ftow aro u nd an imme rsed body, we can d efi ne a no nd ime ns io nal dra g
coeffici ent
D

is appare nt that two fto ws ( ha vi ng differenl va lues of U , 1, o r v ), will obey

Ih e same nondim e nsio nal d iffere nt ia l cqua ti o n if the values of nond im cnsional
gro ups gil U!. a nd vi UI a re ide nli ca l. S in ce the no ndimen sio n a l boundary
condi tion s a re a lso identical in the t\Vo Aows. it fo llows lhat Ihey will lla ue rhe
[

VI
Re _ - = Rey n olds numbe r
v

DiJf~r",,.riaJ

l30th R.e a nd F r ha ve lo. be .equ a l fo r dyn amic s im ilarit y OflWO fl ow$ in w hich
both VISCO U S a nd gra vlla uon a l e fIects are imp ortan t. No te th at the me re
presence of grav ity do es n 't ~ak ~ the gravi tationa l e ffects dynamica ll y impo r.
ta ne For ftow aroun d an obJe cl In a ho m ogen eo us fluid , gravily is importaOl
o n ly if s urface wav.es a re generated. Ot h ~rw i se, the effecl of gravily is s ftlp ly
lO add a hyd rosla u c press ure 10 the entlre sys tem . whi ch ca n be elimi nat ed
by absorbi ng g ra vit y iOlo the pre$s ure tcrm.
Undcr d ynamic s irnil a rit y Ih e nondimen s ion a l so luti o ns are ide nti ca!.
T herefo re lhe local press u rc a r poi nt x = (x, y, z) mu st be 0 1' the form

~ l, --J

U,

Z. Nond;m ",nJ;Qna/ Parom",,..n Derennined f rom

CO IIii

~pU= , 2

( 6)

whcre D is lhe d rag expe ri enced by rhe bod y; u se 0 1' the factor o f 1/ 2 in (6)
is co n vent io nal b ut not necess ary. rnste.ld of writ ing Ca in lerm s o f a le ngt h
sca le 1, it is customary to d efi ne the drag coeffic ien t more gene raJl y as
D

eo . -!pU ~ A
w hc re A is a c ha racterislic arca. For blu nt bodies such as sp he res and cy linders,
A is take n to be a cross sectio n perpendicular to t he flow. T herefo re A = r.d 2 / 4
fo r a sp here of d iameler d, and A = bd fo r a cy Jind er of d iame ter d a nd le ngt h
b, the axi s of the cy linder be ing perpend ic ul a r to (h e flow. Fo r flow ove r a Rot

252

Dynamic SimilGrity

plate, on the otber hand, A is taken to be the "wetted area," that is A = bl

where / is the length of the plate in the direction of ftow and b is the width
perpendicular to the ftow.
The values of the drag coefficient C o are identical for dynamically similar
Oows. In the present example in which the drag is caused both by gravitational
and viscous effects, we must have a functional relation of the form

e o = f(Fr, Re)

(7)

For many ftows the gravitational effects are unimportant. An example is

the ftow around the body, such as an airfoil, that does not generate gravity
waves. In that case Fr is irrelevant, and
(8)

eo=f(Re)

4. BuckinghGm'$ Pi

253

11r~orem

The dimensions of the variables can be arranged in the form of the following
matrix:
tl.p

O O

-2

O O O

-1

3. Dimensional Matrix

f(tl.p, d, /, e, U, p, p.)

=O

(9)

1
-3

(lO)

-1

0-1

In the aboye, we have written the variables tlp, d,... on the top and their
dimensions in a vertical column undemeath. For example, [tlp] = ML -1,2.
An array of dimensions su eh as (lO) is called a dimensional malrix. The rank
r of any matrix is defined to be the size of the largest square submatrix that
has a nonzero determinant. Testing the determinant of the first three rows and
columns, we get
1

In many complicated ftow problems the precise form of the differential

equations may not be known. In this case the conditions for dynamic similarity
can be determined by means ofa dimensional analysis ofthe variables involved.
A formal method of dimensional analysis is presented in the following section.
Here we introduce certain ideas that are needed for performing a formal
dimensional analysis.
The underlying principie in dimensional analysis is that of dimensional
homogeneity, which states that all terms in an equation must have the same
dimensiono This is a basic check that we constantly apply when we derive an
equation; if the terms do not have the same dimension, then the equation is
not correcto
Fluid flow problems without electromagnetic forces and chemical reactions
involve only mechanical variables (such as velocity and density) and thermal
variables (such as temperature and specific heat). The dimensions of all these
variables can be expressed in terms of four basic dimensions: mass M, length
L, time T, and temperature 6. We shall denote the dimension of a variable q
by [q]. For example, the dimension of velocity is [u] = L/T, that of pressure
is [p]=[force]/[area]=MLT- 2/L 2 =M/LT2 , and that of specific heat is
[e] = [energy]/[mass][temperature] = MLT- 2 L/M6 = L2/6T2 When thermal
effects are not considered, all variables can be expressed in terms of three
fundamental dimensions, namely M, L, and T.
The m~thod of dimensional analysis presented here uses the idea of a
"dimensional matrix" and its rank. Consider the pressure drop tlp in a pipeline,
which is expected to depend on the inside diameter d of the pipe, its length
/, the average size e of the wall roughness elements, the average flow velocity
U, the fluid density p, and the fluid viscosity p.. We can write the functional
dependence as

-1

L
T

O O

-1

-2

O O

1 =0

However, there does exist a nonzero third-order determinant, for example the
one formed by the last three columns:

-3

-1

-1

=3

0-1

Thus, the rank of the dimensional matrix (10) is r = 3. If all possible third-order
determinants were zero, we would have concluded that r < 3 and proceeded
to test the second-order determinants.
It is clear that the rank is less than the number of rows only when one of
the rows can be obtained by a linear combination of the other rows. For
example, the matrix [not from (lO)]

[ -~
-1

1
2
4

has r = 2, since the last row can be obtained by adding the second row to twice
the first row. A rank of less than 3 commonly occurs in problems of statics,
in which the mass is really not relevant in the problem, although the dimensions
ofthe variables (such as force) involve M. In most problems in fluid mechanics
without thermal effects, r = 3.

4. Buckingham 's Pi Theorem

Of the various formal methods of dimensional analysis, the one that we shall
describe was proposed by Buckingham in 1914. Let q" q2, ... , qn be n variables
nvolved in a particular problem, so that there must exist a functional relation-

-" ",-

254

Dynamic Similariry

5. Nondimemional

Paramn~n

and Dynamic Similariry

255

ship of [he form

(11)

Buckingham's theorem states that the n variables can always be combined to

form exactly (n - r) independent nondimensional variables, where r is the rank
of Ihe dimensional malrix. Each nondimensional parameter is called a "n
number," or more commonly a nondimensional producto [The symbol rr is used
beca use the nondimensional parameter can be written as a product of the
variables ql"'" qn. raised to some power, as we shall see.] Thus (11) can be
written as a functional relationship

n 4 = UadbpCp. =~
pUd

Therefore, the nondimensional representation of the problem has the form

tlp
(1 e
.L)
pU 2 = 4> d' d' pUd

Other dimensionless products can be obtained by combining the four above.

For example, a group tlpd 2 pl p. 2 can be formed from nI/TI;. AIso, difierent
nondimensional groups would have been obtained had we taken variables
other than U, d, and p as the repeating variables. Whatever nondimensional
groups we obtain, only four of these are independent for the pipe flow problem
described by (13). However, the set in (14) contains the most commonly used
nondimensional parameters, which have familiar physical interpretation and
have been given special names. Several of the common dirnensionless
parameters will be discussed in Section 7.
The pi theorem is a formal method of forming dimensionless groups. With
sorne experience, it becomes quite easy to form the dimensionless numbers
by simple inspection. For example, since there are three length scales d, e,
and 1 in (13), we can form two groups such as el d and 1I d. We can also form
tlp/ pU 2 as our dependent nondimensional variable; the Bernoulli equation
tells us that pU 2 has the same units as p. The nondimensional number that
describes viscous effects is well-known to be pUdl p.. Therefore, with sorne
experience. we can find all the nondimensional variables by inspection alone,
and no formal analysis is needed.

(12)
It will be seen shortly that the nondimensional parameters are not unique.

However, (n - r) of them are independent and form a complete seto

The method of forming nondimensional parameters proposed by Buckingham is best illustrated by an example. Consider again the pipe flow problem,
expressed by
f(ilp. d, 1, e, U, P. p.) = O

(13)

whose dimensional matrix (10) has a rank of r = 3. Since there are n = 7

variables in the problem, the number of nondimensional parameters must be
n - r = 4. We first select any 3 (= r) of the variables as Urepeating variables,"
which we want to be repeated in all of our nondimensional parameters. These
repeating variables must ha ve different dimensions, and between them must
contain all the fundamental dimensions M, L. and T. In many fluid flow
problems we choose a characteristic velocity, a characteristic length. and a
fluid property as the repeating variables. For [he pipe flow problem. let us
choose U. d, and p as the repeating variables. Although other choices would
result in a difierent set of nondimensional products. we can always obtain
other complete sets by combining the ones we have. Therefore, any choice of
the repeating variables is satisfactory.
Each nondimensional product is formed by combining the three repeating
variables with one of the remaining variables. For example, let the first
dimensional product be taken as

ni =

ni =

5. Nondimensional Parameters and Dynamic Similarity

Arranging the variables in terms of dimensionless products is especially useful
in presenting experimental data. Consider the case of drag on a sphere of
diameter d moving at a speed U through a fluid of density p and viscosity .L.
The drag force can be written as

Uadbpc tlp

The exponents a. b. and c are obtained from the requirement that

dimensionless. This requires
MOL-Y-O = (LT-I)a(L)b(ML -3)'=(ML -'T- z) = M C -+- L a-+-b-3c- IT- a - Z
'
Equating indices, we get a = -2. b = O, e = -1, so that
U- 2 d O p- l tlp

rr

(14)

D =f(d, U, p, .L)

is

(l5)

If we do not form dimensionless groups, we would ha ve to conduct an

experiment to determine D versus d, keeping U, p, and p. fixed. We would
then have to conduct an experiment to determine D as a function of U, keeping
d, p, and p. fixed, and so on. However, such a duplication of effort is unnecessary
if we write (15) in terms of dimensionless groups. A dimensional analysis of
(15) gives

tlp
pU 2

~_f(PUd)
Z 2

A similar procedure gives

pU d

p.

(16)

reducing the number of variables from five to two, and consequently a single
-

256

Dynamic Similllrity

6. Commenrs

011

257

Model Tating

Prediction of Flow Behavior from Dimensional Considerations

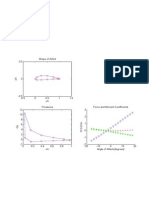
An interesting observation in Figure 8.2 is that Cooc l/Re at small Reynolds

100

e _

D-

tpU2A

numbers. This can be justified solely on dimensional grounds as follows. At

small values of Reynolds numbers we expect that the inertia forces in the
equations of motion must become negligible. Then p drops out of (15),
requiring

10

D=f(d, U,.t)
The only dimensionless product that can be formed from the abo ve is D/ .tUd.
Since there is no other nondimensional parameter on which D / .t Ud can
depend, it can only be a constant:
Doc.tUd
0.1

Fig.8.2 Orag coefficient for a sphere. The characteristic arca is taken as A = '1Td%/4. The reason
for the sudden drop of C o at Re- S x 105 is lhe transition of lhe laminar boundary layer lO a
turbulent one. as explained in Chapter 10.

experimental curve (Figure 8.2). Not only is the presentation of data united
and simplified, the cost of experimentation is drastically reduced. It is clear
that we need not vary the fluid viscosity or density at aH; we could obtain all
the data of Figure 8.2 in one wind tunnel experiment in which we determine
D for various values of U. If we want to find the drag force for a fluid of
difterent density or viscosity, we can still use Figure 8.2. Note that the Reynolds
number in (16) is written as the independent variable because it can be
extemally controlled in an experimento In contrast, the drag coefficient is
written as a dependent variable.
The idea of dimensionless products is intimately associated with the
concept of similarity. In fact, a collapse of all the data on a single graph such
as the one in Figure 8.2 is possible only because, in this problem, a11 flows
having the same value of Re = pUd/ .t are dynamically similar.
For flow around a sphere, the pressure at any point x = (x, y, z) can be
written as
p(x) =f(d, U, p, .t; x)

A dimensional analysis gives the local pressure coefficient:

p(x) =f(PUd;~)

pU 2

.t

(17)

requiring that nondimensional local ftow variables be identical at corresponding points in dynamically similar ftows. The difterence between relations (16)
and (17) should be noted. Equation (16) is a relation between overall quantities
(scales of motion), whereas (17) holds locally at a point.

(Re 1)

(18)

which is equivalent to Cooc l/Re. It is seen that the dragforce in a low Reynolds
number flow is linearly proporlional 10 the speed U; this is frequently called the
Stokes law 01 resistan ce.
At the opposite extreme, Figure 8.2 shows that C o becomes independent
of Re for values of Re> 103 This is because the drag is now mostly due to
the formation of a turbulent wake, in which the viscosity only has an indirect
inftuence on the ftow. [This will be c1ear in Chapter 12, where we shall see
that the only eftect of viscosity as Re ~ ce is to dissipate the turbulent kinetic
energy at increasingly smaller scales. The overall flow is controlled by inertia
forces alone.] In this limit .t drops out of (15), giving
D=f(d, U,p)
The only nondimensional product is then DI pU 2 d 2 , requiring
(Re 1)

(19)

which is equivalent to C o = constant. It is seen that the dragforce is proportional

lO U 2 for high Reynolds number flows. This rule is frequently applied to estimate
various kinds of wind forces such as those on industrial structures, houses,
automobiles, and the ocean surface.
It is clear that very useful relationships can be established based on sound
physical considerations, coupled with a dimensional analysis. In the present
case this procedure leads to DOC.tUd for low Reynolds numbers, and Doc
2
pU d 2 for high Reynolds numbers. Experiments can then be conducted to see
if these relations do hold, and to determine the unknown constants in these
relations. Such arguments are constantly used in complicated fluid flow problems like turbulence, where physical intuition plays a key role in research. A
well-known example of this is the Kolmogorov K- S/3 spectrallaw of isotropic
turbulence, presented in Chapter 12.

6. Comments on Model Testing

The concept of similarity is the basis of model testing, in which test data on
one ftow can be applied to other flows. The cost of experimentation with

258

Dynamic Similariry

full-scale objects (which are frequently called prototypes) can be greatly

reduced by experiments on a smaller geometrically similar model. Alternatively, experiments with a relatively inconvenient ftuid such as air or helium
can be substituted by an experiment with an easily workable ftuid such as
water. A model study is invariably undertaken when a new aircraft, ship,
submarine, or harbor is designed.
In many ftow situations both friction and gravity forces are important,
which requires that both the Reynolds number and the Froude number be
duplicated in a model testing. Since Re = UI/ v and Fr = U /.Jii, simultaneous
satisfaction of both criteria would require U ce 1/ I and U ce.Ji as the model
length is varied. It follows that both the Reynolds and the Froude numbers
cannot be simultaneously duplicated unless ftuids of diflerent viscosities are
used in the model and the prototype ftows. This becomes impractical, or even
impossible, since the requirement sometimes needs viscosities thal cannot be
met by common ftuids. It is then necessary to decide which of the two forces
is more important in the ftow, and a model is designed on the basis of the
corresponding dimensionless number. Corrections can then be applied to
account for the inequality of the remaining dimensionless group. This is
illustrated in Example 8.1, which follows this section.
Although geometric similarity is a precondition to dynamic similarity, this
is not always possible to attain. In a model study of a river basin, a geometrically
similar model results in a stream so shallow that capillary and viscous effects
beco me dominant. In such a case it is necessary to use a vertical scale larger
than the horizontal scale. Such distorted models lack complete similitude, and
their results are corrected before making predictions on the prototype.
Models of completely submerged objects are usually tested in a wind
tunnel or in a towing tank where they are dragged through a pool of water.
The towing tank is also used for testing models that are not completely
submerged, for example ship hulls~ these are towed along the free surface of
the Iiquid.

259

7. Signijicancf! 01 Common Nondimf!nsional Parameters

drag can be estimated by treating the surface of the hull as a ftat plate, for
which the drag coefficient C o is given in Figure 10.9 as a function of the
Reynolds number. Using a value of v = 10-6 m 2 /s for water, we get

VI/ v (model) = [2(100/25)]/10- 6 = 8 X 106

Ul/II (prototype)

= 10( 100)/10-6 =

109

For these values of Reynolds numbers, Figure 10.9 gives the frictional drag
coefficients of
C o (model) = 0.003

e o (prototype) = 0.0015
Using a value of P = 1000 kg/m 3 for water, we estimate
Frictional drag on model = !C O pV 2 A
= 0.5(0.003)(1000)(2)2(300/25 1) = 2.88 N
Out of the total model drag of 60 N, the wave drag is therefore 60 - 2.88 =
57.12 N.
Now the wave drag still obeys (20), which means that D/ pV 2 2 for the
two ftows are identical, where D represents wave drag alone. Therefore
Wave drag on prototype

= (Wave drag on model) (pp/ Pm)(/ p/ Im)2( U p/

= 57.12(1)(25)2(10/2)1 = 8.92 x lOs N

Vm ?

Having estimated the wave drag on the prototype, we proceed to determine

its frictional drago We get
Frictional drag on prototype = !Co pU 2 A
= (0.5)(0.0015)( 1000)( 10)1(300) = 0.225 x lOs N

Example 8.1
A ship 100 m long is expected to sail at 10 m/s. It has a submerged surface
of 300 m 2 Find the model speed for a 1/25 scale model, neglecting frictional
effects. The drag is measured to be 60 N when the model is tested in a towing
tank at the model speed. Based on this information estimate the prototype
drag, after making corrections for frictional effects.
Solution: We first estimate the model speed, neglecting frictional effects.
Then the nondimensional drag force depends only on the Froude number:
(20)
Equating Froude numbers for the model (denoted by subscript
prototype (denoted by subscript u p "), we get

Um

10

m") and

= UpJ gm/m/ gp/p = 10'1"1/25 = 2 mis

The total drag on the model was measured to be 60 N at this model speed.
Of the total measured drag, a part was due to frictional eflects. The frictional

Therefore
If we
measured
from (20)

total drag on prototype = (8.92 + 0.225) x 105 = 9.14 x lOs N.

did not correct for the frictional effects, and assumed that the
model drag was all due to wave effects, then we would have found
a prototype drag of

Dp = Dm(P p/ Pm)(/p / Im)2( U p / V m)1 = 60(1)(25)2(10/2)2 = 9.37 X 10 5 N

7. Significance 01 Common Nondimensional Parameters

So far we have encountered several nondimensional groups such as the pressure
coefficient p/ pU 2 , the drag coefficient D/2pU 2 / 2 , the Reynolds number Re =
UI/II, and the Froude number U /.Jii. Several independent nondimensional
parameters that commonly enter fluid flow problems are listed and briefly
discussed in this section. Other parameters will arise throughout the rest of
the book.

"'

260

O,.namic Simi14riry

Reynolds Number
The Reynolds number is the ratio of inertia force to viscous force:

which is analogous to
-p;lg(dp/ dz) 1 = N 2 L

au

Re

261

7. Significana of Common Nondimensional Parameren

g' = g(P2- PI)/ PI

since

(21)

is

similar

to

Richardson Number
Instead of defining the internal Froude number, it is more common to define
a nondimensional parameter that is equivalent to 1/Fr,2. This is called the
Richardson number, and in a two-Iayer situation it is defined as

Inertia force pu ax P U 2/ 1 UI
------oc--o
c ---., = Viscous force
a2 u J-LU /1- JI
J-L ax2

g'l
R i s -2

Equality of Re is a requirement for the dynamic similarity of ftows in which

viscous forces are important.

(22)

In a continuously stratified ftow, we can similarly define

Froude Number

The Froude number is defined as

Fr

Inertia force] 1/2

[ Gravity force
oc

[PU 1]
2

'Pi"""

1/2

2 [2

Ria--ur

= .g

(23)

It is clear that the Richardson numher has to be equal for the dynamic simiJarity
of two density stratified ftows.
Equations (22) and (23) define overaJl or bu/k Richardson numbers in
terms of the sea/es 1, N, and U. In addition, we can define a Richardson number
involving the local values of velocity gradient and stratification at a certain
depth z. This is caJled the gradient Riehardson number, defined as

Equality of Fr is a requirement for the dynamic similarity of ftows with a free

surface, in which gravity forces are dynamically significant. So me examples
of ftows in which gravity plays a significant role are the motion of a ship, ftow
in an open channel, and the flow of a liquid over the spi11way of a dam
(Figure 8.3).

Ri(z)

Internal Froude Number

In a density stratified fluid the gravity force can playa significant role without
the presence of a free surface. Then the etlective gravity force in a two-Iayer
situation is the Ubuoyancy" force (p'2 - PI) g, as seen in the preceding chapter.
In such a case we can define an internal Froude number as
Inertia force ]
Fr'a [
Buoyancy force

1/2

2
[PI U / [ ]
oc
(P2 - PI) g

1/2

U
=--

./i'i

Local Richardson numbers will be important in our studies of instability and

turbulence in stratified ftuids.

Mach Number
The Mach number is defined as

(21)

Inertia force
]
M == [ CompressibiJity force

where g' = g(P2 - PI)/ PI is the ureduced gravity." For a continuously stratified
fluid having a maximum buoyancy frequency N, we similarly define

[PU /IJ
2

1/2

oc

pc

2/

1/2

where c is the speed of sound. Equality of Mach numbers is a requirement

for the dynamic similarity of compressible ftows. For example. the drag
experienced by a body in a flow with compressibility etlects has the form

Fr'aM

Co=f(Re, M)
Flows in which M < 1 are called subsonic, whereas ftows in which M> 1 are
called supersonic. It will be shown in Chapter 15 that compressibility etlects
can be neglected if M < 0.3.
~
\

\_---- -,,
Ship

Fig. 8.3

Prandtl Number
The Prandtl number enters as a nondimensional parameter in ftows involving
heat conduction. It is defined as
Open channel

Spillway of dam

Pr

Examples of ftows in which gravity is important.

~~,~~ '.~.i

""'-

Momentum diffusivity
Heat ditlusivity

JI
J-L/ P
-;; = k/ pCp

Cp.L

=k

262

Dynamic: Similarity

Chapter 9

[t is therefore a fluid property and not a flow variable. For air at ordinary
temperatures and pressures Pr= 0.72, which is close to the value of 0.74
predicted from the kinetic theory of gases. For water at 20C, Pr = 7.1. Dynamic
similarity of flows involving thermal etIects requires equality of Prandtl
numbers.

'",

Exercises
1. Suppose that the power to drive a propeller of an airplane depends on
d (diameter of the. propeller), U (free-stream velocity), w (angular velocity
of propeller), e (velocity of sound), p (density of fluid), and .t. (viscosity).
Find the dimensionless groups. [n your opinion, which of these are the most
important and should be duplicated in a model testing?
2. A 1/25 scale model of a submarine is being tested in a wind tunnel, in
which p = 200 kPa and T = 300 K. If the prototype speed is 30 km/hr, what
should be the free-stream velocity in the wind tunnel? What is the drag ratio?
Assume that the submarine would not operate near the free surface ofthe ocean.

41

Laminar Flow
1. Introduction .................. 263
2. Analogy between Heat and Vorticity
Diffusion .................... 265
J. Pressure Change Due 10 Dynamic
Effects. . . . . . . . . . . . . . . . . . . . . .. 265
4. Steady Flow between Parallel
Piares . ...................... 266
Planc Couette Aow . . . . . . . . . . . .. 268
Plane Poiseuille Aow ........ . .. 269.
5. Steady Flow in a Pipe. . . . . . . . .. 270
6. Steady Flow between Concentric
Cylinders . . . . . . . . . . . . . . . . . . .. 271
Aow Outside a Cylinder Rotating in an
lnnite Auid . . . . . . . . . . . . . . .. 272
Aow lnside a Rotating Cylinder . .. 273
.7. Impulsively Started Plate: Similarity
Solutions .................... 274
Formulation of a Problem in Similarity
Variables ................... 274

Similarity Solution . . . . . . . . . . .. 277

An Alternative Method of Deducing the
Form of TI ................. 279
Method of Laplace Transform . . .. 280
8. Diffusion 01 a Vortex Sheet . . .. 280
9. Decay 01 a Une Vortex ... . . .. 282
10. Flow Due ro an Oscillaring

Plate ....................... 284

11. High and Low Reynolds Number

Flows ...................... 287

12. Creeping Flow around a

Sphere ...................... 289

01 Slokes's SoIurion
and Oseen's Improvement ..... 292
14. Final Remarks. . . . . . . . . . . . . .. 296
Exercises. . . . . . . . . . . . . . . . . . .. 296
Uterature Cited. . . . . . . . . . . . .. 298
Supplemental Reading
298
13. Non un iform ity

1. lntroduction
In Chapters 6 and 7 we studied inviscid flows, in which the viscous terms in
the Navier-Stokes equations were dropped. The underlying assumption was
that the viscous forces were confined to thin boundary layers nearsolid surfaces,
so that the bulk of the flow could be regarded as inviscid (Figure 6.1). We
shall see in the next chapter that this is indeed valid if the Reynolds number
is large. For low values of the Reynolds number, however, the entire flow may
be dominated by viscosity, and the inviscid fiow theory is of liule use. The
purpose of this chapter is to present certain solutions of the Navier-Stokes
equations in sorne simple situations, retaining the viscous term p. V 2 u
263