O VOLUME EXATO DA CUNHA ESFRICA E A INTEGRAL TRIPLA

Marcelo M. Lapola, Vinicius Barros e Gabriel Jorge

Departamento de Fsica Unesp - Universidade Estadual Paulista
Julio de Mesquita FilhoRio Claro, SP, Brasil
(15 de Janeiro 2015)
Neste trabalho revisamos os conceitos utilizados no Clculo Diferencial e Integral para a
obteno de uma frmula geral para o clculo da integral tripla de funes em coordenadas esfricas.
Para isto, estabelecemos a forma do elemento infinitesimal de volume em coordenadas esfricas a
partir de uma cunha esfrica obtida como elemento fundamental de uma partio definida neste
sistema de coordenadas.

I.

Introduo

A necessidade de se calcular reas de

determinadas regies, limitadas por curvas nos
levou definio de integral definida. Para o
clculo do volume de um slido, gerado por
funes de duas ou trs variveis, nos utilizamos
das integrais mltiplas. So semelhantes os
procedimentos para a definio, em especial da
integral tripla para o clculo do volume de slidos
gerados por uma regio determinada. Para a
demonstrao da frmula geral da integral tripla
em coordenadas esfricas seguimos o roteiro
estabelecido pelo exerccio de nmero 45
proposto por James Stewart no captulo 15 do
segundo volume de seu livro intitulado Clculo
(editora Cengage Leraning sexta edio).
Dividido em trs partes, a soluo de tal problema
nos leva a demonstrao de que o elemento
infinitesimal de volume para a integral tripla em
coordenadas esfricas dado por
, onde (,
= 2
, )
algum ponto do interior de uma regio que
definiremos como uma cunha esfrica.
Para chegarmos a este resultado, conforme
proposto
pelo
problema
supracitado,
primeiramente calcularemos o volume de um
slido limitado por cima por uma esfera e por
baixo por um cone, com intervalos de variao
definidos, usando para isso coordenadas
cilndricas
.
Deduzida a frmula do volume desta regio
partimos para a segunda parte do problema que
a deduo do volume de uma cunha esfrica, em
coordenadas esfricas, a partir da frmula do
volume do cone obtida na primeira parte. Por fim,
na ltima parte do exerccio, aplicamos o
Teorema do Valor Mdio para mostrar que o
volume pode ser dado pela frmula citada.
Antes de descrever e resolver o problema vamos
revisar alguns conceitos, como coordenadas

cilndricas e esfricas, bem como a ideia de

partio e soma de Riemann para o Clculo das
integrais mltiplas.
II . Coordenadas cilndricas e esfricas e suas
transformaes retangulares no espao
euclidiano
No espao euclidiano tridimensional, onde valem
os conceitos de geometria plana, temos dois
sistemas de coordenadas que nos fornecem uma
maneira mais conveniente para descrever de
modo mais simples algumas curvas, superfcies e
slidos. So as coordenadas cilndricas e as
esfricas.
No sistema de coordenadas cilndricas, um ponto
P qualquer dado por uma tripla ordenada (r,, ),
onde r e so as coordenadas polares da projeo
de P no plano xy e z a distncia orientada do
plano xy at z, conforme mostrado na figura 1.
A transformao de coordenadas cilndricas em
retangulares dada pelas equaes:
x = r cos y = r sen z = z

(1)

Para o caminho inverso, isto , a converso de

coordenadas retangulares para cilndricas,
usamos:
2 = 2 + 2 ; =

;z=z

(2)

Usamos as equaes de transformao para

converter de coordenadas esfricas para
coordenadas retangulares e vice-versa.
Muitos problemas de integrais duplas, por conta
de sua simetria, tem sua resoluo facilitada
quando o tratamos em um sistema de coordenadas
esfricas.

II.

De maneira anloga a definio de integrais em

uma dimenso o para funes de uma s varivel
e integrais duplas para as funes de duas
variveis, as integrais triplas so definidas para
funes de trs variveis. De incio trata-se do
problema mais simples, definindo-a em uma
regio do espao em formato de uma caixa
retangular (Fig 3) do tipo:

Fig. 1: O sistema de coordenadas cilndricas

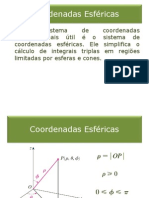
As coordenadas esfricas de (, , ) de um
ponto P qualquer (Fig. 2) esto relacionadas s
coordenadas
cartesianas
pelas
seguintes
transformaes:
= sin ; y = sin sin
(3)
z= cos
Alm disso, temos tambm a seguinte frmula
para a distncia.
2 = 2 + 2 + 2

A INTEGRAL TRIPLA

(4)

= {(, , )| , , } (5)

Como primeiro passo, dividimos B em subcaixas.

Com isso, dividiremos [a, b] em subintervalos
[1 , ] de comprimentos iguais , dividido [c,
d] em m subintervalos de comprimento , e o
intervalo [r, s] em n subintervalos de
comprimento .
Assim temos as subcaixas
= [1 , ] [1 , ] [1 , ]

(6)

Como mostrado na Fig. 3, cada subcaixa tem o

volume = .
Desse modo podemos formar uma soma tripla de
Riemann:

=1
=1 =1 ( )

(7)

onde (

) o ponto amostral em .

Analogamente a definio de integral dupla,

definimos a integral tripla como o limite da soma
tripla de Riemann em (7):

Fig. 2: Sistema de coordenadas esfricas

(, , ) = lim (

)
,,

se o limite existir.

=1 =1 =1

(8)

O limite existe se f (x, y, z) contnua em B

Em regies limitadas por cones e esferas, o
clculo da integral tripla simplificado se o
problema for tratado em coordenadas
esfricas. Neste sistema, o correspondente
caixa retangular a cunha esfrica (Fig 4).
E = {( , , )| , , }

(10)

Fig. 4 A cunha esfrica.

A Fig 4 mostra que E aproximadamente

uma caixa retangular de dimenses ,
(arco de circunferncia de raio e ngulo
) ) e . Logo uma aproximao
do volume de pode ser escrita como:
= ()( ) = 2

(11)

Fig 3 e 3.1 Partio de uma caixa retangular em

subcaixas de volume .

Resta, ento provar, com a ajuda do Teorema

do Valor Mdio que o valor exato do volume
de dado por:

= 2

Ento, de acordo com o Teorema de Fubini:

(, , ) = (, , )
(9)
Os elementos diferenciais na integral do lado
direito do Teorema de Fubini indicam a ordem de
integrao.
III.

A CUNHA ESFRICA

(12)

conforme citado na introduo deste artigo.

Para isso seguiremos o roteiro estabelecido
no tambm j citado exerccio proposto e ao
final provaremos a relao.

IV.

DO VOLUME DO
CONE AO
VOLUME DA CUNHA ESFRICA

Primeiramente, no caminho para estabelecer a Eq.

(11) vamos calcular, conforme proposto no citado
exerccio o volume do slido limitado por cima
pela esfera 2 + 2 = 2 e por baixo pelo cone
= cot 0 (ou 0 = ) , onde 0 < 0 < /2 .
Para encontrar este volume utilizaremos
coordenadas cilndricas. Na regio delimitada
pelos slidos citados acima temos o volume
= (13)
sobre esta regio que passamos a chamar de D.
Substituindo o cone na equao da esfera, temos
2 + ( cot ) 2 = 2
o que nos leva a

(14)

= 2 / csc 2

(15)

23
3

(1 cos )

Assim,
=

23
3

(1 cos )

(19)

Na segunda parte do problema utilizamos o

resultado obtido na Eq.(19) para o clculo do
volume de uma cunha esfrica.

Eliminando a raiz r variar de zero a

= sin

(16)

Ento a variao de z ser

= cot
(17)

= 2 2

Por fim a variao de ser de zero a 2. Com

isso, temos que o volume do cone ser dado por:
2

sin

0 0
2

2 2

cot

sin

= 0 0

(18)

[(2 2 ) cot ]

Calculando a segunda integral iterada em dr

sin

sin

2 2

cot

3
= (1 )
3
Resultado que foi encontrado aps substituio de
variveis e o clculo da integral nos limites
estabelecidos.
Por fim, o clculo da terceira integral iterada (em
), chegamos equao do volume do cone.
2

3
(1 )
3

Fig 4.1 Cunha esfrica (Exemplificao)

A partir da figura acima e uma vez assumidas as
seguintes afirmaes:
1 2

1 2 ; 1 2

Segue:
1 =

1 1 3
(1 cos 1 )
3

2 =

2 2 3
(1 cos 2 )
3

2 1 =

2 2 3
1 1 3
(1 cos 2 )
(1 cos 1 )
3
3

= (2 1 )(2 3 1 3 )(1 cos 2 ) (c)

3

Pelo teomera do valor intermedirio, observamos:

 () =

() ()

Considerando () = 3 existir entre [2 , 1 ]

de tal maneira que:
32 = 23 13 (a)
Por sua vez, adotando: () = cos() e
aplicando o teorema do valor intermedirio de
forma anloga ao caso anterior, chegamos:
) = cos(1 2 ) (b)
sin(
Substituindo (a) e (b) em (c):
1
= (2 3 1 3 )(cos(1 ) cos(2 ))(2 1 )
3

Simplificando e reescrevendo a expresso,

finalmente concluimos que:
)
2 sin(
=