1

Lecture Notes on Fluid Dynamics

(1.63J/2.21J)
by Chiang C. Mei, MIT
2007 Spring
2-5Stokes.tex
2.5 Stokes ow past a sphere
[Refs]
Lamb: Hydrodynamics
Acheson : Elementary Fluid Dynamics, p. 223
One of the fundamental results in low Reynolds-number hydrodynamics is the Stokes so-
lution for steady ow past a small sphere. Applications range widely from the determination
of electron charges to the physics of aerosols.
The continuity equation reads
q = 0 (2.5.1)
With inertia neglected, the approximate momentum equation is
0 =
p

+
2
q (2.5.2)
Physically, the presssure gradient drives the ow by overcoming viscous resistence, but does
aect the uid inertia signicantly.
Refering to Figure 2.5 for the spherical coordinate system (r, , ). Let the ambient
velocity be upward and along the polar (z) axis: (u, v, w) = (0, 0, W). Axial symmetry
demands

= 0, and q = (q
r
(r, ), q

(r, ), 0)
Using a known formula for the divergence in spherical polar coordinates, Eq. (2.5.1) becomes
1
r
2

r
(r
2
q
r
) +
1
r sin

(q

sin ) = 0 (2.5.3)
An equivalent and physically more revealing way is to write

r
(r
2
q
r
sin ) +

(rq

sin ) = 0 (2.5.4)
As in the case of rectangular coordinates, we dene the stream function to satisify the
continuity equation (2.5.4) identically
q
r
=
1
r
2
sin

, q

=
1
r sin

r
(2.5.5)
2
z
y
x
r
o
f
q
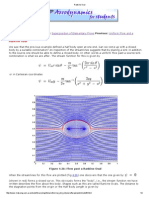
Figure 2.5.1: The spherical coordinates
At innity, the uniform velocity W along z axis can be decomposed into radial and polar
components
q
r
= W cos =
1
r
2
sin

, q

= W sin =
1
r sin

r
, r (2.5.6)
The corresponding stream function at innity follows by integration
=
W
2
r
2
sin
2
, r (2.5.7)
Using the vector identity
(q) = ( q)
2
q (2.5.8)
and (2.5.1), we get

2
q = (q) =

(2.5.9)
Taking the curl of (2.5.2) and using (2.5.9) we get
(

) = 0 (2.5.10)
After some straightforward algebra given in the Appendix, we can show that
q =
_
e

r sin
_
(2.5.11)
and

= q =
_
e

r sin
_
=
e

r sin
_

r
2
+
sin
r
2

_
1
sin

__
(2.5.12)
3
Now from (2.5.10)
(q) =
_

r sin
__
= 0
hence, the momentum equation (2.5.10) becomes a scalar equation for .
_

2
r
2
+
sin
r
2

_
1
sin

__
2
= 0 (2.5.13)
The boundary conditions on the sphere are
q
r
= 0 q

= 0 on r = a (2.5.14)
The boundary conditions at is

W
2
r
2
sin
2
(2.5.15)
Let us try a solution of the form:
(r, ) = f(r) sin
2
(2.5.16)
then f is governed by the equi-dimensional dierential equation:
_
d
2
dr
2

2
r
2
_
2
f = 0 (2.5.17)
whose solutions are of the form f(r) r
n
, It is easy to verify that n = 1, 1, 2, 4 so that
f(r) =
A
r
+ Br + Cr
2
+ Dr
4
or
= sin
2

_
A
r
+ Br + Cr
2
+ Dr
4
_
To satisfy (2.5.15) we set D = 0, C = W/2. To satisfy (2.5.14) we use (2.5.5) to get
q
r
= 0 =
W
2
+
A
a
3
+
B
a
= 0, q

= 0 = W
A
a
3
+
B
a
= 0
Hence
A =
1
4
Wa
3
, B =
3
4
Wa
Finally the stream function is
=
W
2
_
r
2
+
a
3
2r

3ar
2
_
sin
2
(2.5.18)
4
Inside the parentheses, the rst term corresponds to the uniform ow, and the second term
to the doublet; together they represent an inviscid ow past a sphere. The third term is
called the Stokeslet, representing the viscous correction.
The velocity components in the uid are: (cf. (2.5.5) :
q
r
= W cos
_
1 +
a
3
2r
3

3a
2r
_
(2.5.19)
q

= W sin
_
1
a
3
4r
3

3a
4r
_
(2.5.20)
2.5.1 Physical Deductions
1. Streamlines: With respect to the the equator along = /2, cos and q
r
are odd while
sin and q

are even. Hence the streamlines (velocity vectors) are symmetric fore and
aft.
2. Vorticity:

=
_
1
r
(rq

)
r

1
r
q
r

_
e

=
3
2
Wa
sin
r
2
e

3. Pressure : From the r-component of momentum equation

p
r
=
Wa
r
3
cos (= (q))
Integrating with respect to r from r to , we get
p = p

3
2
Wa
r
3
cos (2.5.21)
4. Stresses and strains:
1
2
e
rr
=
q
r
r
= W cos
_
3a
2r
2

3a
3
2r
4
_
On the sphere, r = a, e
rr
= 0 hence
rr
= 0 and

rr
= p +
rr
= p

+
3
2
W
a
cos (2.5.22)
On the other hand
e
r
= r

r
_
q

r
_
+
1
r
q
r

=
3
2
Wa
3
r
4
sin
Hence at r = a:

r
=
r
= e
r
=
3
2
W
a
sin (2.5.23)
5
The resultant stress on the sphere is parallel to the z axis.

z
=
rr
cos
r
sin = p

cos +
3
2
W
a
The constant part exerts a net drag in z direction
D =
_
2
o
ad
_

o
d sin
z
==
3
2
W
a
4a
2
= 6Wa (2.5.24)
This is the celebrated Stokes formula.
A drag coecient can be dened as
C
D
=
D
1
2
W
2
a
2
=
6Wa
1
2
W
2
a
2
=
24
W(2a)

=
24
Re
d
(2.5.25)
5. Fall velocity of a particle through a uid. Equating the drag and the buoyant weight
of the eparticle
6W
o
a =
4
3
a
3
(
s

f
)g
hence
W
o
=
2
9
g
_
a
2

f
_
= 217.8
_
a
2

f
_
in cgs units. For a sand grain in water,

f
=
2.5 1
1
= 1.5, = 10
2
cm
2
/s
W
o
= 32, 670 a
2
cm/s (2.5.26)
To have some quantitative ideas, let us consider two sand of two sizes :
a = 10
2
cm = 10
4
m : W
o
= 3.27cm/s;
a = 10
3
cm = 10
5
= 10m, W
o
= 0.0327cm/s = 117cm/hr
For a water droplet in air,

f
=
1
10
3
= 10
3
, = 0.15 cm
2
/sec
then
W
o
=
(217.8)10
3
0.15
a
2
(2.5.27)
in cgs units. If a = 10
3
cm = 10m, then W
o
= 1.452 cm/sec.
6
Details of derivation
Details of (2.5.11).
q =
_

r sin
e

_
=
1
r
2
sin

e
r
e

r sin e

0 0

= e
r
_
1
r
2
sin

_
e

_
1
r sin

r
_
Details of (2.5.12).
q =
_

r sin
_
=
1
r
2
sin

e
r
re

r sin e

1
r
2
sin

1
sin

r
0

=
e

r sin
_

r
2
+
sin
r
2

_
1
sin

__