M3L1

Concept and Definitions of Random Variables

1. Introduction
This is the first lecture on random variables. In this lecture, the basic concept of random
variable, its definition, different types of random variables, their probability distribution and
properties etc. are discussed.
2. Concept of Random Variable
Concept of Random Variable (RV) is most important to the probability theory and its
applications. It is critical to always remember that: a Random Variable is not a variable.
According to classical concept, a random variable is a function denoted by or , that
map each points (outcomes of an experiment) over a sample space to a numerical value on
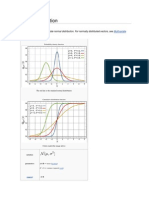
the real line. The Fig. 1. provides the visualization of this concept.

Fig. 1. Random Variable
Notations: Generally a Random Variable is denoted as, uppercase letter and its specific
values are denoted as lowercase letters. Thus, or denotes the RV and x denotes a
specific value of it.

Examples:
a. Number of rainy days in a month. Suppose, it is denoted by D . Some value of D, say
5, indicates 5 rainy days are observed in a particular month. Here D is the random
variable and d = 5.
b. Number of road accidents along a particular stretch of a road in a year. Suppose, it is
denoted by X. Some value of X, such as, x = 10 indicates 10 road accidents over that
stretch of road has occurred in a particular year.
Sample space

c. Strength of concrete. Suppose it is denoted by C . Some value of C, such as,

c = 25 N/mm
2
, indicates 25 N/mm
2
strength was observed for particular sample of
concrete.
3. Definition of Random Variable (RV)
Random Variable: A random variable X is a process to assign a number to every
outcome of a random experiment. The resulting function must satisfy following two
conditions
a. the set is an event for every .
b. the probabilities of the events and are equal to zero.
If not explicitly stated, all random variables are real.
4. Types of Random Variables (RVs)
There can be three possible types of RVs depending on the possible set of values.
4.1. Discrete Random Variable: If the possible set of values that a Random Variable is
assigned with some probability is finite, the random variable is called as Discrete Random
Variable. For Discrete Random Variable, all the probabilities, assigned at specific values, are
greater than or equal to zero. Summation of these probabilities for all possible values is
equal to 1.
Example 1. The number of rainy days at a particular location over a period of one month.
Example 2. Number of road accidents over a particular stretch of a national highway during a
year.
Example 3. Traffic volume at a particular section of a road.
4.2. Continuous Random Variable: If the possible set of values is a range (not discrete
values) over which the probability of a Random Variable is defined, then the random variable
is called as Continuous Random Variable. For Continuous Random Variable, probability of
any specific value is zero, however the probability of any infinitesimally small set of values is
greater than or equal to zero and the integration of the entire area under the curve on the
random variable axis is equal to 1.
Example 1. The amount of rain received at a particular place over a period of one year.
Example 2. Compressive strength of a concrete cube.
4.3. Mixed Random Variable: If some range of possible set of values of a Random Variable is
discrete and for the other range of possible set is continuous, then the random variable is
called as Mixed Random Variable.

Example 1. Depth of rainfall at a particular rainguage station. There can be some fixed
probability for zero values, which can be defined by a concentrated probability value. For
other range (greater than zero), probability can be defined by a continuous probability density
function. Thus, the random variable for records of depth of rainfall is a mixed type.
5. Special Type of Random Variables
There is a special type of Random Variable beyond the three defined before. It deals with
occurrence of event following a particular condition. This is known as, Indicator Random
Variable. It is a special kind of Random Variable associated with occurrence of an event. An
Indicator Random Variable, I
A
represents all the outcomes in the set A as 1 and all the
outcomes outside A are 0.
6. Independence of Random Variables
Two Random Variables, R
1
and R
2
are independent if for all , there exist the
condition that, .
Random Variables R
1
, R
2
, R
3
,..., R
t
are mutually independent if for all , there
exist the condition that, .
A collection of Random Variables are said to k-wise independent if all the subsets of k-
variables are mutually independent.
When the number of variables reduced to 2 and if the subsets are mutually independent, the
random variables are said to be pair-wise independent.
7. Probability Distribution of Random Variables
The distribution function of Random Variable, X is the function for any x
between and . In the subsequent lectures, we will differentiate between probability
density function (pdf) and cumulative distribution function (CDF). In this section we mean
CDF by Probability Distribution.
7.1. General notation: Distribution function of X, Y, and are denoted by
, , respectively. Variables x ,y, z (inside the parenthesis can be denoted by
any letter.
This is also known as, Cumulative Distribution Function (CDF). This will be discussed along
with probability density function (pdf) later.
7.2. Probability Distribution of different Random Variables
Probability distributions for various types of Random Variable are classified following their
properties.

7.2.1. Discrete Probability Distribution: It is a mathematical function (denoted as p(x) ) that

satisfies the following properties:
a. The probability of any event x can take a specific value p(x) , mathematically denoted as,
.
b. p(x) is non-negative for all real .
c. The sum of p(x) over all possible values of x is 1.
Though mathematically there is no restriction, in practice, discrete probability distribution
function is defined only for integer values.
7.2.2. Continuous Probability Distribution: It is a mathematical function (denoted as F
x
(x) )
that satisfies the following properties:
a. For all x,
b. It is monotonically increasing continuous function
c. It is 1 at and 0 at , i.e. and .
7.2.3. Mixed Probability Distribution: It is mathematical function (denoted as F
x
(x)) that
satisfies the following properties:
a. For all x,
b. It is monotonically increasing continuous function with sudden jumps or steps
c. It is 1 at and 0 at , i.e. and .
7.3. Usage in Statistics
There are several applications of concept of Random Variable and its probability distribution
in the field of statistics, viz. to calculate intervals for parameters and to calculate critical
regions, to determine reasonable distributional model for univariate data, to verify
distributional assumptions, to study the simulation of random numbers generated from a
specific probability distribution etc.
7.4. Usage in Civil Engineering
In Civil Engineering, concept of Random Variable and its probability distribution are used in
numerous applications. Here are some examples in different subfields of Civil Engineering:
in Water Resources Engineering: Analysis of flood frequency; Next in Geotechnical
Engineering: Distribution of in-situ stresses in rock surrounding an opening, uniaxial
compressive strength etc.; then in Structural Engineering: Distribution of damage stress in
masonry structure etc. to check seismic vulnerability; further in Transportation Engineering:
Traffic volume analysis etc.

7.5. Percentiles of Random Variables

The u-percentile of a Random Variable is the smallest number x
u
so that
. Where, x
u
is the inverse of the distribution function Fx (x) , i.e.
within the domain and the range of being .
7.6. Properties of Distribution Functions
Notations: , where .
Property 1. , .
We can prove this property in the following way:
and .
Property 2. F(X) is a non-descending function of X , if x
1
< x
2
, then .
We can prove this property in the following way:
Since and for some , is a subset of the event .
Hence . Here F(X) increases from 0 to 1 as x increases from to
.
Property 3. If , then for any .
We can prove this property in the following way:
Since (from previous proof), and suppose that for every . Again,
since is an impossible event. So, for each .
Property 4.
We can prove this property in the following way:
The events and are mutually exclusive and . So,
, then , .
Property 5.The function F(x) is continuous from the right: F(x
+
)=F(x).
We can prove this property in the following way:
Since, and when as
.
Property 6.

We can prove this property in the following way:

and are mutually exclusive and
again, . So,
or
.
Property 7.
We can prove this property in the following way:
Putting and in Property 6, we get,
. Now taking ,

Property 8.
We can prove this property in the following way:
Using Property 6 and 7, we get, and since
and are mutually exclusive events,

or
or
8. Concluding Remarks
Random Variable is not a variable, rather a function which maps all the feasible outcome of
an experiment on the real line or a set of real numbers. Random Variables can be either
discrete or continuous if the set of events defined by variable is either finite or infinite
numbers respectively. Mixed Random Variables are the combination of the both. It is also
true for probability distributions of them. Concept of Random Variable and its distributions
have numerous specific applications in Civil Engineering related problems. These problems
will be discussed in following lectures.