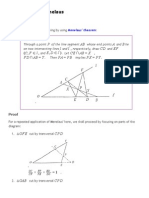
A Better Butterfly Theorem

The following generalization of the Butterfly Problem has been pointed out to me by Qiu
Fawen, a Chinese teacher who discovered the result with his students in 1997. The Chinese
version was at sime time available at qiusir.com. I had to do some guess work to figure out
what it was about.
According to Leon Bankoff (Mathematics Magazine, Volume 60, No. 4, October 1987, pp. 195-
210) the appellation The Butterfly made its first appearance in the Solutions section of
the American Mathematical Monthly in the February 1944 issue. Since the diagram of the
theorem (with two wings on each side) established by Qiu Fawen and his students gives a
more realistic depiction of a butterfly, I suggest to call the statement A Better Butterfly
Theorem which might be interpreted as both A "Better Butterfly" Theorem and A Better
"Butterfly Theorem", the former being my preference.
A Better Butterfly Theorem
Let there be two concentric circles with the common center O. A line
crosses the two circles at points P, Q and P', Q', M being the common
midpoint of PQ and P'Q'. Through M, draw two lines AA'B'B and CC'D'D and
connect AD', A'D, BC', and B'C. (This is the Butterfly.) Let X, Y, Z, W be
the points of intersection of PP'Q'Q with AD', B'C, A'D, and BC',
respectively. Then
(1) 1/MX + 1/MZ = 1/MY + 1/MW.
(Since X coincides with Z and Y with W when the two circles coalesce into one, The
Butterfly Theorem is an immediate consequence of A Better Butterfly Theorem.)
The proof depends on the following
Lemma
Let in RST, RU be a cevian through vertex R. Introduce angles a = SRU
and b = URT. Then
(2) sin(a + b)/RU = sin(a)/RT + sin(b)/RS.
The proof follows from the fact that Area( RST) = Area( RSU) + Area( RUT) by a consistent
application of the sine formula for the area of a triangle. (For
example,Area( RST) = RSRTsin(a + b)/2.)
Proof of the theorem
We apply Lemma to triangles AMD', A'MD, B'MC, and BMC':
(3)
sin(a + b)/MX = sin(a)/MD' + sin(b)/MA,
sin(a + b)/MZ = sin(a)/MD + sin(b)/MA',
sin(a + b)/MY = sin(a)/MC + sin(b)/MB',
sin(a + b)/MW = sin(a)/MC' + sin(b)/MB.
In view of (3), (1) will follow from
(4)
sin(a)/MD' + sin(b)/MA + sin(a)/MD + sin(b)/MA' =
sin(a)/MC + sin(b)/MB' + sin(a)/MC' + sin(b)/MB,
or, which is the same, from
(5)
sin(b)(1/MA - 1/MB) + sin(b)(1/MA' - 1/MB') =
sin(a)(1/MC - 1/MD) + sin(a)(1/MC' - 1/MD').
Now, drop perpendiculars OM
1
and OM
2
from O onto AA'B'B and CC'D'D. M
1
is the midpoint of
both AB and A'B', whereas M
2
is the midpoint of CD and C'D'. Obviously,
(6)
MB - MA = MB' - MA' = 2OM
1
= 2OMsin(a) and
MD - MC = MD' - MC' = 2OM
2
= 2OMsin(b).
With (6) in mind, (5) is equivalent to
(7) 1/MAMB + 1/MA'MB' = 1/MCMD + 1/MC'MD'.
However, as is well known, MAMB = MCMD and MA'MB' = MC'MD'. Therefore, (7) is true, as
is (5), which in turn, implies (1).