Documenti di Didattica
Documenti di Professioni
Documenti di Cultura
Theory
Caricato da
Ankur GhoshDescrizione originale:
Copyright
Formati disponibili
Condividi questo documento
Condividi o incorpora il documento
Hai trovato utile questo documento?
Questo contenuto è inappropriato?
Segnala questo documentoCopyright:
Formati disponibili
Theory
Caricato da
Ankur GhoshCopyright:
Formati disponibili
THEORY
4. Governing Dynamic Equations:
Unlike the case of a rigid body, only Newtons second law of motion is not sufficient to derive
the laws of motion for a deformable continuum. Here, the governing equation for an elastic body,
subjected to time-dependent loading, is derived from the dAlemberts principle, which is an
alternative way to express the Newtons second law of motion, written as follows:
(1)
where, the vector is considered to be an inertial pseudo-force, is the force acting on the
mass m, while a is the acceleration of the mass, with the result that the above equation assumes a
look similar to the equation of statics. For a deformable continuum,
the inertia force is
and is a distributed body force by nature. Here ,
, V and t signifies mass
density, displacement of the mass, volume and time variable,
respectively. The following
relation, derived from the principle of virtual displacement,
(2)
is also a valid equation of static equilibrium and may be generalised to include the
dynamic
conditions by adding the integral
to the left-hand side
of Eq. (2).
Variables B and T stand for the body force and the traction force on volume V and surface S
respectively, and stand for strain and stress, respectively, while is the variation symbol.
Thus at time t for a virtual displacement field u
i
, consistent with the constraint conditions
present, the relation can be extended as follows
(3)
This is a statement of the principle of virtual work, with inertia included as a distributed body
force. In general, the displacement vector at a point has six components or displacement degrees
of freedom
(4)
Thus Eq. (2.2.3) can be rewritten in the matrix form as follows:
(5)
The structural displacement at any point on the domain could be approximated as
(6)
where, {d} is an array containing displacements at certain predefined points on the structure,
called nodes, [N] is an array of interpolation functions, and {u}is the array of displacements at
any desired point on the structure, interpolated from the nodal displacements. The interpolation
functions, [N], are assumed to be spatial functions whereas the nodal displacements, {d}, are
temporal functions. Terms in Eq. (6) can be spatially differentiated to obtain strain versus nodal
displacement relation, given by
{} = [B]{d} (7)
The constitutive relation may be written as
{} = [D]{} (8)
The detail expressions for the [B] and [D] matrices will be presented later. Thus, including the
viscous damping, Eq. (5) becomes
(9)
Since the virtual displacement {d}is arbitrary, the governing equation of the system is
(10)
where,
= Mass matrix, (11)
= Stiffness matrix, (12)
and,
= Force vector. (13)
Thus, to summarise, the governing equations for free vibration problem is furnished below:
(14)
4.1. Governing Equations of Lamina:
4.1.1. Basic Constitutive Equations:
From the law of conservation of linear momentum, the equations of motion are given by:
ij,i
+ b
j
=
j
(15)
From the law of conservation of angular momentum, one may obtain
ij
ji
(16)
Constitutive relation of general linear anisotropic material is given by
ij
C
ijkl
kl
(17)
Combining above equations, and neglecting body force terms, equation of dynamic equilibrium
may be represented as
i
(C
ijkl
kl
)
j
= 0 (18)
Since
ij
is symmetrical, C
ijkl
must be symmetrical in i and j i.e.
C
ijkl
= C
jikl
(19)
Again for linear elastic problems, the strain tensor, given by
kl
= 0.5( u
k,l
+ u
l,k
), is also
symmetrical in l and k, therefore,
C
ijkl
= C
ijlk
(20)
Using strain energy density function, W, defined as the strain energy contained in a unit volume
of the structure undergoing deformation from an arbitrary datum, and given by
W=
C
ijkl
ij
kl
(21)
It can be obtained from mathematical identity
(22)
that, C
ijkl
= C
klij
. Finally it can be concluded that,
C
ijkl
= C
klij
= C
jikl
= C
ijlk
(23)
Now it can be shown that in general anisotropic element among the 81 elastic constant, 21 are
independent elastic constants.
Now the constitutive relationship can be written in pseudo-tonsorial form, with 21 material
constants, as
{
=
[
(24)
4.1.2. Elastic Stiffness Matrix:
Generally the constitutive relationship matrix c
ij
depend on the orientation of the co-ordinate
system. An isotropic material is characterized by infinite number of planes of material symmetry
through a point. An isotropic material is characterized by only two independent elastic constant,
c
11
, c
12
.
{
=
[
In case of an orthotropic material, which has three mutually perpendicular plane of symmetry,
number of independent elastic constant reduced to nine. For orthotropic material independent
coefficients are c
11
, c
12,
c
13,
c
22,
c
23,
c
33,
c
44,
c
55,
c
66.
{
=
[
(25)
For an orthotropic material following reciprocal law holds:
, (i, j=1, 2, 3)
The relation between the stiffness constant and the engineering constant for orthotropic material
is given by:
c
11
= E
1
, c
12
= E
1
= E
2
c
12
= E
1
= E
3
, c
22
= E
2
(26)
c
23
= E
2
= E
3
, c
33
= E
3
c
44
= G
23
, c
55
= G
31
, c
66
= G
12
,
= 1
12
21
23
32
31
13
2
21
32
13
Here, directions 1, 2 and 3 are directions of orthotropy
E
1
,E
2
,E
3
= Young moduli in 1, 2 and 3 directions, respectively
ij
= Poissons ratio of transverse strain in the j
th
direction to the axial strain in the
i
th
direction, when stressed in the i
th
direction.
= -
j
/
i
G
23
, G
13
,
G
12
= shear moduli in the 2-3, 1-3 and 1-2 planes, respectively.
A fiber-reinforced composite lamina is essentially an orthotropic material, since the presence of
fiber, say, along the direction 1, renders this direction more strength and stiffness compared to
directions normal to it. However, a lamina being essentially a thin plate, plane stress assumptions
apply here quite adequately. Hence, the elastic relations may be simplified as follows:
Q
11
=
, Q
22
=
, Q
12
=
12
Q
22
=
21
Q
11
, (27)
Q
44
= G
23
, Q
55
= G
31,
Q
66
= G
12
In general, though the transverse shear stresses
4
(or
23
) and
5
(or
31
), are not incorporated in
plane stress analysis, here these stresses are accounted so that the Mindlins plate theory may be
used instead of the conventional Kirchhoffs theory. In matrix form
{
=
[
(28)
Above matrix is decomposed in to two parts and the stress strain relations is rewritten in the
principal material direction 1, 2, and 3 as follows:
1
{
} = [
]
2
6
(29)
and {
} = [
] {
}
Fig. 1: Arbitrarily oriented Lamina
The stress
z
or
3
has been dropped in the Mindlins theory. The off axis stress strain relations of
the lamina, with respect to the x, y and z axes (Fig.1 ) are expressed as
x
y
2
1
x
Axis 3 coincides with axis z
{
} = [
]
y
xy
(30)
and {
} = [
] {
}
The above equation is based on the assumption that the fibres are oriented along the direction 1,
while the lamina lies on the 1-2 plane, directions 1 and 2 being mutually perpendicular. These
relations are termed as the on-axis relations. The off-axis relations are obtained by operating
suitable transformations on the on-axis relations. The off-axis relations are transformations
needed to get the stress-strain relations along the local axes defined on the plate (Fig. 2) :
Fig. 2. The orthotropic directions and local plate axes. The angle is termed as the fibre angle.
The elastic coefficients transformed from the orthotropic axes to the user-defined local co-
ordinates are written with primes to identify them properly. These transformation rules in explicit
form may be written as furnished below:
Where,
Q'
11
= m
4
Q
11
+ 2m
2
n
2
(Q
12
+2Q
66
) + n
4
Q
22
Q'
22
= n
4
Q
11
+ 2m
2
n
2
(Q
12
+2Q
66
) + m
4
Q
22
Q'
12
= m
2
n
2
(Q
11
+ Q
12
4Q
66
) + (m
4
+ n
4
) Q
12
Q'
16
= m
3
n (Q
11
Q
12
2Q
66
) mn
3
(Q
22
Q
12
2Q
66
) (31)
Q'
26
= mn
3
(Q
11
Q
12
2Q
66
) m
3
n (Q
22
Q
12
2Q
66
)
Q'
66
= m
2
n
2
(Q
11
+ Q
22
2Q
12
) + (m
2
n
2
) Q
66
Q'
44
= m
2
Q
44
+ n
2
Q
55
Q'
45
= mn (Q
55
Q
44
)
Q'
55
= m
2
Q
55
+ n
2
Q
44
4.2. Governing Equations of the Laminate :
General construction of laminated composite plate of thickness t consisting of unidirectional
lamina bonded together to act as an integral continuum, is pictorially explained in Fig. 3. The
bond are infinitesimally thin and are not shear deformable. Hence, the displacements are
continuous through the thickness of the laminate. In the present analysis the first order transverse
shear deformation is assumed. Thus a vertical plane cross section before deformation is assumed
to remain plane after deformation but it may not remain normal to the middle surface as it
happens with the Kirchhoffs plates.
The following assumption is made according to the Yang-Norris-Stavsky (YNS) theory [2]
which is a generalization of the Mindlin theory to accomodate composite laminates :
1. The material behavior is linear and elastic.
2. The thickness, t, of the laminate is small compared to the other two dimensions.
3. Displacements u, v, and W are small compared to the laminate thickness, h.
4. Normal to the mid-plane before deformation remains straight but not necessarily normal to the
mid-plane after deformation.
5. Stresses normal to the mid-plane are neglected.
4.2.1. Displacement Model :
The deformed geometry of the laminated plate is shown in Fig. 4 and Fig. 5. The displacement
model adopted for flat plates in the present analysis includes the in-plane displacements u
0
and v
0
at the mid-plane, an out-of-plane displacement w
0
, of the mid-plane and two rotations
x
and
y
as shown in Figs. 4 and 5. It may so happen that the vertical plane before bending is no longer
perpendicular to the middle surface after deformation. Again, the mid-plane may have in-plane
h/2
b/2
a/2
n
k
2
1
Oy
Ox
x, u
z, w
y, v Oz
Fig. 3. Laminated
composite plate with
positive displacements,
rotations.
translations too. The total rotation is the sum of the shear rotation and bending rotation, as
expressed in Eq. 21. The in-plane displacements and are assumed to vary linearly with depth,
proportional to the total rotation, plus the mid-plane displacement, whereas, the transverse
deflection is an invariant through the depth according to the assumptions of the YNS theory.
The in-plane displacements u and v of any point at a distance z from the mid-plane for a
Mindlin-composite plate are given by :
u(x, y, z, t) = u
0
+ z
y
(x, y, t)
v(x, y, z, t) = v
0
z
x
(x, y, t) (32)
w(x, y, z, t) = w
0
(x, y, t)
v
0
-z.x
F
y
-
x
-w, y
-w, y
z
y
Mid surface
Assumed
orientationof
CD
Mid surface normal
C
D
Fig. 5. A 2-dimensional
view of deformation of
the plate along a section
parallel to the y-z plane.
u
0
z.y
F
x
y
-w, x
-w, x
z
x
Mid surface
Assumed
Orientation of
AB
Mid surface normal
A
B
Fig. 4. A 2-dimensional
view of deformation of
the plate along a section
parallel to the x-z plane.
The shear rotation of the plate can be expressed as
x
=
y
+ w,
x
,
y
=
x
+ w,
y
(33)
Withholding the spatial and temporal co-ordinates, for a Mindlin plate the following
relations may be assumed for the displacement model :
u u
0
+ z
y
x
w
,y
-
y
v = v
0
z
x
and = (34)
y
-w,
x
+
x
w w
0
The displacements of the flat plate are fully described by five components, u, v, w,
x
and
y
,
where u, v and w are displacements along the x, y and z-directions and
x
and
y
are the linear
rotations of initially vertical planes on the x-z and y-z planes after distortion, at location (x,y) on
the mid-plane. The positive sign conventions for displacements and stress resultants are
illustrated in Fig. 3. The mid-plane displacements in the x-, y- and z-direction are u
0
, v
0
, w
0
(refer Figs. 4 and 5). With the displacements defined in Eq. (34), now the strains may be defined
in terms of displacements. This kinematic relationship will be taken up in the next section. The
definitions will be restricted within linear elastic zone however.
4.2.2. Strain-Displacement Relations
The linear in-plane strain of laminate at a distance z from the mid-surface are given by,
x
= u,
x
= u
0
,
x
+ z
y
,
x
=
0
x
+ z
x
y
= v,
y
= v
0
,
y
z
x
,
y
=
0
y
+ z
y
(35)
xy
= u,
y
+ v,
x
= u
0
,
y
+ v
0
,
x
+ z(
y
,
y
x
,
x
)
=
0
xy
+ z
xy
Since, the transverse shear deformation is assumed same across the thickness of the laminate are
given by,
xz
=
x
=
0
xz
,
yz
=
y
=
0
xz
(36)
Substituting equation (35), (36) in equation (30), the stress in any lamina k can be expressed in
terms of the laminate mid-surface strains, curvatures, shear rotations of the lamina.
{
} = [
} (i, j = 1, 2, 6)
{
} = [
} (i, j = 4, 5) (37)
And is a shear correction factor, taken as 5/6, to taken to account for the non uniform
distribution of the transverse shear strain across the thickness of the laminate.
4.2.3. Constitutive Relations for a Laminated Composite Plate :
The internal force and moment resultants of the laminate are obtained by integrating the lamina
stresses over the entire plate thickness. Thus stress terms are replaced by the stress-resultant
terms, while the conventional strain terms are replaced by the mid-plane strain terms. Thus,
assuming that the laminate comprises of n laminae, for the in-plane force,
[
] = [
=
[
dz
=
[]
dz
=
[]
dz
[
] = [
=
[
dz
=
[]
dz
=
z
[
] = [
=
[
dz (38)
=
[
dz
= [
] {
From equations (26), the internal force and moment resultants can be expressed as,
{F}= [D] {} (39)
Where, {F} = {N
x
, N
y
, N
xy
, M
x
, M
y
, M
xy
, Q
x
, Q
y
}
T
{}= {
x
,
y
,
xy
,
x
,
y
,
xy
,
x
,
y
}
T
= {
x
,
y
,
xy
,
x
,
y
,
xy
,
xz
,
yz
}
T
[D]=
[
The stiffness of the laminate are
(Aij, Bij, Dij) =
dz (i, j = 1, 2 and 6)
(Aij) =
dz (i, j = 4, 5)
4.2.4. Non-linear Strains :
Since the deflection w does not vary with z, the non-linear portion of the overall strains [52] in a
laminated plate can be expressed as
xnl
=
(u
2
,
x
+ v
2
,
y
+ w
2
,
x
)
xnl
=
(u
2
,
y
+ v
2
,
y
+ w
2
,
y
)
xynl
= (u,
x
u,
y
+ v,
x
v,
y
+ w,
x
w,
y
)
xznl
= (u,
x
u,
z
+ v,
x
v,
z
)
yznl
= (u,
y
u,
z
+ v,
y
v,
z
) (40)
From the equation (20)
xnl
=
[u
0
2
,
x
+ v
0
2
,
y
+ w
2
,
x
+ 2z(u
0
,
x
y
,
x
v
0
,
x
x
,
x
) + z
2
(
2
y
,
x
+
2
x
,
x
)]
ynl
=
[u
0
2
,
y
+ v
0
2
,
y
+ w
2
,
y
+ 2z(u
0
,
y
y
,
y
v
0
,
y
x
,
y
) + z
2
(
2
x
,
y
+
2
y
,
y
)]
xynl
= [u
0
,
x
u
0
,
y
+ v
0
,
x
v
0
,
y
+ w,
x
w,
y
+ z(u
0
,
y
y
,
x
+ u
0
,
x
y
,
y
) z(v
0
,
y
x
,
x
+ v
0
,
x
x
,
y
)
+ z
2
(
y
,
x
y
,
y
+
x
,
x
x
,
y
)]
xznl
= [u
0
,
x
y
v
0
,
x
x
+ z(
y
y
,
x
+
x
x
,
x
)]
yznl
= [u
0
,
y
y
v
0
,
y
x
+ z(
y
y
,
y
+
x
x
,
y
)] (41)
4.2.5. Principle of Total Potential Energy :
The potential energy of deformation of a laminated plate is given by
U =
{}
[]
{} (42)
The potential energy of inertia force and moment is expressed as
V
i
=
{}
{} (43)
where, {X} = {pu
0
2
n
, pv
0
2
n
, pw
2
n
, I
x
2
n
, I
y
2
n
,}
T
in which,
p =
, I =
The total potential energy in respect of free vibration of laminated plates in is
= U + V
i
(44)
According to the principle of total potential Energy the first variation of in equation (44) is
stationary for the equilibrium of laminated plate. Thus by equating to zero in equations (44),
the respective equilibrium conditions are obtained.
4.3 Equations of Motion
For any three-dimensional object the equations of motion is given by
(45)
where,
ij
stand for the stress components, B
i
for the body force components, is the
mass
density and
are the acceleration components of the structure. In the absence of body force,
eq.
(45) can be expanded as
(46)
Substituting the expanded form of u, v and w from Eq. (2.6.1) for plate structures
(47a)
(47b)
(47c)
From integration of Eq (47a) over depth z = h/2 it is obtained that
(48)
The third term in the left-hand-side is taken to zero since the transverse shear at top and bottom
of the plate structures are identically zero. Similar treatment to (47b) produces
(49)
Finally, from (47c), upon integration over depth the third equation of motion is found :
(50)
Two more equations of motion can be obtained by multiplying both sides of Eqs. (47a) and (47b)
by depth co-ordinate z and integrating over the thickness. Thus,
(51)
Likewise, the last equation of motion is given by
(52)
In matrix form the equation of motions for the Mindlin plate may be written as follows :
(53)
or,
(54)
where {F} is the force vector, [] is the inertia matrix, and {A} is the acceleration vector.
4.4. Finite Element Formulation :
The finite element formulation is based on the governing equation derived in section 4. The
element stiffness, geometric stiffness and mass matrices are derived using the Principle of Total
Potential Energy. A nine nodded Lagrangian isoparametric element have been used. Both the
geometry and displacement field are expressed in terms of same shape functions. The parent
element in local natural co-ordinate system can be mapped to an arbitrary shape in the Cartesian
co-ordinate system. In Section 4 the expressions for the governing equations are derived with the
assumption that the entire region of interest is a continuum. In finite element ideology, however,
the continuum is visualised as an ensemble of finite number of user-defined elements, with finite
number of nodes at their vertices, and the elements are connected to their neighbouring elements
via the nodes only and not the interfaces. However, in general cases it is assumed that the
elements boundaries do not separate or overlap, that is, the continuity is maintained throughout
the continuum and inter-element interfaces. The intra-element properties are obtained from the
nodal values, through interpolation functions, as described in Eq. (6). However, now the
interpolation functions involve contributions only from the element nodes and not from all the
structural nodes. This produces the same set of final outputs as in Eqs. (10), (11), (12), wherein
the element mass and stiffness matrices are obtained. However, the integration over the depth of
the plate are incorporated in the constitutive relations in an earlier stage (Section 4.2.3.), and
hence the integrations are carried out over the area of the elements only with the help of Gauss
Legendre quadrature. Thus the element matrices are given as below
= Mass matrix (55)
= Stiffness matrix (56)
and,
= Force vector (57)
Here and are the element natural co-ordinates and |J| is the determinant of the
Jacobian
matrix [J] =
(58)
nel being the number of nodes per element. The analyses are done in single dimensional storage
arrays using Subspace iteration for eigen problems.
4.4.1. Isoparametric Element :
The isoparametric means same parameters and is applied here because same interpolation
functions are used to interpolate the magnitude of co-ordinates as well as the degree of freedom.
If the interpolation functions for the degrees of freedom are of higher order than those used for
co-ordinate interpolations, the element is called subparametric, while the reverse is the case for
superparametric elements. By the use of isoparametric elements it is easier to simulate
complicated geometries, while simplifying the computations simultaneously. A flat Mindlin-
plate element, in general, has five displacement degrees of freedom at each node as shown in Eq.
(30). Nine noded Lagrangian element [Fig 6.] with five degree of freedom at each node, i.e., u
0
,
v
0
, w,
x
,
y
is considered for finite element formulation.
Fig. 6. Nine noded Lagrangian element
The co-ordinates and the elastic parameters inside an element can be interpolated using the shape
functions and the nodal values as follows:
(59)
Here, NEL stands for nodes per element, whereas, u
i
stands for the five intra-element
displacement components u
o
, v
o
, w
o
,
x
, and
y
at node i
while d
i
are the corresponding nodal
displacements at node i, both considered at the middle surface of the plate.
The shape functions N
j
in equations (59) are defined as
N
j
= (
2
+
j
)(
2
+
j
)/4; j = 1,2,3,4
N
j
=
j
2
(
2
j
) (1
2
)/2 +
j
2
(
2
j
)(1
2
)/2; j = 5,6,7,8
N
j
= (1
2
) (1
2
); j = 9 (60)
Where and are the local natural co-ordinates of the element and
j
and
j
are the value of them
at node j.
The strains at the mid-plane may be similarly written by taking the derivatives of the shape
functions with respect to the spatial co-ordinates as shown below :
(61)
Or,
(62)
Since the shape functions, the elastic matrix, [D], and the inertia matrix, [], are already known,
as cited in Fig. (6) and Eqs. (39) and (49), the element stiffness and mass arrays can be easily
computed in local axes using Eqs. (55) and (56). These element arrays are next transformed to fit
the global axes before they are properly assembled. In the next section the transformation matrix
is formed and the transformation to be applied over the element matrices are summarily
discussed for completeness.
The derivatives of the shape functions N
j
with respect to x and y are expressed in terms of their
derivatives with respect to and by the following relationship:
N
j,x
= [J]
-1
N
j,
N
j,y
N
j,
Where, [J] = [
] = Jacobian matrix
The Principle of Total Potential Energy described in sec. 4.2.5 is applied for the element to
derive the stiffness and mass matrices.
4.4.2. Element Stiffness Matrix:
The potential energy of deformation for the element, given by equation (29), is
U =
{}
[]
{} (64)
if {} = [B]{
e
} = [[B
1
] [B
2
] [B
9
]] {
e
}
(65)
where {}= {
x
y
xy
x
y
xy
xz
yz
}
T
{
e
} = {u
01
, v
01
, w
1
,
x1
,
y1
u
09
, v
09
, w
9
,
x9
,
y9
}
T
[B
i
] =
[
(i = 1 to 9)
then U =
{}
[]
[][]
{}
=
{}
[
{
e
}
in which [K
e
] = []
[][]
= element stiffness matrix. (66)
Since dx dy = |J| d d , where |J| is the determinant of the Jacobian matrix, the element stiffness
matrix can be expressed in local natural coordinates of the element. From equation (66),
[K
e
] = []
[][]
(67)
4.4.3. Element Mass Matrix :
The potential energy of inertia forces for the element is obtained from equation (31)
V
i
=
{}
{} (68)
where, {X} =
n
2
[P] {u
0
v
0
w
x
y
}
T
in which, [P] =
[
Therefore,
V
ie
=
[]
[] [] {
] {
}
Where [
] []
[] []
= element mass matrix (69)
where, [N] = [ [N
1
] [N
2
] ..[N
8
] [N
9
] ]
where [N
i
] =
[
( i = 1 to 9)
4.4.4. Finite Element Transformation :
The positive directions of the linear displacements for a plate element are shown in Fig. 7a. The
rotations are shown in Fig. 7b. Also Fig. 3 may be referred to. To retain parity with the sense of
rotations in most common texts the rotation is found to contradict with the right hand screw
direction. Accordingly, a transformation is planned.
Fig. 7(a). Transformation of translations Fig. 7(b). Transformation of rotations
from local (x) to global (x ) axis. from local (x) to global (x ) axes.
From Figs. 7, the relation between the local displacements u, v, w,
x
,
y
,
z
and the global
displacements u, v, w,
x
,
y
,
z
are given by the following matrix expression:
or,
(70)
It may be noted that the transformation matrix [T] is orthogonal, i.e., [T]
T
=[T]
-1
.
In local axis, let the equation of motion be
(71)
In the same way as in Eq. (70), the displacement, velocity and acceleration terms can be
transformed from global (gl) to local (loc) axes as follows
(72)
Using these relations, Eq. (71) can be written as
Pre-multiplying both sides by [T]
T
( [T]
-1
), produces the equation in global co-ordinates :
or,
(73)
where,
(74)
(75)
(76)
The stiffness and mass matrices of an element is expressed accordingly global co-ordinates from
local co-ordinates using transformation matrix as follows:
[K
gl
] = [T]
T
[K
loc
]
[T]
[M
gl
] = [T]
T
[M
loc
]
[T]
Before applying the transformation, the 4545 stiffness and mass matrices are expanded to
5454 by inserting nine
z
drilling degree of freedom at each node of a finite element.
The various element matrices [K
gl
] and [M
gl
] are assembled to obtain their respective global
matrices [K] and [M] by incorporating boundary conditions during assembly stage.
4.4.5. Solution Process:
The minimization of in the equation (44) leads the following equilibrium conditions for the
free vibration of the laminated plates.
( [K]
n
2
[M] ) {} = 0
From which the natural frequencies are determined.
Potrebbero piacerti anche
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeDa EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeValutazione: 4 su 5 stelle4/5 (5794)
- Column 9Documento1 paginaColumn 9Ankur GhoshNessuna valutazione finora
- Shoe Dog: A Memoir by the Creator of NikeDa EverandShoe Dog: A Memoir by the Creator of NikeValutazione: 4.5 su 5 stelle4.5/5 (537)
- Ch17solution ManualDocumento22 pagineCh17solution ManualStoneCold Alex Mochan100% (2)
- Unfiled NotesDocumento2 pagineUnfiled NotesAnkur GhoshNessuna valutazione finora
- The Yellow House: A Memoir (2019 National Book Award Winner)Da EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Valutazione: 4 su 5 stelle4/5 (98)
- Pet-Cut Off Merit 2009 10Documento16 paginePet-Cut Off Merit 2009 10Ankur GhoshNessuna valutazione finora
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceDa EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceValutazione: 4 su 5 stelle4/5 (895)
- When I Was Ten Years OldDocumento1 paginaWhen I Was Ten Years OldAnkur GhoshNessuna valutazione finora
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersDa EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersValutazione: 4.5 su 5 stelle4.5/5 (344)
- SFRC 1Documento1 paginaSFRC 1Ankur Ghosh100% (1)
- The Little Book of Hygge: Danish Secrets to Happy LivingDa EverandThe Little Book of Hygge: Danish Secrets to Happy LivingValutazione: 3.5 su 5 stelle3.5/5 (399)
- Gen. Ref. Book PDFDocumento9 pagineGen. Ref. Book PDFsaleemm_2Nessuna valutazione finora
- Grit: The Power of Passion and PerseveranceDa EverandGrit: The Power of Passion and PerseveranceValutazione: 4 su 5 stelle4/5 (588)
- Column 15Documento1 paginaColumn 15Ankur GhoshNessuna valutazione finora
- The Emperor of All Maladies: A Biography of CancerDa EverandThe Emperor of All Maladies: A Biography of CancerValutazione: 4.5 su 5 stelle4.5/5 (271)
- Column 16Documento5 pagineColumn 16Ankur GhoshNessuna valutazione finora
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaDa EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaValutazione: 4.5 su 5 stelle4.5/5 (266)
- Seismic Base IsolationDocumento24 pagineSeismic Base IsolationAnkur GhoshNessuna valutazione finora
- Never Split the Difference: Negotiating As If Your Life Depended On ItDa EverandNever Split the Difference: Negotiating As If Your Life Depended On ItValutazione: 4.5 su 5 stelle4.5/5 (838)
- Topic15 7 SeismicIsolationNotesDocumento87 pagineTopic15 7 SeismicIsolationNotesFlorin MacinicNessuna valutazione finora
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryDa EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryValutazione: 3.5 su 5 stelle3.5/5 (231)
- Buckling of Laminated Plates With CutoutsDocumento2 pagineBuckling of Laminated Plates With CutoutsAnkur GhoshNessuna valutazione finora
- Shear Test of SFRCDocumento4 pagineShear Test of SFRCAnkur GhoshNessuna valutazione finora
- On Fire: The (Burning) Case for a Green New DealDa EverandOn Fire: The (Burning) Case for a Green New DealValutazione: 4 su 5 stelle4/5 (73)
- PDFDocumento37 paginePDFAlex Gomez LlallahuiNessuna valutazione finora
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureDa EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureValutazione: 4.5 su 5 stelle4.5/5 (474)
- 101 Keyboard ShortcutsDocumento6 pagine101 Keyboard Shortcutslittle cute gurlz100% (4)
- Team of Rivals: The Political Genius of Abraham LincolnDa EverandTeam of Rivals: The Political Genius of Abraham LincolnValutazione: 4.5 su 5 stelle4.5/5 (234)
- Eticket: Kolkata Durgapur Saturday, June 3, 2017Documento2 pagineEticket: Kolkata Durgapur Saturday, June 3, 2017Ankur GhoshNessuna valutazione finora
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyDa EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyValutazione: 3.5 su 5 stelle3.5/5 (2259)
- ch-4 MS ShettyDocumento5 paginech-4 MS ShettyShshank MattooNessuna valutazione finora
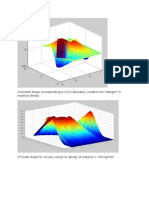
- 2nd Mode Shape Corresponding To CCCC Boundary Condition For 700Kg/m 3 Material DensityDocumento2 pagine2nd Mode Shape Corresponding To CCCC Boundary Condition For 700Kg/m 3 Material DensityAnkur GhoshNessuna valutazione finora
- Indian Oil Corporation Limited: Application Form (Personal & Confidential)Documento1 paginaIndian Oil Corporation Limited: Application Form (Personal & Confidential)Ankur GhoshNessuna valutazione finora
- ff381020 - Activation IDDocumento1 paginaff381020 - Activation IDAnkur GhoshNessuna valutazione finora
- Thesis II FinalDocumento6 pagineThesis II FinalAnkur GhoshNessuna valutazione finora
- The Unwinding: An Inner History of the New AmericaDa EverandThe Unwinding: An Inner History of the New AmericaValutazione: 4 su 5 stelle4/5 (45)
- In 1964 SchlackDocumento1 paginaIn 1964 SchlackAnkur GhoshNessuna valutazione finora
- GRE PasswordDocumento1 paginaGRE PasswordAnkur GhoshNessuna valutazione finora
- SLS and ULS CombinationDocumento1 paginaSLS and ULS CombinationAnkur GhoshNessuna valutazione finora
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreDa EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreValutazione: 4 su 5 stelle4/5 (1090)
- In 1964 SchlackDocumento1 paginaIn 1964 SchlackAnkur GhoshNessuna valutazione finora
- AcknowledgementDocumento2 pagineAcknowledgementAnkur GhoshNessuna valutazione finora
- Certificate of ApprovalDocumento2 pagineCertificate of ApprovalAnkur GhoshNessuna valutazione finora
- ConcreteDocumento5 pagineConcreteAnkur GhoshNessuna valutazione finora
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)Da EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Valutazione: 4.5 su 5 stelle4.5/5 (120)
- HiDocumento2 pagineHiAnkur GhoshNessuna valutazione finora
- Soil Engineering & Geotechnics: Analysis of Potential ProblemsDocumento1 paginaSoil Engineering & Geotechnics: Analysis of Potential ProblemsdzingoNessuna valutazione finora
- 2 Marks With AnswersDocumento16 pagine2 Marks With AnswersKarthik SoundarrajanNessuna valutazione finora
- Tugas Bahasa Inggris - Main IdeaDocumento2 pagineTugas Bahasa Inggris - Main IdeaMAWAR08Nessuna valutazione finora
- 2016 HSC Engineering StudiesDocumento40 pagine2016 HSC Engineering StudiesR MathewNessuna valutazione finora
- 3-Torsion of Circular Shafts PDFDocumento28 pagine3-Torsion of Circular Shafts PDFMohamad Zaid75% (4)
- Stability of Buildings Part 4 Moment FramesDocumento57 pagineStability of Buildings Part 4 Moment Framesalextse100% (4)
- Buckling Behaviors of Section Aluminum Alloy Columns Under Axial Compression PDFDocumento11 pagineBuckling Behaviors of Section Aluminum Alloy Columns Under Axial Compression PDFdjordjeueNessuna valutazione finora
- ENSC 24a - Strength of MaterialsDocumento9 pagineENSC 24a - Strength of MaterialsalexontingNessuna valutazione finora
- DME-Tutorial-Module 2-Part A - 22 Sep 2020 - To StudentsDocumento17 pagineDME-Tutorial-Module 2-Part A - 22 Sep 2020 - To StudentsMathew JohnNessuna valutazione finora
- Fatigue PDFDocumento67 pagineFatigue PDFsabaris ksNessuna valutazione finora
- Her Body and Other Parties: StoriesDa EverandHer Body and Other Parties: StoriesValutazione: 4 su 5 stelle4/5 (821)
- BOX Section Calculations IRC18, IRC 112Documento55 pagineBOX Section Calculations IRC18, IRC 112pravinNessuna valutazione finora
- The American University in Cairo: ENGR 2112/229 Experiment 2: Tension Test Part 2Documento29 pagineThe American University in Cairo: ENGR 2112/229 Experiment 2: Tension Test Part 2Cherif ChokeirNessuna valutazione finora
- Tabel Profil Baja - 1 - WFDocumento8 pagineTabel Profil Baja - 1 - WFDomasandi SuharnoNessuna valutazione finora
- 4 - Analysis of Wind Turbine Blades Aeroelastic Performance Under Yaw ConditionsDocumento12 pagine4 - Analysis of Wind Turbine Blades Aeroelastic Performance Under Yaw ConditionsMayra ZezattiNessuna valutazione finora
- Stress Strain RelationsDocumento22 pagineStress Strain Relationsmustafa1011Nessuna valutazione finora
- Applications of The Theory of Plasticity ToDocumento170 pagineApplications of The Theory of Plasticity Tomark_zarcoNessuna valutazione finora
- Appraising Stone Column Settlement Prediction Methods Using Finite Element AnalysesDocumento20 pagineAppraising Stone Column Settlement Prediction Methods Using Finite Element AnalysesZOUABINessuna valutazione finora
- 1714 Deep Beams Concept Applications Assumptions A Differences Between Deep A Simple BeamsDocumento3 pagine1714 Deep Beams Concept Applications Assumptions A Differences Between Deep A Simple BeamsNikhil Babaria0% (2)
- Experimental and Numerical Study of The Flexural Behaviour of Ultra-HighDocumento14 pagineExperimental and Numerical Study of The Flexural Behaviour of Ultra-HighjayanthNessuna valutazione finora
- Elastic Constants KetulDocumento21 pagineElastic Constants KetulRambabu Vurimi67% (3)
- Undrained Behaviour (And Modelling) : Computational Geotechnics CourseDocumento46 pagineUndrained Behaviour (And Modelling) : Computational Geotechnics Courselphuong_20Nessuna valutazione finora
- Steel Deck DesignDocumento25 pagineSteel Deck DesignJanaka KarunarathnaNessuna valutazione finora
- 3180 5656 1 SM PDFDocumento6 pagine3180 5656 1 SM PDFkarhiklekkala7Nessuna valutazione finora
- Strength of Materials W - B: ORK OOKDocumento76 pagineStrength of Materials W - B: ORK OOKAlex DupriusNessuna valutazione finora
- MEng6302 Lecture 8 Bending of Prismatic Bar ASM 2021Documento38 pagineMEng6302 Lecture 8 Bending of Prismatic Bar ASM 2021KKDhNessuna valutazione finora
- Analysis of Continuous Fiber Composites - I: Reinforced Plastics (Composite)Documento3 pagineAnalysis of Continuous Fiber Composites - I: Reinforced Plastics (Composite)أحمد صدقيNessuna valutazione finora
- Mechanics of MaterialDocumento3 pagineMechanics of MaterialChhaya Sharma100% (1)
- Crack Propagation in Aluminum Sheets PDFDocumento248 pagineCrack Propagation in Aluminum Sheets PDFvidal3213Nessuna valutazione finora
- Nested Conditional and Iterative StatementsDocumento11 pagineNested Conditional and Iterative StatementsHarriette MojicaNessuna valutazione finora
- Custom Impression Trays: Part I-Mechanical Properties: IjniDocumento4 pagineCustom Impression Trays: Part I-Mechanical Properties: IjniaabdoNessuna valutazione finora
- The End of Craving: Recovering the Lost Wisdom of Eating WellDa EverandThe End of Craving: Recovering the Lost Wisdom of Eating WellValutazione: 4.5 su 5 stelle4.5/5 (80)
- Sully: The Untold Story Behind the Miracle on the HudsonDa EverandSully: The Untold Story Behind the Miracle on the HudsonValutazione: 4 su 5 stelle4/5 (103)
- Highest Duty: My Search for What Really MattersDa EverandHighest Duty: My Search for What Really MattersNessuna valutazione finora
- Hero Found: The Greatest POW Escape of the Vietnam WarDa EverandHero Found: The Greatest POW Escape of the Vietnam WarValutazione: 4 su 5 stelle4/5 (19)
- The Beekeeper's Lament: How One Man and Half a Billion Honey Bees Help Feed AmericaDa EverandThe Beekeeper's Lament: How One Man and Half a Billion Honey Bees Help Feed AmericaNessuna valutazione finora
- ChatGPT Money Machine 2024 - The Ultimate Chatbot Cheat Sheet to Go From Clueless Noob to Prompt Prodigy Fast! Complete AI Beginner’s Course to Catch the GPT Gold Rush Before It Leaves You BehindDa EverandChatGPT Money Machine 2024 - The Ultimate Chatbot Cheat Sheet to Go From Clueless Noob to Prompt Prodigy Fast! Complete AI Beginner’s Course to Catch the GPT Gold Rush Before It Leaves You BehindNessuna valutazione finora
- The Intel Trinity: How Robert Noyce, Gordon Moore, and Andy Grove Built the World's Most Important CompanyDa EverandThe Intel Trinity: How Robert Noyce, Gordon Moore, and Andy Grove Built the World's Most Important CompanyNessuna valutazione finora
- Faster: How a Jewish Driver, an American Heiress, and a Legendary Car Beat Hitler's BestDa EverandFaster: How a Jewish Driver, an American Heiress, and a Legendary Car Beat Hitler's BestValutazione: 4 su 5 stelle4/5 (28)
- The Fabric of Civilization: How Textiles Made the WorldDa EverandThe Fabric of Civilization: How Textiles Made the WorldValutazione: 4.5 su 5 stelle4.5/5 (57)