Documenti di Didattica
Documenti di Professioni
Documenti di Cultura
Espacios Vectoriales
Caricato da
Joel HuillcaDescrizione originale:
Copyright
Formati disponibili
Condividi questo documento
Condividi o incorpora il documento
Hai trovato utile questo documento?
Questo contenuto è inappropriato?
Segnala questo documentoCopyright:
Formati disponibili
Espacios Vectoriales
Caricato da
Joel HuillcaCopyright:
Formati disponibili
ESPACIOS VECTORIALES
En las siguientes notas, usaremos el smbolo K para denotar o bien al conjunto de los n umeros reales
R o bien al conjunto de los n umeros complejos C. Los elementos de K seran llamados escalares.
1 Espacios Vectoriales
Un espacio vectorial (sobre K) consiste de:
1. Un conjunto no vaco E. Los elementos de este conjunto son conocidos como vectores.
2. Una funcion + : EE E. Esta funcion es conocida como adicion y, para cada par de vectores
u, v E, el vector +(u, v) es denotado por u +v.
3. Una funcion : K E E. Esta funcion es conocida como producto por un escalar. Para
cada escalar K y cada vector u E, el vector (, u) es denotado por u o por u.
Ademas, para cualesquiera escalares , K y cualesquiera vectores u, v, w E, se deben satisfacer
las siguientes propiedades:
Conmutatividad: u +v = v +u.
Asociatividad: (u +v) +w = u + (v +w) y ()u = (u).
Vector nulo: Existe un unico vector de E, que es denotado por 0 y es llamado vector nulo,
tal que x + 0 = 0 +x = x para todo vector x de E.
Inverso aditivo: Para cada vector x de E, existe un unico vector de E, que es denotado por
x y es conocido como el inverso aditivo de x tal que x + (x) = (x) +x = 0.
Distributividad: ( +)u = u +u y (u +v) = u +v.
Multiplicacion por 1: 1 u = u.
Aunque el espacio vectorial es formado por la tripla (E, +, ), en muchas ocasiones la adicion y el
producto por escalar estaran sobreentendidas o denidas de manera natural y entonces es com un
referirnos a E como espacio vectorial.
Observaciones: A partir de las propiedades anteriores, podemos deducir las siguientes.
Si los vectores x, u, v E son tales que x +u = x +v, entonces u = v.
En efecto,
u = 0 +u = ((x) +x) +u = (x) + (x +u) = (x) + (x +v) = ((x) +x) +v = 0 +v = v .
1
Para todo vector u E se cumple que 0 u = 0.
En efecto,
0 u + 0 = 0 u = (0 + 0)u = 0 u + 0 u,
y entonces 0 = 0 u.
Para todo escalar K se cumple que 0 = 0.
Tenemos que
0 + 0 = 0 = (0 + 0) = 0 + 0 ,
y entonces 0 = 0.
Si K y u E son tales que u ,= 0, entonces ,= 0 y u ,= 0.
Si u E, entonces (1) u = u.
Basta ver que
0 = 0 u = (1 + (1)) u = 1 u + (1) u = u + (1) u.
Ejemplos:
1. El espacio vectorial K
n
. Si n es un entero positivo, los elementos de K
n
son las listas ordenadas
de escalares u = (
1
,
2
, . . . ,
n
), es decir,
K
n
= u = (
1
,
2
, . . . ,
n
) :
1
,
2
, . . . ,
n
K .
Si u = (
1
,
2
, . . . ,
n
), v = (
1
,
2
, . . . ,
n
) son elementos de K
n
y es un escalar, la adicion y
el producto por escalar son denidos de la siguiente manera.
u +v := (
1
+
1
,
2
+
2
, . . . ,
n
+
n
) ,
u := (
1
,
2
, . . .
n
) .
El vector nulo es el vector 0 = (0, 0, . . . , 0) K
n
.
El inverso aditivo del vector u = (
1
,
2
, . . . ,
n
) es el vector u = (
1
,
2
, . . . ,
n
).
Si tomamos K = R, obtendremos el espacio euclidiano ndimensional R
n
.
Si tomamos K = C, obtendremos el espacio complejo ndimensional C
n
.
2. El espacio vectorial real /(mn). Si m, n son enteros positivos, una matriz real A de orden
mn es una lista de n umeros reales con ndices duplos a
ij
, con i = 1, 2, . . . , m y j = 1, 2, . . . , n.
Es com un representar a la matriz A como un arreglo rectangular con m las y n columnas de
n umeros reales, es decir,
A = (a
ij
) =
a
11
a
12
a
1n
a
21
a
22
a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
m1
a
m2
a
mn
.
2
El conjunto de todas las matrices reales de orden mn es denotado por /(mn).
Si A = (a
ij
), B = (b
ij
) son matrices reales de orden m n y es un n umero real, la adicion y
el producto por escalar son denidos de la siguiente manera.
A+B := (c
ij
), con c
ij
= a
ij
+b
ij
para i = 1, 2, . . . , m; j = 1, 2, . . . , n,
A := (p
ij
), con p
ij
= a
ij
para i = 1, 2, . . . , m; j = 1, 2, . . . , n.
La matriz nula es aquella con todas sus componentess iguales a 0 y el inverso aditivo de la matriz
A = (a
ij
) es la matriz A = (a
ij
).
3. El espacio vextorial real T(X, R). Si X es un conjunto no vaco, T(X, R) es denido como
el conjunto de todas las funciones f : X R.
Si f, g son dos funciones en T(X, R) y es un n umero real, la adicion y el producto por escalar
son denidos por
(f +g)(x) = f(x) +g(x) , para todo x X ,
( f)(x) = f(x) , para todo x X .
2 Subespacios Vectoriales
Sean E un espacio vectorial y S un subconjunto no vaco de E. Se dice que S es un subespacio
vectorial de E si satisface las dos siguientes propiedades:
1. Si u, v son vectores de S, entonces la suma u +v es un vector de S.
2. Si u es un vector de S y es un escalar, entonces u es un vector de S.
Observaciones:
Si S es un subespacio vectorial de E, entonces existe u S y
0 = 0 u S ,
es decir, el vector nulo siempre es un elemento del subespacio vectorial S.
Sea S un subespacio vectorial de E y considere las funciones +
S
: S S S,
S
: R S S
denidas por
+
S
(u, v) = +(u, v) = u +v ,
S
(, u) = (, u) = u,
entonces (S, +
S
,
S
) es un espacio vectorial.
Si S es un subespacio vectorial de E;
1
,
2
, . . . ,
m
R y v
1
, v
2
, . . . , v
m
S, entonces
v =
1
v
1
+
2
v
2
+ +
m
v
m
S .
Un vector v generado de esta manera es conocido como una combinacion lineal de los vec-
tores v
1
, v
2
, . . . , v
m
.
3
El subconjunto unitario 0 de E es un subespacio vectorial de E conocido como el subespacio
trivial.
El conjunto E es un subespacio vectorial de E conocido como el subespacio total.
Ejemplos:
1. Si E es un espacio vectorial y v es un vector no nulo de E, el conjunto S = v : R de
todos los m ultiplos de v es un subespacio vectorial de E. Este conjunto es conocido como la
recta que pasa por el origen y contiene a v.
2. Los subespacios vectoriales del espacio euclidiano R son:
El subespacio trivial 0.
El subespacio total R.
3. Los subespacios vectoriales del espacio euclidiano R
2
son:
El subespacio trivial 0.
Las rectas que pasan por el origen.
El subespacio total R
2
.
4. El conjunto C([a, b], R) formado por las funciones reales continuas denidas sobre el intervalo
[a,b], es decir,
C([a, b], R) = f : [a, b] R : f es continua ,
es un subespacio vectorial del espacio vectorial T([a, b], R).
Ejercicio. Sean E un espacio vectorial y S
: una familia no vaca de subespacios vectoriales
de E. Pruebe que la interseccion de estos subespacios,
S =
,
tambien es un subespacio vectorial de E.
Sea X un subconjunto no vaco de un espacio vectorial E.
Sea T la familia de todos los subespacios vectoriales de E que contienen a X. Esta familia es no
vaca (ya que E T) y entonces (por el ejercicio anterior) podemos deducir que la interseccion
de estos subespacios vectoriales,
S
X
=
SF
S ,
es tambien un subespacio vectorial de E. Este subespacio es conocido como el menor subes-
pacio vectorial de E que contiene a X y satisface la siguiente propiedad:
Si S es un subespacio vectorial de E que contiene a X, entonces S contiene a S
X
.
4
El conjunto span(X) formado por todos los vectores que son combinaciones lineales de algunos
vectores de X, es decir,
span(X) = v =
1
v
1
+
2
v
2
+ +
k
v
k
: k Z
+
;
1
,
2
, . . . ,
k
R; v
1
, v
2
, . . . , v
k
X ,
es un subespacio vectorial de E llamado subespacio vectorial de E generado por X.
Se dice que X genera E cuando span(X) = E.
Teorema 1. S
X
= span(X).
Si S
1
y S
2
son subespacios vectoriales de E, entonces el conjunto
S
1
+S
2
= u +v : u S
1
; v S
2
tambien es un subespacio vectorial de E conocido como la suma de S
1
y S
2
. Cuando S
1
S
2
= 0,
el subespacio vectorial S
1
+S
2
es denotado por S
1
S
2
y es conocido como la suma directa de los
subespacios S
1
y S
2
.
Ejercicio. Si S
1
y S
2
son subespacios vectoriales de E, entonces S
1
+ S
2
coincide con el subespacio
vectorial de E generado por S
1
S
2
.
Ejercicio. Sean S
1
, S
2
, S subespacios vectoriales de E com S
1
, S
2
S. Las siguientes armaciones
son equivalentes:
(i) S = S
1
S
2
.
(ii) Todo vector v S puede ser escrito de manera unica como una suma v = v
1
+ v
2
, con v
1
S
1
y v
2
S
2
.
Sea E un espacio vectorial. Si x, y son dos vectores distintos de E, el segmento que une los puntos
x e y es denido como el conjunto
xy := (1 t)x +ty : t [0, 1] ,
y la recta que une los puntos x e y es denida por
xy := (1 t)x +ty : t R .
Un subconjunto X de E es llamado convexo cuando para todo par de puntos distintos x, y de X se
cumple que xy X.
Un subconjunto X de E es llamado variedad afn cuando para todo par de puntos distintos x, y de
X se cumple que
xy X.
Ejercicios. Sean E un espacio vectorial, y X un subconjunto no vaco de E.
1. Pruebe que la interseccion de una familia de conjuntos convexos de E es tambien un conjunto
convexo de E. En particular, si ( es la familia de conjuntos convexos de E que contienen a X,
entonces la interseccion,
C(X) =
CC
C ,
es el menor conjunto convexo de E que contiene a X y satisface la siguiente propiedad:
5
Si C es un conjunto convexo de E con C X, entonces C C(X)
C(X) es conocida como la envolvente convexa o la envoltura convexa de X.
2. Pruebe que la envolvente convexa C(X) de X esta formada por todas las combinaciones convexas
de los puntos de X. Es decir,
C(X) = t
1
v
1
+ +t
k
v
k
: k Z
+
; v
1
, . . . , v
k
X; t
1
, . . . , t
k
0; t
1
+ +t
k
= 1 .
3. Pruebe que la interseccion de una familia de variedades anes de E es una variedad afn de E.
4. Sea V una variedad afn no vaca de E. Pruebe que existe un unico subespacio vectorial S de E
tal que, para todo x V , se cumple
V = x +S = x +v : v S .
3 Bases
Sean E un espacio vectorial y X un subconjunto no vaco de E.
Se dice que X es linealmente dependiente (L.D.) si hay algunos vectores (al menos uno) distintos
v
1
, v
2
, . . . , v
m
de X y algunos escalares
1
,
2
, . . . ,
m
, no todos nulos, tales que
1
v
1
+
2
v
2
+ +
m
v
m
= 0 .
Cuando X no es linealmente dependiente, se dice que X es linealmente independiente (L.I.) . En
este caso, se dice tambien que los vectores que conforman X son linealmente independientes.
Observaciones:
De manera practica, cuando se quiere demostrar que un conjunto de vectores v
1
, v
2
, . . . , v
m
es
L.I. se asume que existen escalares
1
,
2
, . . . ,
m
tales que
1
v
1
+
2
v
2
+ +
m
v
m
,
y luego se debe demostrar que
1
=
2
= =
m
= 0.
Si v
1
, v
2
, . . . , v
m
son vectores L.I. y
1
,
2
, . . . ,
m
,
1
,
2
, . . . ,
m
son escalares tales que
1
v
1
+
2
v
2
+ +
m
v
m
=
1
v
1
+
2
v
2
+ +
m
v
m
,
entonces
i
=
i
, para i = 1, 2, . . . , m.
Si en la sucesion de vectores v
1
, v
2
, . . . , v
m
, ninguno (a partir del segundo) puede ser expresado
como combinacion lineal de los anteriores, entonces estos vectores son L.I.
Sea E un espacio vectorial. Una base de E es un subconjunto B de E que es L.I. y que genera E.
Proposicion 2. Sea B un subconjunto no vaco de E. B es una base de E si y s olo si, todo vector de
E puede ser expresado de manera unica como combinacion lineal de algunos vectores de B.
6
Si B = v
1
, v
2
, . . . , v
m
es una base de E y v es un vector de E entonces (por la proposicion anterior)
existen unicos escalares
1
,
2
, . . . ,
m
tales que
v =
1
v
1
+
2
v
2
+ +
m
v
m
.
Los escalares
1
,
2
, . . . ,
m
son conocidos como las coordenadas de v en la base B.
Lema 1. Si v
1
, v
2
, . . . , v
m
es un conjunto de generadores de E, y u
1
, u
2
, . . . , u
k
es un conjunto de
vectores linealmente independientes de E, entonces m k.
Como consecuencia de este lema podemos ahora obtener facilmente el resultado central de esta seccion.
Teorema 3. Si el espacio vectorial E admite una base nita B, entonces cualquier otra base de E
posee la misma cantidad de elementos que B.
As, si E posee una base nita, se dice que E es de dimension nita y se dene la dimension de E
como la cantidad de elementos de esta (y por lo tanto de cualquier) base. Es decir, si B = v
1
, . . . , v
n
es una base de E, entonces
dimE = n.
Teorema 4. Sea E un espacio de dimension nita.
a) Todo conjunto de generadores de E contiene una base.
b) Todo conjunto de vectores L.I. de E esta contenido en una base de E.
c) Si S es un subespacio vectorial de E, entonces S es de dimension nita y dim(S) dim(E).
Mas a un, si dim(S) = dim(E), entonces S = E.
4 Normas Vectoriales y Ortogonalidad
4.1 Normas Vectoriales
Sea E un espacio vectorial real. Una norma sobre E es una funcion | | : E R que satisface las
siguientes propiedades. Si x, y E y c R:
i) |x| 0, y |x| = 0 si y solo si x = 0.
ii) |x +y| |x| +|y|.
iii) |cx| = [c[ |x|.
Un vector unitario (con respecto a | |) es un vector x E tal que |x| = 1.
Ejemplo. En E = R
n
, las p-normas son denidas de la siguiente manera. Si x = (x
1
, . . . , x
n
) R
n
:
1. Norma de la suma: |x|
1
=
n
i=1
[x
i
[.
2. Norma euclidiana: |x|
2
=
i=1
[x
i
[
2
1/2
.
3. Norma del maximo: |x|
= max
1in
[x
i
[.
7
4. p-norma: Si p 1, |x|
p
=
i=1
[x
i
[
p
1/p
.
Se dice que dos normas | |
a
, | |
b
sobre el mismo espacio vectorial E son equivalentes, si existen
constantes c
1
, c
2
> 0, tales que
c
1
|x|
a
|x|
b
c
2
|x|
a
, para todo vector x en E .
Teorema 5. En el espacio vectorial R
n
, todas las normas son equivalentes.
Ejemplo. Para todo vector x R
n
se cumple que:
|x|
2
|x|
1
n|x|
2
,
|x|
|x|
2
n|x|
,
|x|
|x|
1
n|x|
.
4.2 Producto Interno
Un producto interno o producto escalar sobre el E.V. real E es una funcion , : E E R
que satisface las siguientes propiedades. Si u, v, w E, y R,
Simetra: u, v = v, u.
Bilinearidad: u +v, w = u, w +v, w , u, v = u, v ,
u, v +w = u, v +u, w , u, v = u, v .
Positividad: Si u ,= 0, entonces u, u > 0.
Es decir, un producto interno es un funcional bilineal simetrico denido positivo sobre E.
Observaciones: A partir de las propiedades anteriores, podemos deducir las siguientes. Sean u, v
vectores de E.
u, 0 = 0, u = 0.
u = 0 si y solamente si u, w = 0 para todo w E.
u = v si y solamente si u, w = v, w para todo w E.
La funcion u |u| := u, u
1/2
dene una norma sobre E.
Desigualdad de Schwarz. [u, v[ |u| |v|, y la igualdad vale si y solo si uno de estos
vectores es m ultiplo del otro.
Si u, v son vectores de E, el producto interno u, v tambien es denotado por u v.
Ejemplos.
1. En el espacio euclidiano R
n
, si u = (
1
, . . . ,
n
), v = (
1
, . . . ,
n
) son vectores de R
n
, el producto
interno canonico de estos vectores es denido por
u, v :=
1
1
+
n
n
.
8
La norma asociada a este producto interno es la norma euclidiana ||
2
.
En este caso, el coseno del angulo formado por los vectores u, v R
n
es
cos =
u, v
|u|
2
|v|
2
.
En particular, el angulo formado entre los vectores u, v E es = 90
, cuando u, v = 0.
2. Sea E = C([a, b], R). Un producto interno en E es el siguiente:
f, g =
b
a
f(x)g(x) dx.
Sea , un producto interno sobre el espacio vectoria real E. Se dice que los vectores u, v E son
ortogonales o perpendiculares cuando u, v = 0.
Se dice que dos conjuntos X, Y de vectores en E son ortogonales cuando todo vector x X es
ortogonal a todo vector y Y .
Un conjunto X de vectores no nulos de E es llamado ortogonal cuando cualesquiera dos vectores
distintos en X son ortogonales. Si adicionalmente, todo vector de X es unitario, diremos que X es
ortonormal.
Diremos que B es una base ortonormal de E si B es ortonormal y es tambien una base de E.
Ejercicios. Sea E un espacio vectorial con producto interno.
1. Pruebe que los vectores de un conjunto ortogonal S de E son linealmente independientes.
2. Sean X = v
1
, v
2
, . . . , v
m
y Y = u
1
, u
2
, . . . , u
n
conjuntos de vectores de E tales que, para
cada i = 1, 2, . . . , m y cada j = 1, 2, . . . , n, los vectores v
i
y u
j
son ortogonales. Pruebe que los
conjuntos span(X) y span(Y ) son ortogonales.
3. (Proceso de Grand-Schmidt) Sean v
1
, v
2
, . . . , v
m
vectores L.I. de E. Efect ue el siguiente algo-
ritmo:
Para k = 1: Hacer u
1
=
v
1
v
1
.
Para k = 2, 3, . . . , m: Hacer w
k
= v
k
k1
i=1
v
k
, u
i
u
i
y luego u
k
=
w
k
w
k
.
a) Pruebe que el algoritmo esta bien denido.
b) Pruebe que el conjunto U = u
1
, u
2
, . . . , u
m
es ortonormal.
c) Pruebe que, para cada k = 1, 2, . . . , m, span(v
1
, v
2
, . . . v
k
) = span(u
1
, u
2
, . . . , u
k
).
d) Pruebe que si los vectores v
1
, v
2
, . . . , v
m
fueran L.D. entonces el proceso se truncara antes
de terminar.
9
Potrebbero piacerti anche
- Algoritmos: análisis, diseño e implementaciónDa EverandAlgoritmos: análisis, diseño e implementaciónNessuna valutazione finora
- Espacio VectorialDocumento13 pagineEspacio VectorialCelestino VargasNessuna valutazione finora
- Espacios VectorialesDocumento11 pagineEspacios Vectorialesapi-3746112100% (6)
- Problemas resueltos de electromagnetismo. Volumen I: ElectrostáticaDa EverandProblemas resueltos de electromagnetismo. Volumen I: ElectrostáticaNessuna valutazione finora
- Vectores AlgebraDocumento15 pagineVectores AlgebraJunior Hinojosa SuaresNessuna valutazione finora
- Curso básico de teoría de númerosDa EverandCurso básico de teoría de númerosValutazione: 5 su 5 stelle5/5 (2)
- Funciones Exponenciales y LogarítmicasDocumento16 pagineFunciones Exponenciales y LogarítmicasJuan ChrNessuna valutazione finora
- ApuntesMDI PDFDocumento215 pagineApuntesMDI PDFJoséNessuna valutazione finora
- 1-Espacios VectorialesDocumento3 pagine1-Espacios VectorialesPablo Ballesteros RodríguezNessuna valutazione finora
- Espacios VectorialesDocumento14 pagineEspacios VectorialesJose VeronaNessuna valutazione finora
- Espacio VectorialDocumento15 pagineEspacio VectorialAlberto Perez RodriguezNessuna valutazione finora
- Espvectorial 1Documento6 pagineEspvectorial 1JORGE ENRIQUE GOMEZ MEDINANessuna valutazione finora
- Teoria de Espacios Vectoriales y Aplicaciones LinealesDocumento12 pagineTeoria de Espacios Vectoriales y Aplicaciones LinealesJ.A VNessuna valutazione finora
- Espacio Vectorial y Subespacio VectorialDocumento8 pagineEspacio Vectorial y Subespacio VectorialRafael CórdovaNessuna valutazione finora
- Algebra LinealDocumento21 pagineAlgebra LinealRaul B. ReyesNessuna valutazione finora
- Documento 1Documento16 pagineDocumento 1Maria Fernanda Meza TapiaNessuna valutazione finora
- Algebra LinealDocumento14 pagineAlgebra LinealCarol KristiNessuna valutazione finora
- Carolina Becerra - Apuntes de Algebra LinealDocumento98 pagineCarolina Becerra - Apuntes de Algebra LinealCristian Muñoz JeldresNessuna valutazione finora
- Matemáticas ENMDocumento258 pagineMatemáticas ENMfguzcre100% (1)
- ESPACIOS VECTORIALES Álgebra LinealDocumento30 pagineESPACIOS VECTORIALES Álgebra LinealAmIn20122100% (1)
- Espacios VectorialesDocumento15 pagineEspacios Vectorialesvictor manuel vergara duarteNessuna valutazione finora
- A1tema3 0809 PDFDocumento15 pagineA1tema3 0809 PDFJhymer Josue Alvariño CosarNessuna valutazione finora
- Espacios VectorialesDocumento26 pagineEspacios VectorialesRaquelAbigailJerónimoNessuna valutazione finora
- Espacios VectorialesDocumento5 pagineEspacios VectorialesLaudino Vega ValenciaNessuna valutazione finora
- APUNTES Mat1203Documento51 pagineAPUNTES Mat1203Oscar CastilloNessuna valutazione finora
- Espacios Vectoriales Reales.Documento13 pagineEspacios Vectoriales Reales.AMYNNXXXXNessuna valutazione finora
- Espacios Vectoriales S11Documento19 pagineEspacios Vectoriales S11ce.david14Nessuna valutazione finora
- Algebra LinealDocumento24 pagineAlgebra LinealRaul B. ReyesNessuna valutazione finora
- Operaciones Con Sub Espacios VectorialesDocumento13 pagineOperaciones Con Sub Espacios VectorialesJosé PazNessuna valutazione finora
- Semana 4Documento15 pagineSemana 4josse obandoNessuna valutazione finora
- Unidad 4 PDFDocumento23 pagineUnidad 4 PDFAndrea Haro GonzalezNessuna valutazione finora
- Capitulo 9Documento28 pagineCapitulo 9Jose Eduardo Barriga RuaNessuna valutazione finora
- Portafolio de Evidencia Unidad 4Documento12 paginePortafolio de Evidencia Unidad 4Alejandro BosquezNessuna valutazione finora
- Espacios VectorialesDocumento17 pagineEspacios VectorialesEsau osorioNessuna valutazione finora
- Problemas Resueltos de Teorc3ada de ColasDocumento15 pagineProblemas Resueltos de Teorc3ada de ColasTeresa AguilarNessuna valutazione finora
- Algebra ApuntesDocumento6 pagineAlgebra ApuntesDavid Nicolás Vega PáezNessuna valutazione finora
- 00cap 2 Dependencia e Independencia Lineal, Base y DimensionDocumento36 pagine00cap 2 Dependencia e Independencia Lineal, Base y Dimensioneli2013Nessuna valutazione finora
- Apuntes de Algebra 2 Ma - 290 Corregido - 2 PDFDocumento107 pagineApuntes de Algebra 2 Ma - 290 Corregido - 2 PDFFranco Araya CortesNessuna valutazione finora
- Espacio VectorialDocumento6 pagineEspacio VectorialManolo DamascoNessuna valutazione finora
- Unidad I Calculo IIIDocumento32 pagineUnidad I Calculo IIIjongualjosescribdNessuna valutazione finora
- Resumen - Tema - 3 - Espacios VectorialesDocumento7 pagineResumen - Tema - 3 - Espacios VectorialesDaniel GonzaloNessuna valutazione finora
- Sistemas de Ecuaciones Lineales y MatricesDocumento32 pagineSistemas de Ecuaciones Lineales y MatricesFranco MoranNessuna valutazione finora
- Espacio S Vectorial Es 0809Documento16 pagineEspacio S Vectorial Es 0809CAMPONessuna valutazione finora
- Presentación de PowerPointDocumento39 paginePresentación de PowerPointeducas1Nessuna valutazione finora
- Espacios VectorialesDocumento67 pagineEspacios VectorialesGabriela Mayorga Sanchez50% (2)
- Espacios VectorialesDocumento14 pagineEspacios VectorialesgdlcnmarNessuna valutazione finora
- Algebra LinealDocumento11 pagineAlgebra LinealAPCNessuna valutazione finora
- Resumen Unidad 4Documento6 pagineResumen Unidad 4FedrickNessuna valutazione finora
- 07 - Espacios VectorialesDocumento21 pagine07 - Espacios VectorialesSebastian VeraNessuna valutazione finora
- Apuntes As Lade (Algebra Lineal) Curso 2005-2006Documento45 pagineApuntes As Lade (Algebra Lineal) Curso 2005-2006Gabi Recinos Sandoval100% (1)
- Espacio S Vectorial EsDocumento12 pagineEspacio S Vectorial EsFrancisco SanchezNessuna valutazione finora
- Quimicas en BeamerDocumento23 pagineQuimicas en Beamerbruenor304amancaboihNessuna valutazione finora
- Espacios VectorialesDocumento16 pagineEspacios VectorialesTefa De la TorreNessuna valutazione finora
- Algebra LinealDocumento13 pagineAlgebra LinealVerónicaNessuna valutazione finora
- Clase 4Documento5 pagineClase 4Dash AcuarioNessuna valutazione finora
- 001 Algebra LinealDocumento241 pagine001 Algebra LinealEnric Ruiz VazquezNessuna valutazione finora
- Sobre Nilálgebras Conmutativas de Potencias AsociativasDa EverandSobre Nilálgebras Conmutativas de Potencias AsociativasNessuna valutazione finora
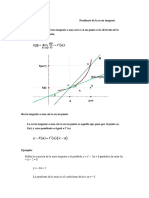
- Ajuste de Curvas Polinomios de Regresion Interpolacion de Newton Interpolacion de LagrangeDocumento5 pagineAjuste de Curvas Polinomios de Regresion Interpolacion de Newton Interpolacion de LagrangeShoni IsraelNessuna valutazione finora
- Topología (15versión)Documento61 pagineTopología (15versión)Angie CastilloNessuna valutazione finora
- Método de Ortogonalización Gram-Schmidt PDFDocumento7 pagineMétodo de Ortogonalización Gram-Schmidt PDFIvan Acuña GilNessuna valutazione finora
- Ecuaciones Cuadraticas Lineales Word Imprimir1Documento12 pagineEcuaciones Cuadraticas Lineales Word Imprimir1Jessik CruzNessuna valutazione finora
- Φ8 HOMEOMORFISMOSDocumento2 pagineΦ8 HOMEOMORFISMOSLuna Beth AlarconNessuna valutazione finora
- Apuntes Algebra Lineal CompletoDocumento89 pagineApuntes Algebra Lineal CompletoOscar Mendiola SoteloNessuna valutazione finora
- Guía Nº 2 - Geometría AnalíticaDocumento8 pagineGuía Nº 2 - Geometría AnalíticaPepe Salazar DiazNessuna valutazione finora
- Los Números EnterosDocumento7 pagineLos Números EnterosAmIn20122Nessuna valutazione finora
- Sistemas 2X2 PDFDocumento13 pagineSistemas 2X2 PDFCarol RiosNessuna valutazione finora
- Tabla de IntegralesDocumento5 pagineTabla de IntegralesMariaJoseHansen-vikGomezNessuna valutazione finora
- Representación de GrupoDocumento5 pagineRepresentación de GrupoJavier Garcia RajoyNessuna valutazione finora
- TALLER APLICATIVO 1 Matematicas Fundamentales AEMDDocumento4 pagineTALLER APLICATIVO 1 Matematicas Fundamentales AEMDEdwin Esneider GALINDO BELTRANNessuna valutazione finora
- C2 - Parte 1 - RectaDocumento13 pagineC2 - Parte 1 - RectaMilton Alejandro CuencaNessuna valutazione finora
- UNIDADES DE APRENDIZAJE AUTOÌ - NOMO PENSAMIENTO MATEMAÌ - TICO ALEdits 18 JunDocumento134 pagineUNIDADES DE APRENDIZAJE AUTOÌ - NOMO PENSAMIENTO MATEMAÌ - TICO ALEdits 18 JunantonioNessuna valutazione finora
- Sistemas de Segundo OrdenDocumento17 pagineSistemas de Segundo OrdenOrlando FernandezNessuna valutazione finora
- Complementos de CalculoDocumento1 paginaComplementos de CalculoDavid AndradeNessuna valutazione finora
- Pendiente de La Recta TangenteDocumento9 paginePendiente de La Recta TangenteJairo IsraelNessuna valutazione finora
- Programacion ModularDocumento47 pagineProgramacion ModularAlejandra Rivera ChaverraNessuna valutazione finora
- Tema 3 - Variables Aleatorias IDocumento22 pagineTema 3 - Variables Aleatorias IFernando Brugarolas navarroNessuna valutazione finora
- Rectas y PlanosDocumento15 pagineRectas y PlanosThomas NuñoNessuna valutazione finora
- Distribución HipergeométricaDocumento3 pagineDistribución HipergeométricaPaz ZitaNessuna valutazione finora
- 2trabajo Practico N 8 Sistemas de Ecuaciones LinealesDocumento5 pagine2trabajo Practico N 8 Sistemas de Ecuaciones LinealesPaula MorenoNessuna valutazione finora
- Ep 2018-1 C. IntegralDocumento8 pagineEp 2018-1 C. IntegralAgustin GonzalesNessuna valutazione finora
- Estabilidad NyquistDocumento15 pagineEstabilidad NyquistJuanNessuna valutazione finora
- Exammate2015 MaestriaDocumento4 pagineExammate2015 MaestriaFrancisco BenítezNessuna valutazione finora
- Deduccion de La Ecuacion de EulerDocumento4 pagineDeduccion de La Ecuacion de EulerPool Ankori QuilcaNessuna valutazione finora
- Algebra Lineal - Rango y Base - EjemplosDocumento3 pagineAlgebra Lineal - Rango y Base - EjemplosRené ChapaNessuna valutazione finora
- 95 - Fase 4 - TrabajoDocumento14 pagine95 - Fase 4 - TrabajoJessika SuAlvaNessuna valutazione finora