Presented by APN Rao, Dept ECE, GRIET, Hyderabad.

Aug 2011 1
Fourier Series &
Fourier Transform
www.jntuworld.com
JBJ Fourier (1768- 1830)
2
A product of the French Revolution,
(Jean Baptiste) Joseph Fourier held positions
within the Napoleonic Empire during his
early career. After Napoleons fall from
power, Fourier devoted his talents
exclusively to science. Although he won
the Institut de France prize in 1811 for
his work on heat diffusion, criticism of its
mathematical rigor and generality led him to
publish the classic book Thorie analytique de
la chaleur in 1823. Within this book he
introduced the world to the series that
bears his name.
Presented by APN Rao, Dept ECE, GRIET, Hyderabad. Aug 2011
www.jntuworld.com
3
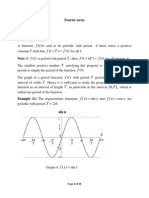
Trigonometric Fourier Series
Orthogonality Check
0 0
0
0 0
0
cos cos for
2
0 for m n
cos sin 0 for all m,n
T
T
T
m t n t dt m n
m t n t dt
e e
e e
= =
=
=
}
}
0 0
0
0 0
sin sin for
2
= 0 for m n
1 is orthogonal to cos andsin
for all n
T
T
m t n t dt m n
n t n t
e e
e e
= =
=
}
Orthogonal Basis Set
cos n
0
t, sin n
0
t, 1;
n= 1,2,
Presented by APN Rao, Dept ECE, GRIET, Hyderabad. Aug 2011
www.jntuworld.com
4
Trigonometric Series of Periodic Signals
| |
0 0 0
1
0
0
0
0 0
0 0
( ) cos sin
2
( ) periodic with ;
1
( ) ( )
2 2
( ) cos ; ( ) sin
n n
n
T
T T
n n
f t a a n t b n t
where f t T
a f t dt average value of f t
T
a f t n t dt b f t n t dt
T T
e e
t
e
e e

=
= + +
=
= =
= =

}
} }
Trigonometric Fourier series can exactly represent a continuous
waveform over an interval (t
1
,t
2
), with fundamental period T equal
to the specified interval. However, as the basis functions are
periodic with their periods having integer ratios, their sum is
periodic with period T. Thus trigonometric series are naturally
suited for representing periodic signals.
Presented by APN Rao, Dept ECE, GRIET, Hyderabad. Aug 2011
www.jntuworld.com
5
Trigonometric Series: Examples
0 - 2 3
0 /2 -/2 3/2
0 1 -1 2 3
0 T -T 2T 3T
1
-1
1
1
A
-1
4 4 4
sin sin3 sin5 .....
3 5
t t t
t t t
= + + +
0 0
0
2 4 4
cos cos2
3 15
4
cos3 .....
35
t t
t
e e
t t t
e
t
=

2 2 2
2
8 8 8
sin sin3 sin5
9 25
8
sin7 .....
49
t t t
t
t t t
t
= +
+
sin2 sin4
2 2
sin6 .....
3
A A A
t t
A
t
t t
t t
t
t
=

square wave
full wave rectified sine wave
triangular wave
sawtooth wave
t
t
t
t
Presented by APN Rao, Dept ECE, GRIET, Hyderabad. Aug 2011
www.jntuworld.com
6
Trigonometric Fourier Series: Useful Observations
Presented by APN Rao, Dept ECE, GRIET, Hyderabad. Aug 2011
f(t) with even symmetry does not have sine components.
f(t) with odd symmetry has no cosine components and no constant
term.
f(t) with half-wave symmetry does not have even harmonics.
Constant (dc) term hides odd symmetry.
A shift in origin of f(t) changes coefficients of both sine and cosine
terms.
Enables view of a periodic signal in terms of its harmonic content,
which becomes equivalent description of the signal in frequency
domain. Frequency domain plots (of a
n
s and b
n
s) or spectra would be
discrete, with values specified only at multiples of fundamental
frequency.
Amplitude scaling of f(t) causes scaling of all components by same
factor.
Compression in time causes expansion in frequency, and vice versa.
Time shift of f(t) requires each harmonic to be phase-shifted by a
value proportional to its frequency i.e., time-delay of t
0
in f(t) causes
phase of n
th
harmonic to lag by n
0
t
0.
www.jntuworld.com
7
1 0
( ) sin( ) f t t e =
2 0
( ) sin(2 ) f t t e =
3 1 2 0 0
( ) ( ) ( ) sin( ) sin(2 ) f t f t f t t t e e = + = +
t
t
t
Periodic Waveshape as Sum of Harmonics: Example
Presented by APN Rao, Dept ECE, GRIET, Hyderabad. Aug 2011
www.jntuworld.com
8
Harmonic Content of Audio Waveforms (1 KHz)
Factory Whistle
Soprano
Piano
Presented by APN Rao, Dept ECE, GRIET, Hyderabad. Aug 2011
www.jntuworld.com
9
Complex Exponential Fourier Series
Orthogonality Check
( )
0 0
0
for

0 for
T
jm t jn t
T m n
e e dt
m n
e e
- =

=

=

}
Orthogonal Basis Set
Obtaining Exponential Series
0 0
0
1
( ) , ( )
T
jn t jn t
n n
n
f t F e where F f t e dt
T
e e

=
= =

}
Presented by APN Rao, Dept ECE, GRIET, Hyderabad. Aug 2011
0
0, 1, 2,...
:
jn t
n
e
e
=
www.jntuworld.com
10 Presented by APN Rao, Dept ECE, GRIET, Hyderabad. Aug 2011
Complex Exponential Series: Examples
0 - 2 3
0 /2 -/2 3/2
0 1 -1 2 3
0 T -T 2T 3T
1
-1
1
1
A
-1
square wave
full wave rectified sine wave
triangular wave
sawtooth wave
t
t
t
5 3
3 5
2 2 2
...
5 3
2 2 2
...
3 5
j t j t jt
jt j t j t
j e j e j e
j e j e j e
t t t
t t t

= + + +

0 0 0
0 0 0
3 2
2 3
2 2 2 2
...
35 15 3
2 2 2
...
3 15 35
j t j t j t
j t j t j t
e e e
e e e
e e e
e e e
t t t t
t t t

= + + + +

5 3
2 2 2
3 5
2 2 2
4 4 4
...
25 9
4 4 4
...
9 25
j t j t jt
jt j t j t
e e j e
j e e e
t t t
t t t

= + +
+ +
4 2
2 4
...
4 2 2
...
2 4
j t j t
j t j t
jA jA A
e e
jA jA
e e
t t
t t
t t
t t

= +
+ + +
www.jntuworld.com
11
Relation with Trigonometric Series
Presented by APN Rao, Dept ECE, GRIET, Hyderabad. Aug 2011
( )
;
2 2 2 2
;
n n n n
n n
n n n n n n
a b a b
F j F j
a F F b j F F

= = +
= + =
Some Notes on Complex Exponential Fourier Series
2
For periodic f(t), average power ( ' )
For signal f(t),
(conjugate symmetry)
(magnitude spectrum even)
and (phase spectrum odd)
n
n n
n n
n n
F Parseval s relation
real valued
F F
F F
F F

=
=
=
Z = Z

Negative frequency is only a mathematical concept and has no

physical meaning.
www.jntuworld.com
12
Extending Exponential Series of Periodic Signal f
p
(t)
to obtain Fourier Transform of Aperiodic Signal f(t)
Presented by APN Rao, Dept ECE, GRIET, Hyderabad. Aug 2011
0
0
2
2
0
0
2
0
2
( ) ( )
( ) ( )
(Analysis Equation
Let ( ) lim ( )
1
( )
2
, 0
, ( ) ( )
)
p
T
T
j
T
j
n t
n p
T
n t
n p
T
j
p
t
f t f t
F f t e dt
T
as
F n F T f t e dt
F f t e
T
T
n n f t f t
dt
e
e
e
t
e e
e
e
e
e e

=
=
= A =

=
=
= A

}
}
}

0
0
0
0
0
0
0
0
0
( )
( ) ; using
( )
=

1
(
= ( )
2
1
= ( )
2
2
as , 0
, ( ) ( )
)
,
) (
2
n
jn t
p n n
n
n
n
n
n
n
n
p
j
jn t
jn t
jn t
F n
f t F e F
T
F n
T
F n
F n
f t
T
T
n n f t f
F
t
e
e
e
e
e
e
e
e
e
e
e
e
e
e
t
e e
t
e
t
e e
e e e
t
=
=
=
=
=
=
=
A =
A
= =
A A
= A =
= A
=

}
(Synthesis Equation)
t
de

}
( ) is th e of ( ) spectral density function F f t e
www.jntuworld.com
13
Dirichlets Conditions
Presented by APN Rao, Dept ECE, GRIET, Hyderabad. Aug 2011
Sufficient conditions to be satisfied by a periodic signal for existence
and convergence of fourier series:
absolute integrable over one period (weak condition)
no more than finite number of maxima and minima in a period
(strong condition)
no more than finite number of discontinuities in a period, and each
discontinuity must be finite (strong condition)
Sufficient conditions to be satisfied by a signal for existence of fourier
transform:
absolute integrable (weak condition)
no more than finite number of maxima and minima in any finite
interval (strong condition)
no more than finite number of discontinuities in any finite interval,
and each discontinuity must be finite (strong condition)
www.jntuworld.com
14
Fourier Transforms of Some Functions
Presented by APN Rao, Dept ECE, GRIET, Hyderabad. Aug 2011
( )
2 2
2

2
0
2
1 2
( ) 0; 0; ( ) 1
1
( ) 0; ( )
2
a t at
at
A t
t
a
e u t a e a t
a j a
te u t a f t A Sa
a j
t
t
o
e e
et
t
e

s
>
> >
+ +

| |
> =

|
\ . +

F F F
F F
( ) ( )
( ) ( ) ( ) { }
( ) ( ) { }
( ) ( )
0
0 0 0 0
0 0 0
0
1 2
2 ; ( ) ; sgn( )
2 ;cos
sin
Periodic function 2
j t
p n
n
A A u t t
j j
e t
t j
f t F n
e
t o e to e
e e
to e e e t o e e o e e
e t o e e o e e
t o e e

=
+
+ +
+

F F F
F F
F
F
www.jntuworld.com
15
Properties of Fourier Transforms (1/2)
Presented by APN Rao, Dept ECE, GRIET, Hyderabad. Aug 2011
0
0
1 1 2 2 1 1 2 2
0
0
1. Linearity: ( ) ( ) ( ) ( )
2. Time shift: ( ) ( )
3. Frequency shift: ( ) ( )
1
4. Time and frequency scaling: ( )
5. Time and frequency reversal:
j t
j t
a f t a f t a F a F
f t t F e
f t e F
f at F
a a
f
e
e
e e
e
e e
e

+ +


(

(

F
F
F
F
( )
1 2 1 2
1 2 1 2
( ) ( )
( )
6. Time differentiation: ( )
( )
7. Frequency differentiation: ( ) ( )
8. Time convolution: ( ) ( ) ( ) ( )
1
9. Frequency convolution: ( ) ( ) ( ) (
2
n
n
n
n
n
n
t F
d f t
j F
dt
d F
jt f t
d
f t f t F F
f t f t F F
e
e e
e
e
e e
e e
t

-
-
F
F
F
F
F
)
www.jntuworld.com
16
Properties of Fourier Transforms (2/2)
Presented by APN Rao, Dept ECE, GRIET, Hyderabad. Aug 2011
( )
10. Conjugation: ( ) ( )
for real ( ), ( ) = ( )
for real even ( ), ( ) is real; for real odd ( ), ( ) is imaginary
( )
11. Time integration: ( ) (0) ( )
1
t
f t F
f t F F conjugate symmetry
f t F f t F
F
f d F
j
e
e e
e e
e
t t t o e
e
- -
-

+
}
F
F
2
1
2. Frequency integration: ( ) (0) ( ) ( )
( )
13. Duality/symmetry: ( ) 2 ( ); ( )
2
1
14. Area relations: (0) ( ) ; (0) ( )
2
15. Parseval energy theorem: ( )
f t f t F d
jt
F t
F t f f
F f t dt f F d
f t dt
e
t o
t e e
t
e e
t

= =
}
} }
}
F
F F
2 1
( )
2
1
Generalized Parseval's relation: ( ) ( ) ( ) ( )
2
F d
f t g t dt F G d
e e
t
e e e
t

- -

=
=
}
} }
www.jntuworld.com
17
Properties of Fourier Transforms: Hints for Proofs
Presented by APN Rao, Dept ECE, GRIET, Hyderabad. Aug 2011
1. Direct consequence of linearity of integral operations
2. Change of variable from t to (t- t
0
) in synthesis equation
3. Change of variable from to (-
0
) in analysis equation
4. Change of variable in fourier transform of f(at)
5. Substitute a = -1 in property 4
6. Differentiate synthesis equation with respect to t
7. Differentiate analysis equation with respect to
8. Use convolution integral, replace either function from synthesis equation,
reverse order of integration. Then use analysis equation twice
9. Proceed in a similar manner as for property 8
10. Conjugate analysis equation, reverse sign of for main property. Apply for
real signals f(t) = f
*
(t), for real even f(t) = f(-t) and for real odd f(t) = -f(-t)
11. Note that LHS = f(t)*u(t). Use property 8 and FT of u(t) to obtain RHS
12. Obtain inverse transform of u() using property 13. Then proceed in similar
manner to that of property 11.
13. In synthesis equation change variable to and reverse its sign. Similar
operations in analysis equation for second part
14. Obtain f(0) from synthesis and F(0) from analysis equations
15.
2
( ) ( ) ( ), for ( ) use conjugate of synthesi s equation, then
reverse order of integration.
f t f t f t f t
- -
=
www.jntuworld.com
18
Some More Fourier Transform Pairs
Presented by APN Rao, Dept ECE, GRIET, Hyderabad. Aug 2011
f(t) F()
|t|
2
2
e

0
sin ( )
at
e t u t e

( )
0
2
2
0
a j
e
e e + +
1
0
t
t
t
t
t
t
<
<
2
2
Sa
et
t
(
| |
|
(
\ .

( )
1
( )
1 !
n
at
t
e u t
n

( )
1
n
a je +
( )
2
2
t
e
t
( )
2
2
2
t
e
t
t t

2 2
w wt
Sa
t
| |
|
\ .
1
2
0
2
w
w
e
e
<
>
www.jntuworld.com
19
Some Interesting Correspondences between
Operations on Fourier Transform Pairs
Presented by APN Rao, Dept ECE, GRIET, Hyderabad. Aug 2011
One Domain Other Domain
Convolution Multiplication
Compression Expansion
Periodicity
(Repetition)
Discreteness
(Sampling)
Even-odd split Real-imaginary split
Shift Multiply by complex exponential
Differentiation Multiply by domain variable and j
Integration Divide by domain variable and j, + impulse at origin
Conjugation Conjugation with sign reversed domain variable
Analytical form Single-sidedness (causal/anti-causal)
www.jntuworld.com
20
Energy Spectral density S
f
()
Presented by APN Rao, Dept ECE, GRIET, Hyderabad. Aug 2011
Based on Parseval's energy theorem, we can perceive energy distribution in frequency
domain and accordingly define a useful quantity called Energy Spectral Density:

2
( )
( )
2
1) ( ) 0 ; esd is real and non-negative
2) ( ) ( ); for a real sign
Properties
al, esd is
of Energy Spec
even function
tral
of
3) Energy ( )
Density
f
f
f f
f f
F
S
S
S S
E S d
e
e
t
e
e e e
e e

>
=
=
}

1 2
1 2
12
From generalized Parseval's theorem, we define cross-energy spectral density of
two signals f ( ) and f ( )
( ) ( )
( ) ; (generally complex)
2
t t
F F
S
e e
e
t
-

Cross Energy Spectral density

www.jntuworld.com
21
Power Spectral density P
f
()
Presented by APN Rao, Dept ECE, GRIET, Hyderabad. Aug 2011
2
Power signals in general do not have fourier transforms. However, they can be described in
frequency domain in terms of defined as below:
( )
1
P ( ) lim , where ( ) is

e
2

th
T
f T
T
F
F
T
power spectral density
e
e e
t

=
2
FT of power signal ( ) trucated to interval T
( )
1
: is the of the truncated power signal
2
T
mean energy spectral densi
f t
F
no y t t e
T
e
t
(
(
(

:
1. ( ) real and 0 2. ( ) ( ) for real ( )
3. of ( ) =
Properties of power spectral density
( )
f f f
f
P P P f t
Average Power f t P d
e e e
e e

> =
}
Cross Power Spectral density
1 2
1 2
12
We define cross-power spectral density of two signals f ( ) and f ( ) as
( ) ( ) 1
( ) lim ; (generally complex)
2
T
t t
F F
P
T
e e
e
t
-

www.jntuworld.com
22 Presented by APN Rao, Dept ECE, GRIET, Hyderabad. Aug 2011
Concept of Signal Bandwidth
Frequency band over which a signal has significant spectral density can be
observed from its magnitude spectrum. If maximum spectral density is at zero
frequency, signal is said to be lowpass; and if at a non-zero frequency it is
bandpass.
Half-power (or 3 dB) bandwidth
for a low pass signal is |0-
c
| where
for a bandpass filter with maximum gain at
c
, it is |
1

2
| where

1
<
c
<
2
and
( ) (0) / 2
c
F F e =
1 2
( ) ( ) ( ) / 2
c
F F F e e e = =
Pulse width Bandwidth Relation
Pulse width may be defined as the interval between the two half power
instants on either side of the peak (similar in concept to half power
bandwidth). Due to a property of Fourier Transform, an inverse relation
exists between pulse width and bandwidth of a signal. That is, narrow pulses
have large bandwidths and vice versa. We also state this relation
alternatively as pulse width x bandwidth = constant.
www.jntuworld.com
23
Introduction to Hilbert Transform
Presented by APN Rao, Dept ECE, GRIET, Hyderabad. Aug 2011

0
( ) ( ); Hilbert transform does not change domain.
1 1 ( )
[ ( )] ( ) ( )
1
sg
Positive frequencies are phase shifted by -9
n( ), ( ) s
0 and negative
f
gn(
e
) ( )
r
f t f
f
f t f t f t d
t t
j F
t
j F
t
t
t
t t t
e e e e
t

= - =

=
}

F
H
H

0

quencies by +90 . Magnitude spectrum is unchanged.
( ) and ( ) have same energy and are .
(For proof of orthogonality, use generalised Parseval's relation)
Hilbert transform appli
mutually orthogonal f t f t

ed twice: ( ) = ( ) ( ) f t f t f t
| |
=
|
\ .

H
www.jntuworld.com
24
Some Hilbert Transform Pairs
Presented by APN Rao, Dept ECE, GRIET, Hyderabad. Aug 2011
constant zero
( )
f t

( ) f t
cos t e sin t e
sin t e cos t e
( ) t o
1
t t
1
t t
( ) t o
sin
( )
t
Sa t
t
=
1 cost
t

1
0
t a
t a
s

>

1
ln
t a
t a t
+

j t
e
e
sgn( )
j t
j e
e
e
2 2
; 0
a
a
a e
>
+
2 2
t
a e +
www.jntuworld.com