FUNCIONES DE DOS VARIABLES

1- Funciones de dos variables reales

2- Lmites
3- Continuidad de funciones de dos variables
4- Derivabilidad de funciones de dos variables
5- Diferenciabilidad de funciones de dos variables
6- Derivada direccional. Vector gradiente
7- Derivada de la funcin compuesta. Regla de la cadena
8- Derivadas parciales de orden superior
9- Funciones implcitas
10- Extremos de funciones de dos variables
11- Extremos de funciones de dos variables con ligaduras
FUNCIONES REALES DE DOS VARIABLES REALES
Definicin
Una funcin real de n variables reales es una aplicacin
f: D
n
que hace corresponder a cada n-pla
(x
1
,x
2
,...,x
n
) e D un nmero real z e
f: D
n

(x
1
,x
2
,...,x
n
) z=f (x
1
,x
2
,...,x
n
)
Ejemplos: f :
3

(x
1
,x
2
,x
3
) z =
g:
2

g (x,y) z = 2x+3y
D= dominio de definicin de f
2
3
2
2
2
1
x x x + +
Para n=2
Una funcin real de dos variables reales es una aplicacin
f: D
2
que hace corresponder a cada par (x,y) e D un
nmero real z e
Ejemplos: f :
2

(x,y) z= x+xy
g :
2

(x,y) z= x
2
+e
2y
Representaciones grficas
Dado un sistema de referencia cartesiano
del espacio usual
3
de origen O y ejes X,Y y Z, el conjunto de puntos P
de coordenadas (x,y,f(x,y)), define una superficie en
3
denominada
representacin grfica de f.
O
X
Y
Z
P
z=f(x,y)
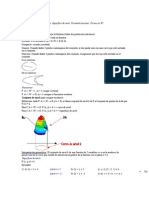
CURVAS DE NIVEL
Sea f: D
2

Definicin
Se llama curva de nivel m al conjunto
} m y) f(x, / D y) (x, { C
m
= =
El conjunto C
m
representa grficamente la proyeccin
ortogonal, sobre el plano z=0, de la interseccin de la
superficie de ecuacin z=f(x,y) y el plano horizontal de
ecuacin z=m.
LMITES
Sea f: D
2
y (x
0
,y
0
) un punto de acumulacin
de D
Definicin e es el lmite de f en el punto (x
0
,y
0
) si
se escribe:
No es necesario que la funcin est definida en el
punto x
0
sino en infinitos puntos a su alrededor
<
< + < > >

) y , x ( f
) y y ( ) x x ( 0 : D ) y , x ( / 0 0
2
0
2
0
=

) y , x ( f
lim
) y , x ( ) y , x (
0 0
O
X
Y
Z
z=f(x,y)
+ e

- e
(x
0
,y
0
)
Definicin
Se llaman lmites reiterados de f a los lmites definidos por:
si es que existen.
Proposicin
Si existe , es nico
Proposicin
Sean f y g dos funciones tales que:
1) f est acotada en un
entorno de (x
0
,y
0
)
2)
|

\
|

y) f(x, lim lim
0 0
x x y y
|

\
|

y) f(x, lim lim
0 0
y y x x
=

) y , x ( f
lim
) y , x ( ) y , x (
0 0
0 ) y , x ( g lim
) y , x ( ) y , x (
0 0
=

0 )] y , x ( g ) y , x ( f [ lim
) y , x ( ) y , x (
0 0
=

entonces,
Ejemplo: Calcular los lmites reiterados de la funcin
cuando (x,y)(0,0)
xy x y
f(x, y)
x y
+
=
+
1
x
x
lim
y x
y x xy
lim lim
0 x 0 y 0 x
=

=
(

+
+

1
y
y
lim
y x
y x xy
lim lim
0 y 0 x 0 y
= =
(

+
+

Proposicin
1) Para que exista el el valor
se debe obtener cualquiera que sea el camino
por el que nos acerquemos a (x
0
,y
0
)
2) Si existen y
es condicin necesaria para que exista el
que los lmites reiterados
coincidan y sean
|

\
|

y) f(x, lim lim
0 0
x x y y
|

\
|

y) f(x, lim lim
0 0
y y x x
=

) y , x ( f
lim
) y , x ( ) y , x (
0 0
=

) y , x ( f
lim
) y , x ( ) y , x (
0 0
Esto quiere decir que:
Si entonces
no existe
La funcin tiene lmites reiterados distintos en (0,0)
|

\
|

y) f(x, lim lim
0 0
x x y y
|

\
|

y) f(x, lim lim
0 0
y y x x
=

) y , x ( f
lim
) y , x ( ) y , x (
0 0
2 2
2
y x
y xy
) y , x ( f
+
+
=
1 1 lim
y
y
lim
y x
y xy
lim lim
0 0 lim
x
0
lim
y x
y xy
lim lim
0 y
2
2
0 y
2 2
2
0 x 0 y
0 x
2
0 x
2 2
2
0 y 0 x
= = =
(

+
+
= = =
(

+
+


Por tanto no existe el
2 2
2
) 0 , 0 ( ) y , x (
y x
y xy
lim
+
+

Puede ser que =

pero que no exista
La funcin tiene iguales los lmites reiterados en (0,0)
|

\
|

y) f(x, lim lim
0 0
x x y y
|

\
|

y) f(x, lim lim
0 0
y y x x
=

) y , x ( f
lim
) y , x ( ) y , x (
0 0
2 2
y x
xy
) y , x ( f
+
=
0 0 lim
y
0
lim
y x
xy
lim lim
0 0 lim
x
0
lim
y x
xy
lim lim
0 y
2
0 y
2 2
0 x 0 y
0 x
2
0 x
2 2
0 y 0 x
= = =
(

+
= = =
(

+


pero no existe el pues al hallarlo segn la
direccin y=mx queda:
2 2
) 0 , 0 ( ) y , x (
y x
xy
lim
+

2
0 x
2 2
2
0 x
2 2
0 x
2 2
mx y
) 0 , 0 ( ) y , x (
m 1
m
lim
) m 1 ( x
mx
lim
) mx ( x
) mx ( x
lim
y x
xy
lim
+
=
+
=
+
=
+

=

que depende de m
Puede existir sin que exista alguno o
ninguno de los lmites reiterados
La funcin tiene lmite en (0,0) pues es el
producto de una funcin que tiende a 0: x por otra funcin acotada
y por lo tanto
=

) y , x ( f
lim
) y , x ( ) y , x (
0 0
y
1
sen x ) y , x ( f =
y
1
sen
0
y
1
sen x lim
) 0 , 0 ( ) y , x (
=

Sin embargo
no existe pues no existe el
(

=
(

y
1
sen lim x lim
y
1
sen x lim lim
0 y 0 x 0 y 0 x
y
1
sen lim
0 y
Coordenadas polares de un punto
O x X
Y
y
P(x,y)
q
Cartesianas (x,y)
Polares ( r, q )
r
2 2
x y = +
y
arctg / ( , ]
x
=
Ecuaciones del cambio:
x=r cos q
y=r sen q
CONTINUIDAD
Sea f: D
2
y (x
0
,y
0
) un punto de D
Definicin
f es continua en el punto (x
0
,y
0
) si
Definicin
f es continua en un conjunto A D si es continua en cada punto de A
Proposicin
) y , x ( f ) y , x ( f
lim
0 0
) y , x ( ) y , x (
0 0
=

Si la funcin f es continua en (x
0
,y
0
), entonces existe un nmero
real tal que la funcin f est acotada en el conjunto D((x
0
,y
0
),d)D.
es decir, f est acotada en un entorno del punto (x
0
,y
0
)
0 >
Proposicin
Si dos funciones f y g son continuas en el punto (x
0
,y
0
), entonces las
funciones f+g, f-g y f.g son tambin funciones continuas en (x
0
,y
0
).
Adems, si g(x
0
,y
0
)0, entonces la funcin f/g es tambin una funcin
continua en (x
0
,y
0
).
DERIVABILIDAD
Sea f :D
n
y un punto perteneciente al
interior de D.
Definicin
Llamamos derivada parcial de f respecto de la i-sima variable en el
punto al lmite:
cuando existe y lo representamos por:

Definicin
f es derivable en el punto si existen las
derivadas parciales respecto de todas las variables en ese punto
) p ,...., p , (p p
n 2 1
=
) p ,...., p , (p p
n 2 1
=
h
) p ,..., p , p , p ,..., p , f(p ) p ,..., p h, p , p ,..., p , f(p
lim
n 1 i i 1 i 2 1 n 1 i i 1 i 2 1
0 h
+ +

+
) p (
x
f
i

) p f( D
i
x
) p f( D
i
) p ( f
i
x
) p ( f
i
) p ,...., p , (p p
n 2 1
=
Para hallar la derivada parcial respecto de la variable x
i:
en un punto , se deriva f respecto esa variable
considerando constantes el resto de las variables y posteriormente se
asignan los valores p
1
,p
2
,...,p
n
a las variables x
1
,x
2
,...,x
n
respectivamente.
Ejemplo: f(x,y,z)= x
3
z +x seny ln(x+z)
) p (
x
f
i

) p ,..., p , p ( p
n 2 1
=
]
2
1
2
1
1
z x
1
x ) 1 , 0 , 1 (
z
f
1 y cos x ) 1 , 0 , 1 (
y
f
2
5
2
1
3
z x
1
seny z x 3 ) 1 , 0 , 1 (
x
f
) 1 , 0 , 1 (
3
) 1 , 0 , 1 (
) 01 , 1 (
2
= =
(

(
+
=

= =

= =
(

(
+
+ =

Sea f :D
2
y un punto (x
0
,y
0
) perteneciente al
interior de D.
Las dos derivadas parciales de f en (x
0
,y
0
) estn
definidas por:
k
) y , x ( f ) k y , x ( f
lim ) y , x (
y
f
h
) y , x ( f ) y , h x ( f
lim ) y , x (
x
f
0 0 0 0
0 k
0 0
0 0 0 0
0 h
0 0
+
=

+
=

Esas derivadas parciales representan las pendientes de las

tangentes a las curvas C
1
y C
2
intersecciones de la
superficie de ecuacin z=f(x,y) con los planos de
ecuaciones respectivas y=y
0
y x=x
0
.
Para n=2
Definicin
Sea f :D
n
y un punto perteneciente a D.
Se denomina funcin derivada parcial de f respecto de la i-sima
variable denotada f
i
D
i
f , a la aplicacin
que hace corresponder a cada punto la derivada parcial de f respecto
de esa variable en .
Ejemplo: f(x,y,z)= x
3
z +x seny ln(x+z)
i
x
f

f D
i
x
i
x
f
) p ,...., p , (p p
n 2 1
=
p
p
z x
1
x
z
f
y cos x
y
f
z x
1
seny z x 3
x
f
3
2
+
=

+
+ =

Definicin
Sea f :D
n
y un punto perteneciente a D.
Se denomina funcin derivada parcial segunda de f respecto de las
variables x
i
y x
j
y se denota
, a la derivada parcial de respecto de la
variable x
j
en el punto .
) p (
x x
f
j i
2

) p f( D
j
x
i
x
) p ( f
j
x
i
x
) p ,...., p , (p p
n 2 1
=
p
) p ( f
ij
) p ( f D
ij
i
x
f

Anlogamente se definen las derivadas parciales de rdenes

superiores
Ejemplo: f(x,y,z)= x
3
z +x seny ln(x+z)
z x
1
x
z
f
y cos x
y
f
z x
1
seny z x 3
x
f
3
2
+
=

+
+ =

Hallar: en el punto (1,1,1)

2 2 3
2 2
f f f
, ,
x y x z x


]
4
23
) z x (
2
x 6
) z x (
1
x 3 D
z x
1
x D D
x z
f
4
25
) z x (
1
xz 6
z x
1
seny z x 3 D
x
f
1 cos y cos
z x
1
seny z x 3 D
y x
f
) 1 , 1 , 1 (
3
) 1 , 1 , 1 (
2
x
) 1 , 1 , 1 (
3
x x
2
3
) 1 , 1 , 1 (
2
) 1 , 1 , 1 (
2
x
2
2
) 1 , 1 , 1 (
) 1 , 1 , 1 (
2
y
2
2
=
(

(
+
=
|
|

\
|
+
+ =
|
|

\
|
|

\
|
+
=

=
(

(
+
+ =
|

\
|
+
+ =

= =
|

\
|
+
+ =

Proposicin
Si f y g son funciones derivables en el punto , entonces
f+g, f-g, f.g, tambin son derivables en y si
tambin lo es la funcin f/g.
Teorema de Schwarz
Sea f :D
2
y un punto (x
0
,y
0
) de D.
Si existen las derivadas parciales en un
entorno del punto (x
0
,y
0
) y es continua en (x
0
,y
0
),
entonces existe en el punto (x
0
,y
0
) y se
cumple que:
p
p 0 ) p ( g
y x
f
y
y
f
,
x
f
2

y x
f
2

x y
f
2

) y , x (
y x
f
) y , x (
x y
f
0 0
2
0 0
2

Ejemplo: f(x,y)= x
3
y
2
+3xy
4
-2y
2
y 4 xy 12 y x 2
y
f
y 3 y x 3
x
f
3 3
4 2 2
+ =

+ =

( )
( )
2
2 2 4 2 3
y
2
3 3 2 3
x
f
D 3x y 3y 6x y 12y
x y
f
D 2x y 12xy 4y 6x y 12y
y x

= + = +

= + = +

Coinciden "(x,y)
2
Definicin
Sea f :D
2

f es de clase C
m
en un abierto A D, si existen todas las
derivadas parciales hasta el orden m en A, y esas
derivadas parciales son continuas en A.
f es de clase C
m
en un punto si existe un abierto
A D tal que y f es de clase C
m
en A.
D p
A p
DIFERENCIALES
Sea f: D
2
y (x
0
,y
0
) un punto del interior de D
Definicin
f es diferenciable en (x
0
,y
0
) si existe una aplicacin lineal
L:
2
tal que:
Si f es diferenciable en (x
0
,y
0
) la aplicacin lineal L es
nica ,se llama diferencial de f en (x
0
,y
0
) y se representa
df (x
0
,y
0
)
0 0 0 0
2 2
(h,k) (0,0)
f (x h, y k) f (x , y ) L(h,k)
lim 0
h k

+ +
=
+
Proposicin
Si existen las derivadas parciales en un
entorno del punto (x
0
,y
0
) y son continuas en (x
0
,y
0
),
entonces f es diferenciable en el punto (x
0
,y
0
)
y
f
y
x
f

Si f es diferenciable se llama diferencial total de f a la

expresin:
Si f no es diferenciable esta expresin no tiene ningn
sentido
Se llaman diferenciales parciales de f a las expresiones:
x y
f f
d f dx, d f dy
x y

= =

f f
df dx dy
x y

= +

f f
df dx dy (2seny 6xy)dx (2xcosy 3x)dy
x y

= + = + + +

x
y
f
d f dx (2seny 6xy)dx
x
f
d f dy (2xcosy 3x)dy
y

= = +

= = +

Ejemplo: Calcular la diferencial total y las parciales de la

funcin
f(x,y)=2x seny + 3x
2
y
Proposicin
Si f y g son funciones diferenciables en el punto ,
entonces f+g, f-g, f.g, tambin son diferenciables en
y si tambin lo es la funcin f/g.
p
p
0 ) p ( g
Proposicin
Si f es diferenciable en (x
0
,y
0
) entonces f es continua y
derivable en (x
0
, y
0
)
!! f derivable f diferenciable !!
Proposicin
Sea z=f(x,y) la ecuacin de una superficie S definida en
un cierto dominio D.
S tiene plano tangente en un punto (a,b,f(a,b)) de S si y
slo si la funcin f es diferenciable en el punto (a,b).
La ecuacin del plano tangente a S en el punto
(a,b,f(a,b)) es
f f
z (a,b) (x a) (a,b) (y b) f(a,b)
x y
( (
= + +
( (


Ejemplo: Hallar la ecuacin del plano tangente al paraboloide elptico
de ecuacin en el punto (2,0,1)
6
y
4
x
z
2 2
+ =
f f
z (a,b) (x a) (a,b) (y b) f(a,b)
x y
( (
= + +
( (


0
3
y
) 0 , 2 (
y
f
1
2
x
) 0 , 2 (
x
f
) 0 , 2 (
) 0 , 2 (
=
(

(
=

=
(

(
=

Luego la ecuacin del plano es: z = 1(x-2)+0(y-0)+1

Es decir: z = x-1
DERIVADA DE LA FUNCIN COMPUESTA
REGLA DE LA CADENA
Sea z = f(u,v), donde u=u(x,y), y v=v(x,y).
Las derivadas parciales se pueden calcular haciendo la
sustitucin o bien con las siguientes frmulas:
f f u f v
x u x v x
f f u f v
y u y v y

= +


= +

Ejemplo 1: Dada la funcin
z = 2u sen v donde
Hallar
u = ln(xy)
v = xy
z z
y
x y


z f u f v 1
2senv. 2ucosv. y
x u x v x x
z f u f v 1
2senv. 2ucosv. x
y u y v y y

= + = +


= + = +

Ejemplo 2: Dada la funcin
z = x
2
y y
2
donde
Hallar cuando t=0
x = sent
y =e
t
dz
dt
2 t
dz z dx z dy
2xy.cost (x 2y)e
dt x dt y dt

= + = +

Para t=0 x = sen0 = 0 y= e
0
=1
y por tanto
t 0
dz
2
dt
=
(
=
(

Sean f :D
n
y un punto
perteneciente al interior de D
Definicin
Llamamos gradiente de f en el punto
y lo representamos por al vector definido por:
) p ,...., p , (p p
n 2 1
=
) p ,...., p , (p p
n 2 1
=
f(p)
1 2 n
f f f
f(p) (p), (p), , (p)
x x x
| |

=
|

\

GRADIENTE DE UNA FUNCIN

Sea f :D
n
, un punto
perteneciente al interior de D y un vector
Definicin
Llamamos derivada de f segn el vector en el punto
al lmite:
si existe.
Se representa
Si es un vector unitario, a este lmite se le llama
derivada direccional de f segn el vector en el punto
) p ,...., p , (p p
n 2 1
=
) p ,...., p , (p p
n 2 1
=
t 0
f(p tv) f(p)
lim
t

+
v
f
(p) =D f(p)
v

v
{ }
n
v 0
1 2 n
v (v , v , ,v ) =
v
p
Ejemplo: Hallar la derivada de la funcin
f(x,y,z)= x
2
z +x y en el punto (1,1,1) segn el vector
) 1 , 0 , 1 ( v =
t 0
t 0
2
t 0 t 0
3 2
t 0
f f(p tv) f(p)
(1,1,1) lim
v t
f[(1,1,1) t(1,0, 1)] f(1,1,1)
lim
t
f(1 t,1,1- t) 2 (1 t) (1 t) (1 t) 2
lim lim
t t
t 3t 4t
lim 4
t

+
= =

+
= =
+ + + +
= = =
+ +
= =
Sean f :D
2
y un punto perteneciente al
interior de D
Propiedades
El gradiente de f en el punto es ortogonal en a la curva de
nivel que pasa por ese punto
El vector gradiente define la direccin, el sentido y la
magnitud de la mxima pendiente, es decir, la direccin segn la cual
la derivada direccional es mxima
Las derivadas parciales son derivadas direccionales respecto a los
vectores de la base cannica
La derivada direccional se puede escribir como el producto escalar
del vector gradiente por un vector unitario
1 2
p (p ,p ) =
p
f(p)
p
v
v
D f(p) = f(p).v
1 2 n
1 2 n
f f f
= (p)v (p)v (p)v
x x x

+ + +

Definicin
Sean las funciones f
1
,f
2
,...,f
m
definidas de y
derivables en un punto de D
Se llama matriz jacobiana del sistema de funciones f
1
,f
2
,...,f
m
en
a la matriz de orden mxn
) p ,..., p , p ( p
n 2 1
=
p
1 1 1
1 2 n
2 2 2
1 2 m
1 2 n
1 2 n
p
m
m m
1 2 n
f f f
(p) (p) (p)
x x x
f f f
(p) (p) (p)
(f , f ,..., f )
x x x
(x , x ,..., x )
f
f f
(p) (p) (p)
x x x

| |
|

|
|

| |
|

=
|
|

\
|
|

|
| |

\

n
D
Ejemplo: Hallar la matriz jacobiana de las funciones
en el punto (1,2,1)
1 1 2 3 1 2 2 1 2 3 2 3
f (x ,x ,x ) x x ; f (x ,x ,x ) x 2x = =
|
|

\
|

=
|
|

\
|

=
=
|
|
|
|

\
|

=
2 1 0
0 1 2
) 1 , 2 , 1 (
2 1 0
0 x x
) 1 , 2 , 1 (
x
f
x
f
x
f
x
f
x
f
x
f
) 1 , 2 , 1 ( J
1 2
3
2
2
2
1
2
3
1
2
1
1
1
f
Ejemplo: Hallar el jacobiano del sistema de funciones {f,g} definidas
por:
f(x,y) = x
2
+y
2
, g(x,y) = x(1-y) en el punto (1, -1)
2 4 2
1 2
2 2
x y 1
y 2 x 2
y
g
x
g
y
f
x
f
) y , x (
) g , f (
Det
) 1 , 1 (
) 1 , 1 (
) 1 , 1 (
= + =

=
=

=

=
|
|

\
|

En particular, para m=n, la matriz jacobiana es cuadrada y

podemos hallar su determinante que se llama
jacobiano del sistema de funciones {f
1
,f
2
,...,f
n
} en
p
FUNCIONES IMPLCITAS
Definicin
Se dice que la ecuacin F(x,y,z)=0 define la funcin de dos variables
z=f(x,y) en un dominio si se cumple que
Proposicin Derivadas de primer orden
Sea F(x,y,z)=0
Derivando respecto a x
Derivando respecto a y

2
D

+ = = =

F
F F z f z F x
0 si 0
F
x z x x x z
z
= F(x, y,f(x, y)) 0 (x, y) D

+ = = =

F
F F z f z F x
0 si 0
F
y z y y y z
z
EXTREMOS DE FUNCIONES DE VARIAS VARIABLES
Sea f :D
n
y un punto
perteneciente a D
Definicin
f tiene un mximo local en D en el punto , si para todos
los puntos de un entorno de se verifica que
f tiene un mnimo local en D en el punto , si para todos los
puntos de un entorno de se verifica que
Los mximos y mnimos locales se llaman extremos locales.
) p ,...., p , (p p
n 2 1
=
x p
p
) x ( f ) p ( f
p
x
p
) x ( f ) p ( f
Definicin
f tiene un mximo local estricto en D en el punto , si para todos
los puntos de un entorno de tales que se verifica que
f tiene un mnimo local estricto en D en el punto , si para todos
los puntos de un entorno de tales que se verifica que
Los mximos y mnimos locales estrictos se llaman extremos locales
estrictos.
x p
p
) x ( f ) p ( f >
p
x p
) x ( f ) p ( f <
p x
p x
Sea f :D
n
y D
Definicin
f tiene un mximo global o absoluto en D en el punto
si se verifica que
f tiene un mnimo global o absoluto en D en el punto
si se verifica que
Proposicin
Si f es continua en un compacto (cerrado y acotado) D
entonces f alcanza un mximo global y un mnimo global en D.
Se pueden alcanzar en ms de un punto
) p ,...., p , (p p
n 2 1
=
p
) x ( f ) p ( f
p
) x ( f ) p ( f
x D
x D
Proposicin
Sea f una funcin derivable en un punto
Si es un extremo local de f entonces,
Es decir, para que haya un mximo o un mnimo local en un
punto es necesario que en ese punto se anulen todas
las derivadas parciales
Esta condicin no es suficiente
p
p
p
0 ) p ( f =
1 2 n
f f f
(p) 0 (p) 0 (p) 0
x x x

= = =

Definicin
Sea f una funcin derivable en D
Se llaman puntos crticos o estacionarios de f en D los
puntos que verifican la condicin
Definicin
Se llama punto de silla a un punto crtico de f que no es
un mximo ni un mnimo local de f
p
0 ) p ( f =
Definicin
Sea f de clase C
2
en un entorno de un punto interior
La matriz :
de orden nxn se llama matriz hessiana de f en p
2 2 2
2
1 2 1 n
1
2 2 2
2
p 2 1 2 n
2
2 2 2
2
n 1 n 2
n
f f f
(p) (p) (p)
x x x x
x
f f f
(p) (p) (p)
H(f ) x x x x
x
f f f
(p) (p) (p)
x x x x
x
| |

|

|
|

|
|
=

|
|
|

|
|


\

p D
Los n determinantes
para j=1,2,...,n se llaman menores preferentes de la
matriz hessiana
p
H(f )
2 2 2
2
1 2 1 j
1
2 2 2
2
2 1 2 j j
2
2 2 2
2
j 1 j 2
j
f f f
(p) (p) (p)
x x x x
x
f f f
(p) (p) (p)
x x x x H
x
f f f
(p) (p) (p)
x x x x
x

Proposicin
Sea f de clase C
2
en un entorno de un punto crtico
1) Si para j =1,2,...,n, se cumple que H
j
< 0 si j es impar y
H
j
>0 si j es par, entonces es un mximo local
2) Si H
j
> 0 para j =1,2,...,n, entonces es un mnimo
local
3) Si H
n
0 y no se cumple ninguno de los dos
apartados anteriores, entonces es un punto de silla
Para n=2
1) H
1
< 0 y H
2
> 0 Mximo local
2) H
1
> 0 y H
2
> 0 Mnimo local
3) H
2
< 0 Punto de silla
p
p
p
p
EXTREMOS DE FUNCIONES DE VARIAS VARIABLES
CONDICIONADOS
Sea f :D
n
, las m funciones f
1
,f
2
,...,f
m
( m < n ) definidas en D
y un punto solucin del sistema:
Definicin
f tiene un mximo local condicionado por el sistema de ecuaciones (1)
en el punto si para todos los puntos de un entorno de se
verifica que
f tiene un mnimo local condicionado por el sistema de ecuaciones (1)
en el punto si para todos los puntos de un entorno de se
verifica que
) p ,...., p , (p p
n 2 1
=
x
p
p
) x ( f ) p ( f
p
x
p
) x ( f ) p ( f
1 1 2 n
2 1 2 n
m 1 2 n
f (x , x , , x ) 0
f (x , x , , x ) 0
(1)
f (x , x , , x ) 0
=

ligaduras
Formamos la funcin auxiliar
y la matriz:
1 1 1
1 2 n
2 2 2
1 2 n
m m m
1 2 n
f f f
x x x
f f f
x x x A
f f f
x x x

| |
|

|
|

|
=
|
|
|

|
|

\

Los coeficientes l
1
, l
2
,...,l
m
son parmetros que hay que hallar y
se llaman multiplicadores de Lagrange
1 1 2 2 m m
h(x) f(x) f (x) f (x) f (x) x D = + + + +
Proposicin
Supongamos que las funciones f,f
1
,f
2
,...,f
m
son de clase C
1
en un conjunto abierto D
n
y consideremos un punto
de S tal que la matriz A evaluada en el punto sea de
rango fila completo (es decir, rango(A)=m).
Entonces, si es un extremo local de f, condicionado
por el sistema de ecuaciones (1), resulta que existen
1
,

2
,...,
m
nicos tales que la funcin auxiliar h tiene en
un punto crtico.
p
p
p
p
Es decir, para hallar los extremos condicionados de f
tenemos que hallar los multiplicadores de Lagrange y
los puntos crticos de la funcin auxiliar h teniendo
tambin en cuenta las ligaduras
Son mximos o mnimos?
1 1 1
1 2 n
2 2 2
1 2 n
m m m
1 2 n
2 2 2
1 2 m
2
1 1 1 1 2 1 n
1
2 2 2
1 2 m
2
2 2 2 2 1
2
f f f
0 0 0
x x x
f f f
0 0 0
x x x
f f f
0 0 0
x x x
B
f f f h h h
x x x x x x x
x
f f f h h h
x x x x x
x
... ...
... ...
... ... ... ... ... ... ... ...
... ...
... ...
... ...






=

2 n
2 2 2
1 2 m
2
n n n n 1 n 2
n
x x
f f f h h h
x x x x x x x
x
... ... ... ... ... ... ... ...
... ...
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|

|
|


\
Definicin Si f, f
1
,f
2
,...,f
m
son de clase C
2
en D, la matriz:
se llama matriz hessiana orlada
A
A
T
H
Proposicin
Consideremos la matriz hessiana orlada B evaluada en un
punto crtico de la funcin auxiliar h con los
multiplicadores de Lagrange obtenidos anteriormente
p
1) Si los ltimos n-m menores preferentes de la matriz B
tienen como signo (-1)
m
, resulta que la funcin f tiene un
mnimo local en el punto condicionado por el sistema de
ecuaciones (1).
2) Si los ltimos n-m menores preferentes de la matriz B
alternan su signo comenzando por el signo (-1)
m+1
, resulta
que la funcin f tiene un mximo local en el punto
condicionado por el sistema de ecuaciones (1).
p
p
Para n=2
Proposicin
f:
2
y hay una nica ligadura dada por la ecuacin
f
1
(x,y)=0, la funcin auxiliar es h = f+f
1
y la matriz
hessiana orlada queda:
1 1
1 2
2 2
1
2
1 1 2
1
2 2
1
2
2 2 1
2
f f
0
x x
f h h
B
x x x
x
f h h
x x x
x
| |

|

|
|

|
=
|

|
|
|
|


\
Evaluamos B en un punto crtico. Entonces:
1) Si |B|<0 la funcin f tiene un mnimo local condicionado
en ese punto
2) Si |B|>0 la funcin f tiene un mximo local condicionado
en ese punto