8/3/2009

1
Lecture 5: Theory of the Consumer:
Choice
Optimal choice
Consumer demand
Examples of demand
Utility functions from demand
functions
Implications of the MRS condition
An application: Taxes
Formal derivation of demand curves
8/3/2009
2
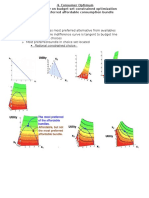
Object: find the bundle in the budget set that is on
the highest indifference curve
The bundle on the highest indifference curve that
just touches the budget line is labeled .
This is the optimal choice for the consumer.
It is the best bundle that she can afford, although
there are other bundles that she prefers.
See the following diagrams
) , (
*
2
*
1
x x
x
1
x
2
8/3/2009
3
x
1
x
2
Utility
Utility
x
2
x
1
8/3/2009
4
x
1
x
2
Utility
Utility
x
1
x
2
8/3/2009
5
Utility
x
1
x
2
Utility
x
1
x
2
8/3/2009
6
Utility
x
1
x
2
Utility
x
1
x
2
Affordable, but not
the most preferred
affordable bundle.
8/3/2009
7
x
1
x
2
Utility
Affordable, but not
the most preferred
affordable bundle.
The most preferred
of the affordable
bundles.
x
1
x
2
Utility
8/3/2009
8
Utility
x
1
x
2
Utility
x
1
x
2
8/3/2009
9
Utility
x
1
x
2
x
1
x
2
8/3/2009
10
x
1
x
2
Affordable
bundles
x
1
x
2
Affordable
bundles
8/3/2009
11
x
1
x
2
Affordable
bundles
More preferred
bundles
Affordable
bundles
x
1
x
2
More preferred
bundles
8/3/2009
12
x
1
x
2
x
1
*
x
2
*
x
1
x
2
x
1
*
x
2
*
(x
1
*,x
2
*) is the most
preferred affordable
bundle.
8/3/2009
13
At this choice, the indifference curve is tangent to
the budget line.
Tangency condition doesnt hold for all cases, but it
does hold for the more interesting cases.
What is always true is that at the optimal point, the
indifference curve cant cross the budget line
Exception: boundary optimum
8/3/2009
14
In general, tangency condition is only a
necessary condition for optimality.
It is not a sufficient condition as indicated in the
case of bent indifference curves or curves with
convex and nonconvex parts. Fig 5.4
Tangency condition of the budget line and
indifference curve is sufficient in the case of
convex preferences.
In general, there may be more than one bundle
that satisfies the tangency condition. However,
for strictly convex preferences (i.e., no flat spots
on IC), there is only one optimal choice on each
budget line.
7
8/3/2009
15
When x
1
* > 0 and x
2
* > 0 the optimal choice
bundle is INTERIOR.
If buying (x
1
*,x
2
*) costs P m then the budget
is exhausted.
x
1
x
2
x
1
*
x
2
*
(x
1
*,x
2
*) is interior .
(a) (x
1
*,x
2
*) exhausts the
budget; p
1
x
1
* + p
2
x
2
* = m.
(b) The slope of the indiff.
curve at (x
1
*,x
2
*) equals
the slope of the budget
constraint.
8/3/2009
16
(x
1
*,x
2
*) satisfies two conditions:
(a) the budget is exhausted;
p
1
x
1
* + p
2
x
2
* = m
(b) the slope of the budget constraint, -
p
1
/p
2
, and the slope of the indifference
curve, the MRS, containing (x
1
*,x
2
*) are
equal at (x
1
*,x
2
*).
Economic interpretation of the tangency condition:
MRS - as a rate of exchange where the consumer is just
willing to stay put.
Market is offering a rate of exchange equal to the ratio of
prices.
At equilibrium (optimal choice), the consumer must be at
a rate where MRS is equal to the rate of exchange.
If MRS is not equal to the price ratio, there could be some
scope for exchange of one good for another that is
affordable to the consumer.
Thus, whenever MRS is not equal to the price ratio, then
the consumer is not at the optimal choice.
8/3/2009
17
Demanded bundle or ordinary demand Optimal
choices of goods 1 and 2 at some set of prices and
income. It is the most preferred affordable bundle at the
given prices and budget.
Demand function Function that relates the optimal
choice, the quantity demanded to the different values of
prices and incomes
As prices and incomes change, the optimal bundle demanded
would also change.
Written as functions of both prices and income:
Different preferences lead to different demand functions
), , , (
), , , (
2 1 2
2 1 1
m p p x
m p p x
When x
1
* > 0 and x
2
* > 0 and (x
1
*,x
2
*)
exhausts the budget, and indifference curves
have no kinks, the ordinary demands are
obtained by solving:
(a) p
1
x
1
* + p
2
x
2
* = y
(b) the slopes of the budget constraint, -
p
1
/p
2
, and of the indifference curve
containing (x
1
*,x
2
*) are equal at (x
1
*,x
2
*).
8/3/2009
18
Suppose that the consumer has Cobb-
Douglas preferences.
Then
MU
U
x
ax x
a b
1
1
1
1
2
= =

c
c
MU
U
x
bx x
a b
2
2
1 2
1
= =

c
c
b a
x x x U(x
2 1 2 1
) , =
So the MRS is
At (x
1
*,x
2
*), MRS = -p
1
/p
2
so
.
/
/
1
2
1
2 1
2
1
1
2
1
1
2
bx
ax
x bx
x ax
x U
x U
dx
dx
MRS
b a
b a
= = = =

c c
c c
= =
ax
bx
p
p
x
bp
ap
x
2
1
1
2
2
1
2
1
*
*
* *
.
(A)
8/3/2009
19
(x
1
*,x
2
*) also exhausts the budget so
p x p x m
1 1 2 2
* *
. + =
(B)
So now we know that
*
1
2
1
*
2
x
ap
bp
x =
(A)
p x p x m
1 1 2 2
* *
. + =
(B)
8/3/2009
20
So now we know that
x
bp
ap
x
2
1
2
1
* *
=
(A)
p x p x m
1 1 2 2
* *
. + =
(B)
Substitute
So now we know that
x
bp
ap
x
2
1
2
1
* *
=
(A)
p x p x m
1 1 2 2
* *
. + =
(B)
p x p
bp
ap
x m
1 1 2
1
2
1
* *
. + =
Substitute
and get
This simplifies to .
8/3/2009
21
x
bm
a b p
2
2
*
( )
. =
+
Substituting for x
1
* in
p x p x m
1 1 2 2
* *
+ =
then gives
x
am
a b p
1
1
*
( )
. =
+
So we have discovered that the most preferred affordable
bundle for a consumer with Cobb-Douglas preferences
U x x x x
a b
( , )
1 2 1 2
=
is
( , )
( )
,
( )
.
* *
( ) x x
am
a b p
bm
a b p
1 2
1 2
=
+ +
8/3/2009
22
x
1
x
2
x
am
a b p
1
1
*
( )
=
+
x
bm
a b p
2
2
*
( )
=
+
b a
x x x x U
2 1 2 1
) , ( =
Property of the Cobb-Douglas - consumer always spends a
fixed fraction of his income on each good.
The size of the fraction depends on the exponents of the
function.
fraction spent on good 1:
substituting the demand function for good 1:
the same is true for good 2
This is why it is often convenient to represent the
exponents of the C-D function as equal to one.
m x p /
1 1
b a
a
p
m
b a
a
m
p
m
x p
+
=
+
=
1
1 1 1
8/3/2009
23
If either x
1
* = 0 or x
2
* = 0 then the ordinary
demand (x
1
*,x
2
*) is at a corner solution to
the problem of maximizing utility subject to
a budget constraint.
For instance, the demand for perfect
substitutes
Perfect substitutes
A consumer will purchase the cheaper one. If
they have the same price, then the consumer
doesnt care which one he purchases.
Demand function for good 1:

. when , 0
; when , m/p and 0 between no. any
; when , /
2 1
2 1 1
2 1 1
1

>
=
<
=
p p
p p
p p p m
x
8/3/2009
24
x
1
x
2
MRS = -1
x
1
x
2
MRS = -1
Slope = -p
1
/p
2
with p
1
> p
2
.
8/3/2009
25
x
1
x
2
MRS = -1
Slope = -p
1
/p
2
with p
1
> p
2
.
x
1
x
2
2
*
2
p
y
x =
0
*
1
= x
MRS = -1
Slope = -p
1
/p
2
with p
1
> p
2
.
8/3/2009
26
x
1
x
2
x
y
p
1
1
*
=
x
2
0
*
=
MRS = -1
Slope = -p
1
/p
2
with p
1
< p
2
.
So when U(x
1
,x
2
) = x
1
+ x
2
, the most
preferred affordable bundle is (x
1
*,x
2
*)
where
|
|
.
|

\
|
= 0 , ) , (
1
*
2
*
1
p
y
x x
and
|
|
.
|

\
|
=
2
*
2
*
1
, 0 ) , (
p
y
x x
if p
1
< p
2
if p
1
> p
2
.
8/3/2009
27
x
1
x
2
MRS = -1
Slope = -p
1
/p
2
with p
1
= p
2
.
y
p
1
y
p
2
x
1
x
2
All the bundles in the
constraint are equally the
most preferred affordable
when p
1
= p
2
.
y
p
2
y
p
1
8/3/2009
28
Perfect Complements: Optimal choice would always lie
on the diagonal, no matter what the prices are.
No matter what the prices, consumer is purchasing the
same amount of good 1 for each good 2 (or at the fixed rate
at which they complement one another).
Adding the budget constraint to this condition and solving
algebraically just gives us the optimal choice bundle.
it is as if the consumer were just spending all of her money
on a single good that has a combined price.
) /(
2 1 2 1
2 2 1 1
p p m x x x
m x p x p
+ = = =
= +
x
1
x
2
U(x
1
,x
2
) = min{ax
1
,x
2
}
x
2
= ax
1
8/3/2009
29
x
1
x
2
MRS = 0
U(x
1
,x
2
) = min{ax
1
,x
2
}
x
2
= ax
1
x
1
x
2
MRS = -

MRS = 0
U(x
1
,x
2
) = min{ax
1
,x
2
}
x
2
= ax
1
8/3/2009
30
x
1
x
2
MRS = -

MRS = 0
MRS is undefined
U(x
1
,x
2
) = min{ax
1
,x
2
}
x
2
= ax
1
x
1
x
2
U(x
1
,x
2
) = min{ax
1
,x
2
}
x
2
= ax
1
8/3/2009
31
x
1
x
2
U(x
1
,x
2
) = min{ax
1
,x
2
}
x
2
= ax
1
Which is the most
preferred affordable bundle?
x
1
x
2
U(x
1
,x
2
) = min{ax
1
,x
2
}
x
2
= ax
1
The most preferred
affordable bundle
8/3/2009
32
x
1
x
2
U(x
1
,x
2
) = min{ax
1
,x
2
}
x
2
= ax
1
x
1
*
x
2
*
x
1
x
2
U(x
1
,x
2
) = min{ax
1
,x
2
}
x
2
= ax
1
x
1
*
x
2
*
(a) p
1
x
1
* + p
2
x
2
* = m
8/3/2009
33
x
1
x
2
U(x
1
,x
2
) = min{ax
1
,x
2
}
x
2
= ax
1
x
1
*
x
2
*
(a) p
1
x
1
* + p
2
x
2
* = m
(b) x
2
* = ax
1
*
(a) p
1
x
1
* + p
2
x
2
* = m; (b) x
2
* = ax
1
*.
Substitution from (b) for x
2
* in (a) gives p
1
x
1
* + p
2
ax
1
* = m
which gives
A bundle of 1 commodity 1 unit and a commodity 2 units costs p
1
+ ap
2
;
m/(p
1
+ ap
2
) such bundles are affordable.
.
ap p
am
x ;
ap p
m
x
2 1
*
2
2 1
*
1
+
=
+
=
8/3/2009
34
x
1
x
2
U(x
1
,x
2
) = min{ax
1
,x
2
}
x
2
= ax
1
x
m
p ap
1
1 2
*
=
+
x
am
p ap
2
1 2
*
=
+
Discrete goods
good 1 - is a discrete good
good 2 is money spent on everything else
To look at optimal choice, two ways:
compare the bundles (1, m-p
1
), (2, m-2p
1
), (3,
m-3p
1
) and get the one which yields the highest
utility
Indifference curve analysis: Typically, as the
price decreases further, the consumer will
choose to consume more units of good 1.
8/3/2009
35
Concave Preferences
Optimal choice would be a boundary choice.
Non-convex preferences imply that if you dont
like to consume two things together (the
opposite of convex preferences), then youll
spend all of your money on one or the other
8/3/2009
36
x
1
x
2
x
1
x
2
8/3/2009
37
x
1
x
2
The most preferred
affordable bundle
Notice that the tangency solution
is not the most preferred affordable
bundle.
Neutrals and Bads
Neutral good - Consumer spends all her money
on the good she likes and doesnt purchase any
of the neutral good.
Bad - Consumer spends all her money on the
good.
8/3/2009
38
Using observed demand behavior, can we determine the kind of
preferences that generated that demand?
Example: A Cobb-Douglas utility function may be inferred if
demand behavior shows a certain constancy in the shares of
expenditures for each good
We can use this fitted utility function to analyze the effects of
policy changes.
In general:
Given observations of choice behavior, we try to determine
what is maximized.
After determining this, we predict choice behavior in new
situations and or evaluate proposed changes in the economic
environment.
Analysis can be extended by estimating preferences for certain
groups of individuals and analyzing differential impact of policy
changes on them.
If everyone is facing the roughly the same
prices for two goods and everyone is
optimizing and at an interior solution, then
everyone must have the same marginal rates
of substitution for the two goods.
The quantities consumed would differ
At quantities consumed however, the MRS
would be the same.
8/3/2009
39
Price ratios can be used to value possible
changes in consumption bundles.
Since prices measure the rate at which
people are just willing to substitute one
good for another, they can be used to value
policy proposals that involve making
changes in consumption.
If the government wants to raise a certain amount of
revenue, is it better to impose a quantity tax or an
income tax?
Budget constraint with the quantity tax:
Optimal choice should satisfy the budget
constraint:
The revenue raised by the tax is:
m x p x t p = + +
2 2 1 1
) (
m x p x t p = + +
*
2
*
1
2 1
) (
*
1
*
tx R =
8/3/2009
40
Budget constraint with the income tax:
substituting for R* :
This budget line has the same slope but will pass through
the point .
It is therefore an affordable choice for the consumer
*
2 2 1 1
R m x p x p = +
*
2 2 1 1
1
tx m x p x p = +
) , (
*
2
*
1
x x
However is not an optimal choice
with the income tax.
With the quantity tax, the MRS is
Income tax allows us to trade at
Income tax budget line cuts the indifference
curve at the optimal choices with the quantity
taxes, implying that there will be a point in the
budget line that will be preferred to it.
) , (
*
2
*
1
x x
2 1
/ ) ( p t p +
2 1
/ p p
8/3/2009
41
Therefore , an income tax is definitely better
than the quantity tax since you can raise the
same amount of revenue while leaving the
consumers better off.
8/3/2009
42
Limitations:
Assume only one consumer.
Assume that consumers income doesnt
change after the imposition of the tax, i.e.,
his income generating behavior doesnt
change.
Ignored the supply response.
Ways to derive the demand
curves:
By using MRS condition and the
budget constraint
By unconstrained maximization
By constrained maximization
8/3/2009
43
MRS condition and the budget constraint
Represent the consumers preferences by a
utility function :
Optimal choice must satisfy the condition
MRS can be expressed as the negative of the
ratio of derivatives of the utility function.
Substituting and canceling the minus signs :
) , (
2 1
x x u
2
1
2 1
) , (
p
p
x x MRS =
2
1
2 2 1
1 2 1
/ ) , (
/ ) , (
p
p
x x x u
x x x u
=
c c
c c
Optimal choices should also satisfy the budget constraint:
These give two equations in two unknowns, which can be solved.
One way is to express the budget constraint in terms of one of
the goods and substitute the definition into the MRS condition.
substituting into equation we get:
This has just one unknown variable x
1
, and can be solved for as a
function of the prices and income. The budget constraint then
yields the solution for x
2
as function of prices and income
m x p x p = +
2 2 1 1
1
2
1
2
2
x
p
p
p
m
x =
2
1
2 1 2 1 2 1
1 1 2 1 2 1
/ ) ) / ( / , (
/ ) ) / ( / , (
p
p
x x p p p m x u
x x p p p m x u
=
c c
c c
8/3/2009
44
Unconstrained maximization
i)
Unconstrained equivalent: define one variable in terms of the
other
ii)
Substitute in the utility function to get the unconstrained max
problem
iii)
m x p x p
x x u
= +
2 2 1 1
2 1
such that
) , ( max
1
2
1
2
1 2
) ( x
p
p
p
m
x x =
) ) / ( / , ( max
1 2 1 2 1
x p p p m x u
Differentiate with respect to x
1
, set the result equal to zero to
derive the first order condition of the form:
iv)
Differentiating equation in (ii) yields
v)
Substituting into (iv) gives us
Utilizing the condition that the optimal choice must satisfy the
budget constraint gives us two equations in two unknowns
0
)) ( , ( )) ( , (
1
2
2
1 2 1
1
1 2 1
=
c
c
+
c
c
dx
dx
x
x x x u
x
x x x u
2
1
1
2
p
p
dx
dx
=
2
1
2
* *
1
* *
/ ) , (
/ ) , (
2 1
2 1
p
p
x x x u
x x x u
=
c c
c c
8/3/2009
45
Constrained maximization
Construct the Lagrangian function:
Differentiate to get the first order conditions:
Solve the three equations in three unknowns by matrix algebra
). ( ) , (
2 2 1 1 2 1
m x p x p x x u L + =
. 0
0
) , (
0
) , (
2 2 1 1
2
2
*
2
*
1
2
1
1
*
2
*
1
1
= + =
c
c
=
c
c
=
c
c
=
c
c
=
c
c
m x p x p
L
p
x
x x u
x
L
p
x
x x u
x
L

Or reduce the equations by noting that:

This equation simply says that the MRS must equal the price
ratio.
The budget constraint gives us the other equation so we are back
to two equations in two unknowns
2
1
2
*
2
*
1
1
*
2
*
1
) , (
) , (
p
p
x
x x u
x
x x u
=
c
c
c
c