Documenti di Didattica
Documenti di Professioni
Documenti di Cultura
Polphys-Ss11 Problems1
Caricato da
Edward Begbaunimushuye ApebendeDescrizione originale:
Titolo originale
Copyright
Formati disponibili
Condividi questo documento
Condividi o incorpora il documento
Hai trovato utile questo documento?
Questo contenuto è inappropriato?
Segnala questo documentoCopyright:
Formati disponibili
Polphys-Ss11 Problems1
Caricato da
Edward Begbaunimushuye ApebendeCopyright:
Formati disponibili
Problem Set 1
Introduction to Polymer Physics, SS 2011, 13.4.10
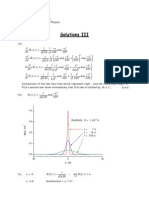
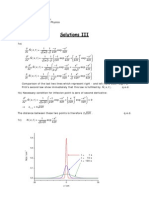
1. Using two polystyrene fractions with very uniform molecular weight distribution (P 1), a bimodal mixture with a mass average molecular weight of Mw = 25000 g/mol and a polydispersity of P = 1.25 should be prepared. The mixture should contain equal numbers of the different chains. Calculate the molecular weight and the number average degree of polymerization of the two components. 2. Step-growth polymerization. (a) Using the equations given in the lecture, prove that the number and weight average 1 degrees of polymerization are given by Nn = 1x (Carothers equation) and Nw = 1+x , 1x respectively (x is the extent of reaction). (b) Comment on the behavior of Nn for x 1. In how far does this make sense physically? What would rather happen in a real system? Why is it hardly possible to ever achieve x = 1, i.e, what are the factors that limit the molecular weight in step-growth reactions? 3. Explain why the intensity of light scattered by a polymer solution depends on the second virial coefcient (A2 ) of the solution. The central argument rests on a question of length scales: How does the wavelength of visible light compare to the average distance between coils (estimate this for a polystyrene solution with Mn = 105 g/mol at 1 g/l, assuming e.g. a cubic arrangement)? Would the polymer fraction (as compared to the pure solvent) scatter any appreciable excess amount of light if the molecules were xed at their positions?
Potrebbero piacerti anche
- Macromolecular Microsymposium — 16: Main Lectures Presented at the Sixteenth Microsymposium on Macromolecules (Advances in Scattering Methods), Prague, 12 - 16 July 1976Da EverandMacromolecular Microsymposium — 16: Main Lectures Presented at the Sixteenth Microsymposium on Macromolecules (Advances in Scattering Methods), Prague, 12 - 16 July 1976B. SedláčekNessuna valutazione finora
- A unitary theory of nuclear, electromagnetic and gravitational fields: Einsteins Dream, Unified Fields TheoryDa EverandA unitary theory of nuclear, electromagnetic and gravitational fields: Einsteins Dream, Unified Fields TheoryNessuna valutazione finora
- Physico-Chemistry of Solid-Gas Interfaces: Concepts and Methodology for Gas Sensor DevelopmentDa EverandPhysico-Chemistry of Solid-Gas Interfaces: Concepts and Methodology for Gas Sensor DevelopmentNessuna valutazione finora
- Physical Chemistry of Polyelectrolyte SolutionsDa EverandPhysical Chemistry of Polyelectrolyte SolutionsMitsuru NagasawaNessuna valutazione finora
- Nuclear Techniques in Analytical Chemistry: International Series of Monographs on Analytical ChemistryDa EverandNuclear Techniques in Analytical Chemistry: International Series of Monographs on Analytical ChemistryNessuna valutazione finora
- Problems in Quantum Mechanics: Third EditionDa EverandProblems in Quantum Mechanics: Third EditionValutazione: 3 su 5 stelle3/5 (2)
- Power Geometry in Algebraic and Differential EquationsDa EverandPower Geometry in Algebraic and Differential EquationsNessuna valutazione finora
- Reactive Oxygen Species: Signaling Between Hierarchical Levels in PlantsDa EverandReactive Oxygen Species: Signaling Between Hierarchical Levels in PlantsFranz-Josef SchmittNessuna valutazione finora
- Few body dynamicsDa EverandFew body dynamicsAsoke MitraNessuna valutazione finora
- Nuclear, Particle and Many Body PhysicsDa EverandNuclear, Particle and Many Body PhysicsPhilip MorseNessuna valutazione finora
- Interacting Macromolecules: The Theory and Practice of Their Electrophoresis, Ultracentrifugation, and ChromatographyDa EverandInteracting Macromolecules: The Theory and Practice of Their Electrophoresis, Ultracentrifugation, and ChromatographyNessuna valutazione finora
- Introduction to Non-Linear Mechanics. (AM-11), Volume 11Da EverandIntroduction to Non-Linear Mechanics. (AM-11), Volume 11Nessuna valutazione finora
- Collection of Problems in Classical Mechanics: International Series of Monographs in Natural PhilosophyDa EverandCollection of Problems in Classical Mechanics: International Series of Monographs in Natural PhilosophyValutazione: 3 su 5 stelle3/5 (2)
- Theoretical Chemistry Advances and Perspectives V2Da EverandTheoretical Chemistry Advances and Perspectives V2Henry EyringNessuna valutazione finora
- Reviews in Computational ChemistryDa EverandReviews in Computational ChemistryAbby L. ParrillNessuna valutazione finora
- Tetrahedron Reports on Organic Chemistry: Volume 3.21-30Da EverandTetrahedron Reports on Organic Chemistry: Volume 3.21-30Derek BartonNessuna valutazione finora
- Elementary Particle Physics in a NutshellDa EverandElementary Particle Physics in a NutshellValutazione: 4.5 su 5 stelle4.5/5 (3)
- Interactions between Electromagnetic Fields and Matter: Vieweg Tracts in Pure and Applied PhysicsDa EverandInteractions between Electromagnetic Fields and Matter: Vieweg Tracts in Pure and Applied PhysicsNessuna valutazione finora
- Quantitative Human Physiology: An IntroductionDa EverandQuantitative Human Physiology: An IntroductionValutazione: 2 su 5 stelle2/5 (1)
- Stereoelectronic Effects: A Bridge Between Structure and ReactivityDa EverandStereoelectronic Effects: A Bridge Between Structure and ReactivityNessuna valutazione finora
- Multivalency: Concepts, Research and ApplicationsDa EverandMultivalency: Concepts, Research and ApplicationsJurriaan HuskensNessuna valutazione finora
- Ideas of Quantum Chemistry: Volume 2: InteractionsDa EverandIdeas of Quantum Chemistry: Volume 2: InteractionsValutazione: 4 su 5 stelle4/5 (1)
- Advances in Structure Research by Diffraction Methods: Fortschritte der Strukturforschung mit BeugungsmethodenDa EverandAdvances in Structure Research by Diffraction Methods: Fortschritte der Strukturforschung mit BeugungsmethodenR. BrillNessuna valutazione finora
- Elementary Reactor Physics: The Commonwealth and International Library: Nuclear Engineering DivisionDa EverandElementary Reactor Physics: The Commonwealth and International Library: Nuclear Engineering DivisionNessuna valutazione finora
- Generalized van der Waals Theory of Molecular Fluids in Bulk and at SurfacesDa EverandGeneralized van der Waals Theory of Molecular Fluids in Bulk and at SurfacesNessuna valutazione finora
- Reaction Kinetics: Reactions in SolutionDa EverandReaction Kinetics: Reactions in SolutionValutazione: 3.5 su 5 stelle3.5/5 (4)
- Measurements and Time Reversal in Objective Quantum Theory: International Series in Natural PhilosophyDa EverandMeasurements and Time Reversal in Objective Quantum Theory: International Series in Natural PhilosophyNessuna valutazione finora
- Green's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)Da EverandGreen's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)Nessuna valutazione finora
- Bioreactor Modeling: Interactions between Hydrodynamics and BiologyDa EverandBioreactor Modeling: Interactions between Hydrodynamics and BiologyNessuna valutazione finora
- Universal RAFT Agents Enable Block Copolymer SynthesisDocumento2 pagineUniversal RAFT Agents Enable Block Copolymer SynthesisEdward Begbaunimushuye ApebendeNessuna valutazione finora
- LSG PmPhys3Documento2 pagineLSG PmPhys3Edward Begbaunimushuye ApebendeNessuna valutazione finora
- LSG PmPhys3Documento2 pagineLSG PmPhys3Edward Begbaunimushuye ApebendeNessuna valutazione finora
- Sunthar Polymer RheologyDocumento21 pagineSunthar Polymer RheologyPuli IlupNessuna valutazione finora