AE 5332 Conformal Mapping Conformal mapping is a mathematical technique used to convert (or map) one mathematical problem and

solution into another. Formally, a conformal mapping is a transformation w = f(z) that preserves local angles. The function mapping is between domains in the complex plane. More formally, a map, f : u v is conformal at u0 if it preserves oriented angles between curves through u0 with respect to their orientation.
This figure shows a rectangular grid (top) and its image under a conformal map f (bottom). It is seen that f maps pairs of lines intersecting at 90 to pairs of curves still intersecting at 90

An analytic function is conformal at any point where it has a nonzero derivative. Conversely, any conformal mapping of a complex variable which has continuous partial derivatives is analytic. Conformal mapping is extremely important in complex analysis, as well as in many areas of physics and engineering. A conformal mapping is also known as conformal map, conformal transformation, angle-preserving transformation, or biholomorphic map.

Conformal maps preserve both angles and the shapes of infinitesimally small figures, but not necessarily their size. The conformal property may be described in terms of the Jacobian derivative matrix of a coordinate transformation. If the Jacobian matrix of the transformation is everywhere a scalar times a rotation matrix, then the transformation is conformal.

Applications If a function is harmonic (that is, it satisfies Laplace's equation ) over a particular space, and is transformed via a conformal map to another space, the transformation is also harmonic. For this reason, any function which is defined by a potential can be transformed by a conformal map and still remain governed by a potential.

Conformal mapping is a short cut to the solution of the Laplace's equation, used in a limited group of engineering problems. The problem has to be 2D (two dimensional), i.e., the boundaries, boundary conditions and sources contain only two variables, x and y.

Examples of equations defined by a potential include the electromagnetic field, the gravitational field, and, in fluid dynamics, potential flow, which is an approximation to fluid flow assuming constant density, zero viscosity, and irrotational flow. One example of a fluid dynamic application of a conformal map is the Joukowsky transform. Conformal mappings are invaluable for solving problems in engineering and physics that can be expressed in terms of functions of a complex variable but that exhibit inconvenient geometries. By choosing an appropriate mapping, the analyst can transform the inconvenient geometry into a much more convenient one. For example, one may wish to calculate the electric field, arising from a point charge located near the corner of two conducting planes separated by a certain angle (where z is the complex coordinate of a point in 2-space). This problem per se is quite clumsy to solve in closed form. However, by employing a very simple conformal mapping, the inconvenient angle is mapped to one of precisely radians, meaning that the corner of two planes is transformed to a straight line. In this new domain, the problem (that of calculating the electric field impressed by a point charge located near a conducting wall) is quite easy to solve. The solution is obtained in this domain, E(w), and then mapped back to the original domain by noting that w was obtained as a function (viz., the composition of E and w) of z whence E(w) can be viewed as E(w(z)) which is a function of the original coordinate basis. Note that this application is not a contradiction to the fact that conformal mappings preserve angles, they do so only for points in the interior of their domain, and not at the boundary. Many years ago, the Russian mathematician Joukowski developed a mapping function that converts a circular cylinder into a family of airfoil shapes (see figure below). If points in the cylinder plane are represented by the complex coordinates x for the horizontal and y for the vertical, then every point z is specified by: z = x + i y

Similarly, in the airfoil plane, the horizontal coordinate is B and the vertical coordinate is C, and every point A is specified by: A = B + i C Then Joukowski's mapping function that relates points in the airfoil plane to points in the cylinder plane is given in the red box: A = z + 1 / z

The mapping function also converts the entire flow field around the cylinder into the flow field around the airfoil. We know the velocity and pressures in the plane containing the cylinder. The mapping function gives us the velocity and pressures around the airfoil. Knowing the pressure around the airfoil, we can then compute the lift. Transformation of boundary conditions. Two types of boundary conditions remain unchanged by the transformation and problems with these boundary conditions are best suited for conformal mapping. The B.C. types are: 1) The value of a harmonic function is constant on the boundary (one type of Dirichlet problem) 2) The normal derivative of a harmonic function is zero on the boundary (one type of Neumann problem) (The conditions are that f and its inverse are analytical) Table of Conformal Maps A Table of Conformal Mappings is given in Appendix F of the textbook. For polygonal boundaries a general method of constructing the mapping is offered by Schwartz-Cristoffel transformations. For non-polygonal boundaries one must rely on "dictionaries" of mappings. One such dictionary with 30 different mappings is found in a student text book, Complex variables and applications by R. V. Churchill. Examples The following pages contain some worked out problems from the Department of Mathematics at the Hong Kong University http://www.math.ust.hk/

Worked examples Conformal mappings and bilinear transformations

Example 1 Suppose we wish to nd a bilinear transformation which maps the circle |z i| = 1 to the circle |w| = 2. Since |w/2| = 1, the linear transformation w = f (z) = 2z 2i, which magnies the rst circle, and translates its centre, is a suitable choice. (Note that there is no unique choice of bilinear transformation satisfying the given criteria.) Since f (i) = 0, f maps the inside of the rst circle to the inside of the second. Suppose now we wish to nd a bilinear transformation g which maps the inside of the rst circle to the outside of the second circle. Let g(z) = (z + )/(z + ). We choose g(i) = , so that g(z) = (z + )/(z i) without the loss of generality. Three points on the rst circle are 0, 1 + i and 2i, and g(0) = i, g(1 + i) = (1 + i) + and g(2i) = 2 i. All three of these points must lie on |w| = 2, so the simplest choice is = 0 and = 2. Then g(z) = 2/(z i). Suppose now we wish to nd a bilinear transformation h which maps the circle |z i| = 1 to the real line. Since 0, 1 + i and 2i lie on the given circle and the given line passes through 0, 1 and , we simply choose h so that h(0) = 0, h(1 + i) = 1 and h(2i) = say. Then h(z) = z/(iz + 2). Note that h(i) = i, so h maps the region given by |z 1| < 1 to the upper half-plane. This can be shown formally by letting z = x + iy. Then h(z) = and |z i| < 1 Example 2 Solution We are naturally led to look for a bilinear transformation that maps the circle |z| = 1 onto the imaginary axis. The transformation must therefore have a pole on the circle, according to our earlier remarks. Moreover, the origin w = 0 must also lie on the image of the circle. As a rst step, lets look at w = f1 (z) = which maps 1 to and 1 to 0. From the geometric properties of bilinear transformations, we can conclude that (i) maps |z| = 1 onto some straight line through the origin. To see which straight line, we plug in z = i and nd that the point w= i+1 = i i1 z+1 , z1 (i) 2x i[x2 + (y 1)2 1] x2 + (y 2)2

x2 + (y 1)2 < 1.

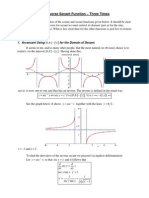
Find a conformal map of the unit disk |z| < 1 onto the right half-plane Re w > 0.

also lies on the line. Hence the image of the circle under f1 must be the imaginary axis. To see which half-plane is the image of the interior of the circle, we check the point z = 0. It is mapped by (i) to the point w = 1 in the left half-plane. This not what we want, but it can be corrected by a nal rotation of , yielding w = f (z) = z+1 1+z = z1 1z (ii)

as an answer to the problem. (Of course, any subsequent vertical translation or magnication can be permitted.)

Example 3 Find the image of the interior of the circle C : |z 2| = 2 under the bilinear transformation w = f (z) = z . 2z 8

Solution First we nd the image of the circle C. Since f has a pole at z = 4 and this point lies on C, the image has to be a straight line. To specify this line all we need is to determine two of its nite points. The points z = 0 and z = 2 + 2i which lie on C have, as their images, w = f (0) = 0 and w = f (2 + 2i) = 2 + 2i i = . 2(2 + 2i) i 2

Thus the image of C is the imaginary axis in the w-plane. From connectivity, we know that the interior of C is therefore mapped either onto the right half-plane Re w > 0 or onto the left half-plane Re w < 0. Since z = 2 lies inside C and w = f (2) = 2 1 = 48 2

lies in the left half-plane, we conclude that the image of the interior of C is the left half-plane.

Example 4 Find a bilinear transformation that maps the region D1 : |z| > 1 onto the region D2 : Re w < 0. Solution 2

We shall take both D1 and D2 to be left regions. This is accomplished for D1 by choosing any three points on the circle |z| = 1 that give it a negative (clockwise) orientation, say z1 = 1, Similarly the three points w1 = 0, w2 = i, w3 = z2 = i, z3 = 1.

on the imaginary axis make D2 it left region. Hence a solution to the problem is given by the transformation that takes 1 to 0, This we obtain by setting (w, 0, i, ) = (z, 1, i, 1), that is, w0 (z 1)(i + 1) = , i0 (z + 1)(i 1) which yields w= (z 1)(1 + i) 1z = . (z + 1)(i 1) 1+z i to i, 1 to .

Example 5 Mapping the unit disk onto an innite horizontal strip We will describe a sequence of analytic and one-to-one mappings that takes the unit circle onto an innite horizontal strip. The rst linear fractional transformation, w1 = i(z), is obtained by 1z multiplying by i the linear fractional transformation (z), where (z) = i maps the unit 1+z disk onto the upper half-plane, and multiplication by i rotates by the angle , the eect of 2 i(z) is to map the unit disk onto the right half-pane.

Figure The principal branch of the logarithm, Log z, maps the right half-plane onto an innite horizontal strip. In the gure, Log w1 = ln |w1 | + iArg w1 is the principal branch of the logarithm. As w1 varies in the right half-plane, Arg w1 varies between and , which explains the location of the horizontal 2 2 boundary of the innite strip. The desired mapping is w = f (z) = Log (i(z)) = Log 3 1z . 1+z

Example 6 Find a linear fractional transformation that maps the interior of the circle |z i| = 2 onto the exterior of the circle |w 1| = 3. We need only three points on the rst circle in clockwise order and three on the second circle in counterclockwise order. Let z1 = i, z2 = 2 + i, z3 = 3i and w1 = 4, w2 = 1 + 3i, w3 = 2. We have

(w 4)(3 + 3i) (z + i)(2 2i) = , (w + 2)(3 + 3i) (z 3i)(2 + 2i) which, when solved for w, denes the mapping w= z 7i . zi

The center of the circle, |z i| = 2, is z = i. Our transformation maps this point to w = , which is clearly in the exterior of the circle. |w 1| = 3. Example 7 Find a linear fractional transformation that maps the half-plane dened by Im (z) > Re (z) onto the interior of the circle |w 1| = 3. We shall regard the specied half-plane as the interior of the circle through dened by the line Im (z) = Re (z). As noted earlier, it is usually convenient to use when possible as a point on a line. Then three points in clockwise order are z1 = , z2 = 0, and z3 = 1 i. Three points on the circle, |w 1| = 3, in clockwise order are w1 = 1 + 3i, w2 = 4, w3 = 2. The unique linear fractional transformation mapping these points in order is dened by w= z + , z+

where from the images of and 0, we must have = 1 + 3i = 4, and from the image of z3 = 1 i, we must have (1 i) + = 2. (1 i) + By substituting = 4 into the preceding equation, we have = 4i and 4 = i,

so that w= (1 + 3i)z + 4i z+i

is the required linear fractional transformation. Now z0 = i is in the half-plane dened by Im (z) > Re (z). Its image under the transformation 5 3 3 3 3 is w0 = + i and as w0 1 = + i has a modulus of 2 2.12132 < 3, w0 is in the interior 2 2 2 2 2 of |w 1| = 3.